姜春濤

　?。ㄋ拇ù髮W(xué) 計(jì)算機(jī)學(xué)院，四川 成都 610000）

       摘要：利用霍夫變換進(jìn)行橢圓檢測,，需要尋找橢圓的參數(shù),。使用橢圓主半軸的長度，可以快速地尋找橢圓的參數(shù),。這種方法需要將橢圓的短半軸長度求解出來,，然后僅使用一維的聚集數(shù)組收集橢圓短半軸的長度信息。該方法不需要計(jì)算橢圓的邊的切線或者曲率,，因此不易受到噪聲的影響,。該方法的實(shí)現(xiàn)不需要大量的內(nèi)存。合成的圖像和真實(shí)的圖像測試表明,，這種方法是有效的,。

　　關(guān)鍵詞：圖像處理；霍夫變換,；橢圓檢測

　　中圖分類號(hào)：TP751文獻(xiàn)標(biāo)識(shí)碼：ADOI： 10.19358/j.issn.1674-7720.2017.04.013

　　引用格式：姜春濤.利用長軸檢測橢圓［J］.微型機(jī)與應(yīng)用,，2017,36（4）：43-46.

0引言

　　橢圓檢測是圖像處理中的一個(gè)重要的問題，已經(jīng)有很多種橢圓檢測的方法［110］,。完全定義一個(gè)橢圓需要五個(gè)參數(shù),，因此變化霍夫變換［11］進(jìn)行橢圓檢測需要五維的參數(shù)空間。這需要很大的內(nèi)存和時(shí)間,，所以需要使用幾何上的限制以減少參數(shù)空間,。為了減少橢圓檢測中時(shí)間和空間的需求，以前的技術(shù)大部分將 5 維的參數(shù)空間分為更少維數(shù)的子空間,。參考文獻(xiàn)［1］介紹了一種基于幾何屬性的橢圓檢測方法,。 參考文獻(xiàn)［2］通過在相同的水平和垂直位置上的邊緣點(diǎn)構(gòu)造兩個(gè)中間點(diǎn)矩陣，然后,，利用霍夫變換從這兩個(gè)矩陣中檢測出直線［1213］,，這些直線的交提供了可能的橢圓中心。 文獻(xiàn)［3］提出了一種包含切線信息的用于橢圓提取的映射方法。文獻(xiàn)［4］提出了一種有效的從圖像的邊中檢測橢圓的方法,，其思路是在霍夫變換基礎(chǔ)上從邊緣中檢測對稱軸,，一個(gè)高維的問題轉(zhuǎn)化成兩個(gè)二維的問題。先從邊緣中找到對稱軸,，然后從邊緣中找到橢圓,。文獻(xiàn)［4］介紹了一種利用橢圓長軸進(jìn)行橢圓檢測的方法。利用短半軸的長度獲取在同一橢圓上的點(diǎn),，然后橢圓的參數(shù)被計(jì)算出來,。

　　本文的橢圓檢測方法基于文獻(xiàn)［9］介紹的方法。這種方法使用新的方式計(jì)算橢圓的短半軸,，需要的運(yùn)算量稍微少一些,。對于給定的橢圓長軸的兩個(gè)端點(diǎn)，文中提供了一種用于減少計(jì)算短半軸長度的點(diǎn)數(shù)的方法,。

1橢圓參數(shù)的尋找

　　一個(gè)橢圓具有五個(gè)參數(shù),，它們分別是橢圓的中心坐標(biāo)O(x0,y0)、橢圓的長半軸a,、橢圓的短半軸b,、橢圓的長軸與x軸的夾角T。橢圓的五個(gè)參數(shù)如圖1所示,。

　　圖2是與圖1相對應(yīng)的橢圓,，它是將原橢圓的中心平移到坐標(biāo)原點(diǎn)，然后順時(shí)針旋轉(zhuǎn)角度T后得到的,。對應(yīng)于圖2的橢圓方程是:

　　其中a2－x2>0,。(2)

　　從圖1到圖2的線性變換，先是將橢圓的中心平移到坐標(biāo)原點(diǎn),，其對應(yīng)的變換矩陣為P,，然后將橢圓順時(shí)針旋轉(zhuǎn)角度T，其對應(yīng)的變換矩陣為R,。整個(gè)變換的復(fù)合矩陣為A［1415］。變換矩陣P,，T ,，R如下：

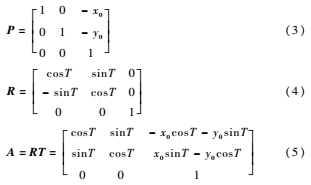
　　假設(shè)點(diǎn)B(x,y)是位于圖1橢圓上的一點(diǎn)，而點(diǎn)C(xt,yt)是位于圖2橢圓上由點(diǎn)B經(jīng)過線性變換A后的對應(yīng)點(diǎn),則C的坐標(biāo)為:

　　從式(8)和(9)中可以得到

　　a2>x2t(10)

　　x2t+y2t≤a2(11)

　　使用霍夫變換檢測橢圓的基本算法［9］為：首先查找圖像中的邊緣點(diǎn),，找到距離滿足給定條件的兩點(diǎn),，這兩點(diǎn)被看成是橢圓主軸上的兩個(gè)端點(diǎn)，然后對圖像邊緣上的每一個(gè)點(diǎn)根據(jù)式(6)將其轉(zhuǎn)化到圖2所對應(yīng)的坐標(biāo)系中,，若得到的點(diǎn)的坐標(biāo)滿足條件(10)和(11),，則由式(2)計(jì)算出橢圓的短半軸的長度，最后根據(jù)短半軸長度將短半軸聚集矩陣中對應(yīng)項(xiàng)的值加1。如果最終聚集矩陣中的某一項(xiàng)的值大于給定的閾值,，則該項(xiàng)對應(yīng)的邊緣像素點(diǎn)在同一橢圓上,。假設(shè)橢圓的主軸上的兩個(gè)端點(diǎn)分別為(x1,y1)和(x2,y2)，則橢圓的中心O(x0,y0),、長半軸a及橢圓長軸與x軸的夾角T如下:

　　獲取橢圓的短半軸的長度,，需要先按照式(6)將邊緣點(diǎn)的坐標(biāo)轉(zhuǎn)化到圖2所示的坐標(biāo)系中，需要4次乘法,，4次加法,，然后求解x2t需要1次乘法，求解y2t需要1次乘法,，接著檢查條件(11)需要1次加法,，最后按照式(2)求解短半軸長度需要1次乘法，1次除法,，1次減法和1次求平方根,。因此求解短半軸的長度總共需要8次乘除法，6次加減法和1次求平方根,。在文獻(xiàn)［9］介紹的方法中,，求解短半軸的長度需要11次乘除法，8次加減法和2次求平方根,。經(jīng)過比較可以看出,，本文提供的方法需要的運(yùn)算量要小一些。

2減少用于計(jì)算短半軸長度的點(diǎn)數(shù)

　　在前面介紹的橢圓檢測算法中,，需要將邊緣像素點(diǎn)轉(zhuǎn)化到圖2所示的坐標(biāo)系后才能判斷該點(diǎn)是否在某一個(gè)橢圓上,，然后計(jì)算該橢圓的短半軸的長度。明顯不在橢圓上的點(diǎn)不必要進(jìn)行轉(zhuǎn)化,，這樣可以減少計(jì)算量,。在橢圓邊界盒子外的點(diǎn)明顯不在橢圓上，不必轉(zhuǎn)化而將其排出,。使用與坐標(biāo)軸平行的邊界盒子,，圖3橢圓邊界示意圖如圖3所示，圖中最大的長方形即為邊界盒子,。設(shè)橢圓邊界盒子的寬為W,， 高為H。邊界盒子的寬和高的計(jì)算式如下：

　　H=2a|cosT|+2bsinT(17)

　　W=2asinT+2b|cosT|(18)

　　上式中,，b為橢圓的短半軸的最大長度,，其最大值為a。橢圓的中心為O(x0,y0),，若點(diǎn)的坐標(biāo)滿足條件

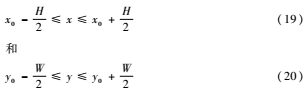
　　則將其轉(zhuǎn)化到圖2所示的坐標(biāo)系后求解短半軸的長度,。

3橢圓檢測的步驟

　　算法的輸入是從圖像中取得的邊緣像素點(diǎn)的列表 L,，輸出是找到的橢圓的中心O(x0,y0)，長半軸a,，短半軸b,，長軸與x軸的夾角T以及橢圓的邊上的點(diǎn)。

　　根據(jù)前面對橢圓檢測算法的描述,，橢圓檢測的步驟如下：

　　(1)在L中尋找距離在給定范圍內(nèi)的兩點(diǎn)A,B,，如果存在這樣的兩點(diǎn)，則跳到第（2)步,，否則結(jié)束,。

　　（2)將A,B作為橢圓長軸的兩個(gè)端點(diǎn),，按照式(12),、(13)、(14),、(15),、(16)計(jì)算出橢圓的中心O(x0,y0)、長半軸a,、橢圓長軸與x軸的夾角T,。

　　（3)按照式(17),、(18)分別計(jì)算出橢圓邊界盒子的高H和寬W,。

　　（4)將短半軸聚集累加器中的每一項(xiàng)清零,。

　?。?)對于L中的每一個(gè)點(diǎn)，如果點(diǎn)的坐標(biāo)滿足式(19),、(20),，則將其坐標(biāo)由式(6)轉(zhuǎn)化到圖2所對應(yīng)的坐標(biāo)系中，然后判斷得到的坐標(biāo)是否滿足式(10)和(11),，如果滿足,，則按照式(2)計(jì)算出短半軸的長度及聚集累加器中的對應(yīng)項(xiàng)加1。

　?。?)在短半軸聚集累加器中查找值大于給定閾值的項(xiàng),，輸出該項(xiàng)對應(yīng)的橢圓的長半軸長度a、短半軸長度b,、中心坐標(biāo)(x0,y0)、長軸與x軸的夾角T以及該橢圓對應(yīng)的邊上的點(diǎn),。將該橢圓邊上的點(diǎn)從L中刪除,。跳到第（1)步。

4合成圖像和真實(shí)圖像測試結(jié)果

　　使用合成的圖像作為測試數(shù)據(jù)，先使用Sobel算子計(jì)算出圖像的梯度,，然后使用簡單閾值算法找到圖像的邊緣像素點(diǎn)列表,。使用從圖像中獲取的邊緣像素點(diǎn)列表，根據(jù)前面的橢圓檢測步驟檢測圖像中的橢圓,。測試使用的圖像以及檢測到的橢圓和橢圓邊緣點(diǎn)如圖4所示,。測試用的圖像大小為640×480。檢測到的圖像中的橢圓的參數(shù)如表1所示,。按照測試圖像中橢圓從左到右,，從上到下，同心橢圓 (圓) 從小到大的順序,，橢圓的數(shù)據(jù)在表中以這個(gè)順序列出,。表中的 “數(shù)據(jù)無效” 表示檢測對象是圓，其長軸與x軸的夾角無意義,；夾角T的單位為弧度,。

　　從檢測結(jié)果來看，測試圖像中的橢圓 (圓) 被全部檢測到,，得到的橢圓 (圓) 的參數(shù)比較準(zhǔn)確,。從圖4中檢測到的橢圓圖像看，在長軸端點(diǎn)附近的點(diǎn)沒有被檢測到,，這是由于當(dāng)邊緣點(diǎn)靠近長軸端點(diǎn)時(shí),，由式(2)求得的橢圓的短半軸的長度誤差大。

　　使用真實(shí)的圖像進(jìn)行測試,。先對測試圖使用高斯低通慮波器除噪聲,，然后使用Sobel算子求圖像的梯度，接著使用簡單閾值算法得到圖像的邊緣,，再進(jìn)行痩邊處理［8,，16］，得到圖像的邊緣像素點(diǎn)列表,，最后根據(jù)前面的橢圓檢測步驟檢測圖像中的橢圓,。測試圖像的大小為 640×480。測試結(jié)果如圖5所示,，從測試結(jié)果看,，圖中的橢圓被全部檢測出。橢圓檢測算法所找到的橢圓 (圓) 的邊緣點(diǎn)在圖中使用實(shí)線標(biāo)示出,。

5結(jié)論

　　本文介紹的橢圓檢測算法使用一維的聚集累加器,，需要的內(nèi)存少，受噪聲的影響小,，算法對橢圓的檢測比較準(zhǔn)確,。橢圓檢測算法需要橢圓長軸上的兩個(gè)端點(diǎn),，如果橢圓長軸上的兩個(gè)端點(diǎn)不存在，則橢圓不會(huì)被檢測到,。算法需要先找橢圓長軸上的兩個(gè)端點(diǎn),，然后令一個(gè)點(diǎn)在以這兩個(gè)端點(diǎn)為長軸的橢圓上，計(jì)算出這個(gè)橢圓的短半軸的長度,，圖像的邊緣點(diǎn)很多,，算法的運(yùn)算量很大。通過Sobel算子求解圖像中的邊緣點(diǎn)方向［8］,，根據(jù)邊緣點(diǎn)的方向?qū)⑦吘夵c(diǎn)分成兩部分,，方向相對的各為一部分，然后分別在這兩部分中查找橢圓的長軸端點(diǎn),，以減少可能的橢圓長軸的端點(diǎn)數(shù)目,。由于圖像中的邊存在大量的直線，如果一個(gè)邊緣點(diǎn)不是可能的橢圓長軸端點(diǎn),，則其附近的點(diǎn)為橢圓的長軸上的端點(diǎn)的可能性比較小,。如果一個(gè)點(diǎn)被作為橢圓的長軸上的點(diǎn)被檢測，則它附近的點(diǎn)可以不再作為長軸的端點(diǎn)進(jìn)行檢測,，利用Sobel算子求解出的邊緣點(diǎn)的方向信息,，將圖像中臨近的邊緣點(diǎn)中方向很相近的點(diǎn)只保留一個(gè)進(jìn)行可能的長軸端點(diǎn)檢測，因?yàn)槿绻吘夵c(diǎn)的方向相同,，則認(rèn)為在同一直線上,，不大可能成為橢圓的邊，這種方法能減少大量的運(yùn)算量,，但是誤差較大,。

　　參考文獻(xiàn)

　　［1］ YIN P Y, CHEN L H. New method for ellipse detection by means for symmetry［J］. Journal of Electronic Imaging, 1994, 3(1): 20-29.

　?。?］ HO C, CHEN L. A fast ellipse/circle detector using geometric symmetry［J］. Pattern Recognition, 1995, 28(1): 117-124.

　?。?］ AGUADO A S, MONTIEL M E, NIXON M S. On using directional information for parameter space decomposition in ellipse detection［J］. Pattern Recognition, 1996, 29(3): 369-381.

　　［4］ LEI Y, WONG C. Ellipse detection based on symmetry［J］. Pattern Recognition, 1999, 20: 41-47.［5］ DAVIES E R. Finding ellipses using the generalized Hough Transform［J］. Pattern Recognition, 1989,9（2）: 87-96.

　?。?］ TSUJI S, MATSUMOTO F. Detection of ellipses by modified Hough Transform［J］. IEEE Transaction On Computers, 1978, 27(8): 777-781.

　?。?］ YIP R K K, TAM P K S, LEUNG D N K. Modification of Hough Transform for circles and ellipses detection using a 2-dimensional array［J］. Pattern Recognition, 1992, 25(9): 10071022.

　　［8］ DAVIES E R. Computer & Machine Vision［M］. 北京：機(jī)械工業(yè)出版社, 2013.

　?。?］ Xie Yonghong, Ji Qiang. A new efficient ellipse detection method［C］. 16th International Conference Pattern Recgnition, Proceedings.  Quebec, Canada, 2002,， IEEE, 2002: 957960.

　　［10］ Ji Qiang, HARALICK R M. A statistically efficient method for ellipse detection［C］. Proceedings of 1999 International Conference on Image Processing USA: IEEE Computer Society Press, 1999:730-734.

　?。?1］ BALLARD D H. Generalizing the Hough transform to detect arbitrary shapes［J］. Pattern Recognition, 1981, 13(2): 111-122.

　?。?2］ HART P E. How the Hough Transform was invented［C］. IEEE Signal Processing, 2009: 1822.

　　［13］ DUDA R O, HART P E. Use of the Hough Transform to detect lines and curves in pictures［J］. Communications of the ACM, 1972, 15(1): 1115.

　?。?4］ HEARN D, BAKER M P. Computer graphics with OpenGL［M］. 北京：電子工業(yè)出版社, 2006.

　?。?5］ LAY D C. Linear algebra and its applications［M］. 北京：電子工業(yè)出版社, 2010.

　?。?6］ GONZALEZ R C, WOODS R E. Digital image processing［M］. 北京：電子工業(yè)出版社, 2007.