李常春1，陳  彬1,，黃銀華2,，盧  欣1， 李  磊1

　?。?.國(guó)網(wǎng)天津市電力公司電力科學(xué)研究院,，天津 300000;2.福建省電力設(shè)計(jì)院， 福建 福州 350003）

　　摘  要： 介紹了新型電力系統(tǒng)仿真軟件InterPSS和三種潮流計(jì)算方法的基本原理,，基于InterPSS軟件建立了IEEE-30節(jié)點(diǎn)系統(tǒng)仿真模型并進(jìn)行三種方法的潮流仿真計(jì)算,，比較了同一收斂精度水平下三種潮流計(jì)算方法的收斂性，并對(duì)高斯-塞得爾法中加速因子的作用機(jī)理進(jìn)行了分析,。最后展望了InterPSS在電力系統(tǒng)仿真中的應(yīng)用前景,。

　　關(guān)鍵詞： InterPSS；潮流計(jì)算,；收斂性,；電力系統(tǒng)仿真,；加速因子

0 引言

　　隨著計(jì)算機(jī)技術(shù)和網(wǎng)絡(luò)技術(shù)在電力系統(tǒng)中的應(yīng)用越來越廣泛，現(xiàn)在已經(jīng)有越來越多的電力系統(tǒng)運(yùn)行控制調(diào)度,、電力系統(tǒng)設(shè)計(jì),、仿真等工作都由計(jì)算機(jī)來完成,。由此產(chǎn)生的眾多電力系統(tǒng)運(yùn)行,、仿真軟件也在電力系統(tǒng)中得到廣泛應(yīng)用，比較常用的有PSASP,、BPA,、EMTP、PSCAD/EMTDC,、NETOMAC等,。但是這些仿真軟件都或多或少地存在不利于維護(hù)、難以擴(kuò)展和不易與其它系統(tǒng)兼容等問題,。InterPSS基于Internet和面向?qū)ο蟮募夹g(shù),，使用靈活，擴(kuò)展方便,，有效克服了上述弊端,。本文通過InterPSS軟件建立了IEEE-30電力系統(tǒng)的模型，進(jìn)行了三種潮流計(jì)算的仿真和比較,，在不同加速因子下進(jìn)行了高斯-塞得爾迭代方法潮流仿真計(jì)算,，分析了加速因子對(duì)潮流計(jì)算收斂性的影響。

1 典型潮流計(jì)算方法概述

　　利用電子計(jì)算機(jī)進(jìn)行電力系統(tǒng)潮流計(jì)算從上個(gè)世紀(jì)50年代中期就已開始,。在過去的幾十年里,，采用了各種不同的計(jì)算方法。各種計(jì)算方法都必須綜合考慮以下因素[1]：（1）計(jì)算方法的可靠性或收斂性,；（2）對(duì)計(jì)算機(jī)內(nèi)存的要求,；（3）計(jì)算速度；（4）計(jì)算的方便性和靈活性,。

　　電力系統(tǒng)潮流計(jì)算在數(shù)學(xué)上表現(xiàn)為一組多元非線性方程式的求解問題,，其解法都離不開迭代。即在假設(shè)某一組狀態(tài)（母線電壓）的情況下求殘差（母線注入功率）,，根據(jù)殘差再修正狀態(tài),，直至殘差或修正值達(dá)到要求為止。高斯-塞得爾法就是一種最基本的非線性方程的迭代算法,。

　　1.1 高斯-塞得爾法（GS法）

　　利用高斯-塞得爾法可直接迭代解節(jié)點(diǎn)電壓方程,將節(jié)點(diǎn)電壓方程展開,，移項(xiàng)可得

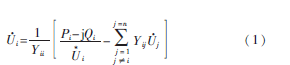
　　將上式進(jìn)一步展開即得高斯-塞得爾法的迭代公式[2]。

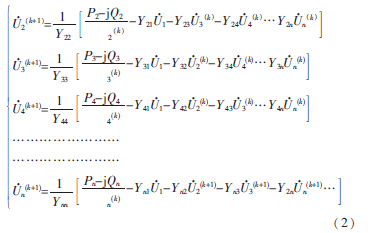
　　式中Pi-jQi——給定的各節(jié)點(diǎn)注入功率的共軛值,，i=1,、2、……、n,；

　?。铡? ——給定的平衡節(jié)點(diǎn)電壓；

　　k——迭代次數(shù),。

　　當(dāng)某一次迭代解得的Ｕ·i（k+1）與（i=2,、3、4,、……n）前一次迭代解得的Ｕ·i（k）（i=2,、3、4,、……n）相差小于事先給定的允許誤差,，即|Ｕ·i（k+1）-Ｕ·i（k）| （i=2、3,、4,、……n）時(shí)，認(rèn)為迭代已收斂,。

　　以上假設(shè)沒有PV節(jié)點(diǎn),，在有PV節(jié)點(diǎn)的情況下，由于這些節(jié)點(diǎn)的電壓要求,，其無功受限制,，應(yīng)對(duì)上述公式予以修正，在此不再贅述,。

　　1.2 牛頓-拉夫遜法（NR法）

　　牛頓-拉夫遜法是解非線性方程式的有效方法,。這個(gè)方法把非線性方程式的求解過程變成反復(fù)對(duì)相應(yīng)的線性方程的求解過程，通常稱為逐次線性化過程,，這是牛頓-拉夫遜法的核心,。由于電力系統(tǒng)的龐大和復(fù)雜性，在潮流計(jì)算中,，往往要進(jìn)行高階的非線性方程組的求解,。概括地講，潮流計(jì)算是由系統(tǒng)各節(jié)點(diǎn)給定的復(fù)功率求解各節(jié)點(diǎn)電壓向量的問題,。在極坐標(biāo)情況下節(jié)點(diǎn)功率方程式如下[2],。

　　式中, θij=θi-θj為i、j兩節(jié)點(diǎn)電壓的相角差,，Pi,、Qi分別為節(jié)點(diǎn)的有功和無功功率，Vi,、Vj為節(jié)點(diǎn)電壓,，Gij,、Bij為節(jié)點(diǎn)i、j之間電導(dǎo)和電納,。

　　極坐標(biāo)下的修正方程如下式：

　　通過反復(fù)地迭代修正方程,，直至功率不平衡量滿足以下條件：

　　||ΔP（t）, ΔQ（t）||<ε（5）

　　判定迭代收斂。其中||ΔP（t）, ΔQ（t）||是向量ΔP（t）, ΔQ（t）中最大的分量的絕對(duì)值,。

　　牛頓-拉夫遜法由于它的收斂性較好且由于修正方程式的稀疏性,，節(jié)約了大量的計(jì)算機(jī)內(nèi)存并減少了運(yùn)算量，從而有較高的計(jì)算速度,。所以在上個(gè)世紀(jì)60年代后期成為了應(yīng)用最廣泛的解決系統(tǒng)潮流的方法,。目前仍作為一種主要的潮流計(jì)算方法大量使用,。相比高斯-塞得爾法,，其在收斂性和運(yùn)算速度上都有很大改進(jìn)[3]。

　　1.3  P-Q分解法（PQ法）

　　P-Q分解法是極坐標(biāo)下的牛頓-拉夫遜法的基礎(chǔ)上通過改進(jìn)和簡(jiǎn)化而來的,。它的基本思想是：把節(jié)點(diǎn)功率表示為電壓向量的極坐標(biāo)方程式,，抓住主要矛盾，以有功功率誤差作為修正電壓向量角度的依據(jù),，以無功功率誤差作為修正電壓幅值的依據(jù),，把有功功率和無功功率迭代分開進(jìn)行。從而達(dá)到快速解耦潮流計(jì)算的目的[2],。

　　在牛頓-拉夫遜法的修正方程基礎(chǔ)上,，考慮大型電網(wǎng)的兩個(gè)特性：（1）大型電網(wǎng)中，各元件的電抗一般遠(yuǎn)遠(yuǎn)大于電阻,。從而各節(jié)點(diǎn)的電壓相位的改變主要影響各元件中的有功功率潮流,，也就是影響各節(jié)點(diǎn)的注入有功功率；各節(jié)點(diǎn)電壓的大小改變主要影響各元件中的無功功率潮流也就是影響各節(jié)點(diǎn)的注入無功功率,。（2）一般線路兩端的相角差不會(huì)很大（通常不超過）,。從而得到簡(jiǎn)化的功率誤差方程式：

　　P-Q法相對(duì)于牛頓-拉夫遜法，無論是在計(jì)算速度和內(nèi)存方面都有很大改善,。由于迭代時(shí)的雅可比矩陣就是導(dǎo)納矩陣的虛部,，因此在迭代過程中不必像牛頓-拉夫遜法那樣進(jìn)行形成雅可比矩陣的計(jì)算，這樣不僅減少了運(yùn)算量,，而且也大大簡(jiǎn)化了程序,。另外，由于系數(shù)矩陣在迭代過程中維持不變,，顯著提高了迭代速度,。由于P-Q法大大提高了潮流計(jì)算的速度，不僅可以用于離線計(jì)算,，還可以用于在線電力系統(tǒng)安全監(jiān)視,，因此P-Q法獲得了非常廣泛的應(yīng)用,，是目前最流行的潮流計(jì)算方法。

2  InterPSS軟件簡(jiǎn)介

　　InterPSS是建立在互聯(lián)網(wǎng)（Internet）技術(shù)基礎(chǔ)之上開發(fā)的新一代電力系統(tǒng)仿真軟件系統(tǒng),。它基于一個(gè)面向?qū)ο螅∣bject-Oriented）電力系統(tǒng)仿真框架（Framework）,，采用靈活的、可擴(kuò)展的軟件結(jié)構(gòu),。在該結(jié)構(gòu)中,，軟件模塊可以相互交換和靈活嵌入。InterPSS 包括潮流計(jì)算,、短路計(jì)算,、繼電保護(hù)協(xié)調(diào)、諧波分析,、暫態(tài)穩(wěn)定性計(jì)算,、動(dòng)態(tài)穩(wěn)定性小擾動(dòng)計(jì)算、可靠性分析及許多典型電力系統(tǒng)設(shè)計(jì),、分析和仿真模塊,。作為一個(gè)開放式的電力系統(tǒng)仿真綜合集成平臺(tái),它使任何按照InterPSS仿真框架接口規(guī)范開發(fā)的電力系統(tǒng)仿真算法、用戶界面和輸入輸出模塊, 都能方便地嵌入InterPSS[4-6],。

3 潮流計(jì)算實(shí)例仿真與分析

　　3.1 不同潮流計(jì)算方法收斂性比較與分析

　　本文利用InterPSS軟件的潮流計(jì)算仿真功能,，在同一收斂精度下，對(duì)IEEE-30節(jié)點(diǎn)系統(tǒng)進(jìn)行仿真,。IEEE-30系統(tǒng)如圖1所示,。

　　在收斂精度為0.000 1 p.u.，即允許的最大功率不平衡量為10 kVA時(shí)（系統(tǒng)的功率基準(zhǔn)為100 MVA）,，實(shí)驗(yàn)測(cè)得各種算法的最大迭代次數(shù)如表1所示,。

　　由表1可知，在相同的條件下,，對(duì)IEEE-30系統(tǒng)進(jìn)行潮流計(jì)算時(shí),，NR法所需的迭代次數(shù)最少，PQ法次之,，GS法所需的迭代次數(shù)最多,。表中數(shù)據(jù)說明：

　　（1）GS法相對(duì)于其它兩種算法,，在收斂性方面確實(shí)難以匹敵,。這是因?yàn)榕ｎD-拉夫遜法采用梯度法求解，因而具有二階的收斂速度,；而P-Q分解法在迭代過程中由于雅可比矩陣的不變性,，而大大提高了迭代的速度從而加快潮流收斂的速度。

　?。?）NR法所需的迭代次數(shù)比PQ法少,。PQ法所采取的一系列簡(jiǎn)化假定只影響了修正方程式的結(jié)構(gòu),，也就是說只影響了迭代過程，但并不影響最終結(jié)果,。因?yàn)镻Q法和NR法都采用了相同的數(shù)學(xué)模型,，最后計(jì)算功率誤差和判斷收斂條件都嚴(yán)格按照精確公式進(jìn)行，所以PQ法和NR法一樣可以達(dá)到很高的精度,。由于迭代過程的改變,，PQ法的收斂特性也就相應(yīng)改變。在數(shù)學(xué)上,，像PQ法那樣依一個(gè)不變的系數(shù)矩陣進(jìn)行非線性方程組的求解迭代,，稱為“等斜率法”，其迭代過程具有幾何級(jí)數(shù)收斂特性,，在對(duì)數(shù)坐標(biāo)上表現(xiàn)為一條直線,。而NR法則是按照平方收斂的，在對(duì)數(shù)坐標(biāo)上表現(xiàn)為一拋物線,。

　　在迭代開始時(shí),，NR法會(huì)收斂較慢,，但是隨后它的收斂速度非常之快,，而PQ法幾乎是按同一速度收斂的。我們選擇的收斂精度是0.0001 p.u.,，在這個(gè)精度下PQ法的迭代次數(shù)要比NR法多,。另外，PQ法的收斂性還受實(shí)際電壓等級(jí)和參數(shù)的影響,。因?yàn)镻Q法是建立在cos θij≈1,、Gijsinθij<<Bij和Qi<<Bii的假設(shè)條件上的。如果系統(tǒng)參數(shù)不符合這兩個(gè)條件時(shí),，就會(huì)影響它的收斂性,。在高壓電網(wǎng)中一般都能滿足這兩個(gè)條件。本文采用的IEEE-30電網(wǎng)也只是中高壓電網(wǎng),，所以以上假設(shè)條件并不能很好地符合,，這在一定程度上影響了PQ法的收斂性，使迭代次數(shù)有所增加,。

　　3.2  GS法加速因子的影響與分析

　　為進(jìn)一步驗(yàn)證InterPSS在潮流仿真中的正確運(yùn)用,，以下對(duì)GS法在不同的加速因子下的潮流計(jì)算結(jié)果進(jìn)行比較與分析。在不同的加速因子情況下,，GS法對(duì)IEEE-30系統(tǒng)進(jìn)行潮流計(jì)算收斂時(shí)的相應(yīng)迭代次數(shù)如表2所示,。

　　由表2可知，加速因子的使用有利于加快迭代收斂的速度,。并且加速因子的選擇并不是越大越好或是越小越好,。相對(duì)于沒有采用加速因子的情況而言,，采用加速因子可以很明顯的改善迭代計(jì)算的收斂性，這可在數(shù)學(xué)上給出證明,。給出迭代計(jì)算的收斂定理如下[7]：

　　定理　對(duì)于方程f（x）=0, 其迭代形式為

　　x=g（x）（7）

　　若迭代函數(shù)滿足g（x）條件：

　?。╥）在區(qū)間[a,b]上g′（x）存在,且|g′（x）|≤L（其中L為小于1的正常數(shù)）；

　?。╥i）對(duì)任意x∈[a,b],，都有g(shù)（x）∈[a,b]，則：

　?。?） 對(duì)任取初始值x0∈[a,b], 迭代公式xk+1=g（xk）產(chǎn)生的迭代序列{xk}都收斂于方程x=g（x）在[a,b]上的唯一實(shí)根x*,；

　　結(jié)論（1）表明，只要選擇的迭代函數(shù)g（x）在區(qū)間[a,b]滿足條件（i）,（ii）,，那么方程在該區(qū)間上存在唯一的實(shí)根,，而且當(dāng)x0∈[a,b]時(shí)，迭代公式xk+1=g（xk）必收斂,。結(jié)論（2）表明,，要使|x*-xk|≤ε，只要|xk+1-xk|≤ε,，因此可用前后兩次近似根的接近程度,，即用|xk+1-xk|的大小來判斷xk+1是否滿足精度要求。結(jié)論（3）表明常數(shù)L越小,，迭代收斂的速度越快,。

　　應(yīng)用到GS法中，設(shè)潮流的基本方程為f（v）=0,，其第k次迭代的近似根為vk,，則按（7）式有vk+1=g（vk）。將vk+1作為過渡值并記為k+1=g（vk）,，利用vk和k+1的某種線性組合作為新的近似根vk+1,，如vk+1=αk+1+（1-α）vk，其中α的為待定系數(shù),，α的確定方法如下,。

　　設(shè)v*為方程f（v）=0的一個(gè)實(shí)根, 則v*=g（x*），k+1=g（vk）,，兩式相減得

　　v*-k+1=g（v*）-g（vk）

　　由微分中值定理有

　　v*-k+1=g′（ξ）（v*-vk）,ξ∈（v*-vk）,。

　　假設(shè)g′（v）在求根區(qū)間內(nèi)變化不大，則可取某定值m來近似代替,。由于v=g（v）收斂,，因此有|g′（v）|<1，即|m|≈

　　|g′（v）|≤L<1,，則由上式可得v*≈m（v*-vk）+k+1從而

　　由此可得待定系數(shù)α為,，由于|m|<1,，當(dāng)m<0時(shí)，vk+1將在k+1和vk的之間,，稱為內(nèi)插法,；當(dāng)m>0時(shí)，vk+1在k+1和vk的延長(zhǎng)線上,，即所謂的“外插法”,。以下證明采用這種線性組合的方法后可以加速收斂。

　　將（8）式的迭代函數(shù)記為Ψ(v),，則

　　由收斂定理知|g′（v）|≤L<1時(shí)序列{vk}收斂,，且L越小收斂越快，則如果Ψ(v)和g(v)滿足|Ψ′(v)|<|g′(v)|,，就說明式(9）比式(8）式收斂得快,。

　　對(duì)Ψ(v)函數(shù)求導(dǎo)，可得

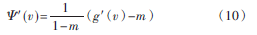
　　由于式(8）假設(shè)g′（v）在求根區(qū)間內(nèi)變化不大且用m來近似代替,，因此g′（v）-m≈0,，即Ψ′(v)很小，接近于0,。所以有|Ψ′(v)|<|g′（v）|,，因此式(8）比式(7）式收斂得快，從而證明了加速因子的確可以加快收斂的速度,。

4 結(jié)語

　　本文基于InterPSS的潮流仿真功能,，通過對(duì)IEEE-30系統(tǒng)進(jìn)行了完整的潮流計(jì)算，得出了在相同的精度和最大迭代次數(shù)情況下各自的迭代次數(shù),。比較了三種潮流計(jì)算方法的收斂性，結(jié)果顯示高斯-塞得爾法的計(jì)算速度和收斂性都遜色于牛頓-拉夫遜法和P-Q分解法,，并論證了這種現(xiàn)象的原因,。此外還從數(shù)學(xué)上證明了高斯-塞得爾法中加速因子的加速收斂作用。

　　本文僅應(yīng)用了InterPSS潮流計(jì)算模塊,，由于該仿真軟件高度開放,，用戶可根據(jù)需求自行編譯計(jì)算模塊，為電力工作者提供了一個(gè)良好的交流和學(xué)習(xí)的平臺(tái),，也必將在未來電力系統(tǒng)仿真計(jì)算中得到更為廣泛和深入的應(yīng)用,。

參考文獻(xiàn)

　　[1]王守相，劉玉田.電力系統(tǒng)潮流計(jì)算研究現(xiàn)狀[J].山東電力技術(shù),1996 (5）:8-12.

　　[2]陳珩.電力系統(tǒng)穩(wěn)態(tài)分析[M].北京:水利水電出版社,1985.

　　[3]李敏,陳金富,段獻(xiàn)忠,等.潮流計(jì)算收斂性問題研究綜述[J].繼電器,2006,34(4）:74-79.

　　[4]ZHOU M, Zhou Shizhao. Open-source and Power System Simulation[EB/OL]. www.interpss.org.1-5.

　　[5]ZHOU E Z. Object-oriented Programming, C++ and Power System Simulation.

　　[6]黃秋華,，張堯,，ZHOU Michael.開放式電力系統(tǒng)仿真軟件InterPSS及其擴(kuò)展[J]. 電力自動(dòng)化設(shè)備，2012,32（10）:138-141,145.

　　[7]邸書靈,劉展威,劉玉宏.關(guān)于非線性方程加速迭代的注記[J].工科數(shù)學(xué),2002,18(5）:82-86.