黃雄波

　?。ǚ鹕铰殬I(yè)技術(shù)學(xué)院 電子信息系,，廣東 佛山 528137）

　　摘要：由于自相關(guān)函數(shù)刻畫(huà)了時(shí)序數(shù)據(jù)在不同時(shí)刻取值的線性相關(guān)程度，故其在時(shí)序數(shù)據(jù)的統(tǒng)計(jì)分析中得到了廣泛的應(yīng)用,。討論了基于FFT變換的自相關(guān)函數(shù)計(jì)算原理,，結(jié)合非平穩(wěn)時(shí)序數(shù)據(jù)的辨識(shí)需求，基于自相關(guān)函數(shù)理論對(duì)趨勢(shì)和周期成份的分離次序以及殘留序列的隨機(jī)類型識(shí)別等問(wèn)題進(jìn)行了深入分析,，進(jìn)一步提出了一種改進(jìn)的非平穩(wěn)時(shí)序數(shù)據(jù)的辨識(shí)算法,。實(shí)驗(yàn)驗(yàn)證了改進(jìn)算法的合理性和有效性。

　　關(guān)鍵詞： 自相關(guān)函數(shù),； FFT變換,；非平穩(wěn)時(shí)序數(shù)據(jù)；系統(tǒng)辨識(shí)

0引言

　　在工程,、經(jīng)濟(jì),、自然和社會(huì)科學(xué)等很多領(lǐng)域中，被考查對(duì)象在其歷史的演變過(guò)程中,，其相關(guān)的物理量常常以一系列隨時(shí)間而變化的數(shù)據(jù)序列而被人們記載,，這種序列通稱為時(shí)間序列或時(shí)序數(shù)據(jù) ［13］。事實(shí)上,，由于受到諸多偶然因素的影響,，時(shí)序數(shù)據(jù)很難用一個(gè)精確的數(shù)學(xué)表達(dá)式來(lái)描述，但由于它們大都具有統(tǒng)計(jì)規(guī)律的特性,，因此,，可以通過(guò)對(duì)時(shí)序數(shù)據(jù)的辨識(shí)和建模，進(jìn)而達(dá)到認(rèn)識(shí)事物,、掌握其內(nèi)在變化規(guī)律的目的［46］,。

　　一般地說(shuō)，事物在演變過(guò)程中往往具有某種趨勢(shì)或周期規(guī)律的特性,，故在現(xiàn)實(shí)中所獲得的時(shí)序數(shù)據(jù)也就具有非平穩(wěn)的特點(diǎn),，即序列的均值(一階矩)為非常數(shù)且自相關(guān)函數(shù)(二階矩)與起始時(shí)間有關(guān)［78］。由于非平穩(wěn)時(shí)序數(shù)據(jù)具有時(shí)變的統(tǒng)計(jì)結(jié)構(gòu),，故其辨識(shí)和建模的過(guò)程比平穩(wěn)時(shí)序數(shù)據(jù)要復(fù)雜得多,，目前比較有效的做法是［913］：首先從原始序列中分離出趨勢(shì)和周期成份并分別對(duì)它們進(jìn)行辨識(shí),，然后對(duì)殘留的平穩(wěn)隨機(jī)序列建立相應(yīng)的AR、MA或ARMA模型,。本文基于自相關(guān)函數(shù)的理論,，對(duì)諸如趨勢(shì)和周期成份的分離次序以及殘留序列的隨機(jī)類型識(shí)別等問(wèn)題進(jìn)行了分析，在此基礎(chǔ)上,，提出一種改進(jìn)的非平穩(wěn)時(shí)序數(shù)據(jù)的辨識(shí)算法,，實(shí)驗(yàn)證明改進(jìn)算法是有效的。

1問(wèn)題描述

　　1.1時(shí)序數(shù)據(jù)的自相關(guān)函數(shù)

　　設(shè)樣本長(zhǎng)度為n的非平穩(wěn)時(shí)序數(shù)據(jù){y(t),t=0,1,…,n－1}在相鄰p時(shí)刻的數(shù)據(jù)取值分別為yt和yt+p,，則yt的p階樣本自相關(guān)函數(shù)的估算值r^(p)可用式(1)進(jìn)行計(jì)算：

　　自相關(guān)函數(shù)是時(shí)序數(shù)據(jù)的二階統(tǒng)計(jì)特性,，它表征了序列數(shù)據(jù)項(xiàng)之間的依賴程度及趨勢(shì)的變化情況，據(jù)此,，可以利用自相關(guān)函數(shù)的上述性質(zhì)來(lái)識(shí)別序列的趨勢(shì)和周期成份的顯著性及它們之間的關(guān)聯(lián)信息等,。

　　1.2基于FFT變換的自相關(guān)函數(shù)計(jì)算

　　利用式(1)計(jì)算r^(p)時(shí)，若序列的樣本長(zhǎng)度n比較大,，則所需要的運(yùn)算量也隨之增加,，為了提高運(yùn)算速度，可以利用快速傅里葉變換(Fast Fourier Transformation,，F(xiàn)FT)算法來(lái)實(shí)現(xiàn)對(duì)r^(p)的快速運(yùn)算［14］,。

　　對(duì)r^(p)施行Fourier變換，由式(1)有：

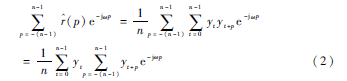
　　為了能用離散傅里葉變換(Discrete Fourier Transform,，DFT)來(lái)計(jì)算式(2)的線性卷積運(yùn)算,，故需要對(duì)時(shí)序數(shù)據(jù)y(t)補(bǔ)充n位零數(shù)值，得y′(t),，即：

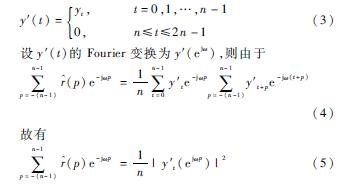
　　綜合式(2)~式(5)可知，基于FFT變換的自相關(guān)函數(shù)的計(jì)算流程為：(1)對(duì)y(t)補(bǔ)充n位零數(shù)值,，得y′(t),；(2) 對(duì)y′(t)做DFT變換，得到y(tǒng)′(m),；(3) 對(duì)1n|y′(m)|2做逆DFT變換,，得到r^′(p)；(4)對(duì)r^′(p)中0~n的點(diǎn)進(jìn)行整體右移n位,，得到r^(p),。

2非平穩(wěn)時(shí)序數(shù)據(jù)的辨識(shí)改進(jìn)

　　2.1自相關(guān)函數(shù)在非平穩(wěn)時(shí)序數(shù)據(jù)的辨識(shí)應(yīng)用

　　非平穩(wěn)時(shí)序數(shù)據(jù)y(t)的辨識(shí)模型如式(6)所示:

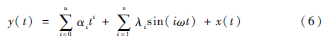
　　其中，∑ui=0αiti是趨勢(shì)成份,，由一個(gè)u階的多項(xiàng)式進(jìn)行辨識(shí),，αi為多項(xiàng)式的各階次的辨識(shí)參數(shù)；∑vi=1λisin(iωt)是周期成份,，ω為基波角頻率,，λi為各諧波的幅值,；x(t)為殘留的平穩(wěn)隨機(jī)序列。

　　2.1.1趨勢(shì)和周期成份的分離

　　對(duì)于既有趨勢(shì)又有周期影響的非平穩(wěn)時(shí)序數(shù)據(jù)而言,，當(dāng)趨勢(shì)成份很強(qiáng)時(shí),，則其趨勢(shì)特點(diǎn)表現(xiàn)突出，甚至?xí)阎芷谔攸c(diǎn)淹沒(méi)掉,；而當(dāng)周期成份很強(qiáng),，其趨勢(shì)特點(diǎn)也有可能顯現(xiàn)不出來(lái)。 據(jù)此,，有必要在現(xiàn)有的非平穩(wěn)時(shí)序數(shù)據(jù)辨識(shí)算法的基礎(chǔ)上,，根據(jù)趨勢(shì)和周期成份在序列中的輕重地位進(jìn)行依次分離和辨識(shí)。

　　對(duì)于趨勢(shì)成份明顯的時(shí)序數(shù)據(jù),，由于緊鄰的數(shù)據(jù)項(xiàng)具有相同的取值方向,，故其自相關(guān)函數(shù)的前3~4階通常會(huì)出現(xiàn)正數(shù)且具有大于2n的特點(diǎn)；而當(dāng)序列存在周期長(zhǎng)度為L(zhǎng)的數(shù)據(jù)成份時(shí),，則由于各個(gè)周期內(nèi)相關(guān)位置的數(shù)據(jù)具有同時(shí)為大或同時(shí)為小的特點(diǎn),，故其L,2L,…,int(nL)L(int()為取整函數(shù))等各階次的自相關(guān)函數(shù)均為正值。依照上述規(guī)則,，可以通過(guò)計(jì)算各階次的自相關(guān)函數(shù)來(lái)判別待辨識(shí)的非平穩(wěn)時(shí)序數(shù)據(jù)是否存在著趨勢(shì)和周期成份,，當(dāng)僅發(fā)現(xiàn)趨勢(shì)時(shí)，則首先分離趨勢(shì)成份,，然后再對(duì)殘留序列進(jìn)行周期識(shí)別,；反之，當(dāng)僅發(fā)現(xiàn)周期時(shí),，則首先分離周期成份,，然后再對(duì)殘留序列進(jìn)行趨勢(shì)識(shí)別；而當(dāng)趨勢(shì)和周期同時(shí)顯著時(shí),，則應(yīng)從原始序列中同時(shí)分離這兩種數(shù)據(jù)成份,。

　　以趨勢(shì)和周期成份同時(shí)顯著為例，其基于最小二乘法的分離過(guò)程如下：

　　為滿足arg mine=∑nt=0|y(t)－f(t)|2,，依最小二乘法有：

　　

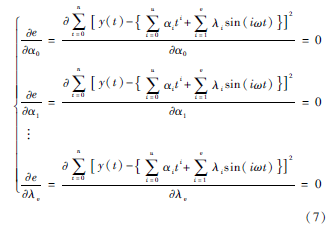
　　求解式(7)的線性方程組［15］,，便可得到趨勢(shì)和周期成份同時(shí)顯著時(shí)的辨識(shí)參數(shù)向量［α0,α1,…,αu,λ1,λ2,…,λv］T。

　　2.1.2殘留序列的平穩(wěn)性判別及辨識(shí)

　　通常,，非平穩(wěn)時(shí)序數(shù)據(jù)y(t)在去掉趨勢(shì)和周期成份的影響后,，其殘留序列x(t)可能是一個(gè)分段局部平穩(wěn)、整體平穩(wěn)或完全隨機(jī)型的序列,，故在殘留序列x(t)的辨識(shí)之前還應(yīng)進(jìn)行隨機(jī)類型的識(shí)別,。完全隨機(jī)型序列其各階次的自相關(guān)函數(shù)具有零值的特點(diǎn)；而分段局部平穩(wěn)或整體平穩(wěn)的隨機(jī)型序列在平穩(wěn)范圍內(nèi)其數(shù)據(jù)項(xiàng)之間是允許存在自相關(guān)的,，但數(shù)據(jù)項(xiàng)xt和xt+p的相關(guān)性會(huì)隨著間隔項(xiàng)p的增大而減少,。在工程應(yīng)用中,，若某序列的各階次的自相關(guān)函數(shù)滿足式(8)，則可把該序列視為平穩(wěn)時(shí)序數(shù)據(jù)［16］,。

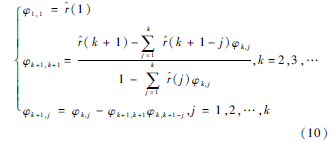
　　式(8)中,，符號(hào)“&&”為邏輯與運(yùn)算，“int( )”為取整函數(shù),，該邏輯表達(dá)式描述了序列的自相關(guān)函數(shù)的絕對(duì)值在1~2階次時(shí)均大于2n,，但其后便衰減至－2n,2n區(qū)間內(nèi)。

　　由于完全隨機(jī)型序列不包含任何形式的模型,，故無(wú)需對(duì)它進(jìn)行任何的處理,；而平穩(wěn)隨機(jī)序列則可以采用式(9)的AR模型進(jìn)行建模：

　　x(t)=φ1xt－1+φ2xt－2+…+φkxt－k+un(9)

　　式(9)中，［φ1,φ2,…,φk］T為自回歸參數(shù)向量,，un是均值為零,、方差為σ2的正態(tài)分布白噪聲。自回歸參數(shù)向量［φ1,φ2,…,φk］T可用式(10)的DurbinLevinson遞推公式求得,，而遞推的具體計(jì)算流程則如圖1所示,。

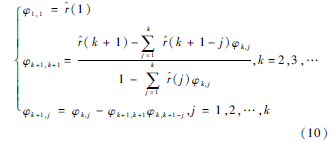
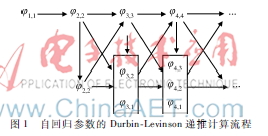
　　對(duì)于分段局部平穩(wěn)的殘留序列而言，在辨識(shí)之前還應(yīng)完成各段平穩(wěn)子序列的劃分,，即需要確定平穩(wěn)子序列的段數(shù)及各段之間的分割點(diǎn),。根據(jù)平穩(wěn)時(shí)序數(shù)據(jù)的自相關(guān)函數(shù)特征，可得到如下平穩(wěn)子序列的分割方法：以1個(gè)數(shù)據(jù)項(xiàng)為步長(zhǎng)自左至右地搜索分割點(diǎn),，若新增數(shù)據(jù)項(xiàng)后的子序列其自相關(guān)函數(shù)仍滿足式(8)中的邏輯表達(dá)式,，則合并該新增數(shù)據(jù)項(xiàng)并繼續(xù)向右搜索；否則以該新增數(shù)據(jù)項(xiàng)為分割點(diǎn),，新建另一平穩(wěn)子序列并繼續(xù)向右搜索,；重復(fù)上述過(guò)程直至遍歷整個(gè)殘留序列為止。完成平穩(wěn)子序列的劃分后,，便可根據(jù)式(10)中的遞推公式求得它們各自的辨識(shí)參數(shù)向量,。

　　2.2非平穩(wěn)時(shí)序數(shù)據(jù)的辨識(shí)改進(jìn)算法

　　綜上所述，可設(shè)計(jì)如下的非平穩(wěn)時(shí)序數(shù)據(jù)的辨識(shí)改進(jìn)算法,。

　　算法：基于自相關(guān)函數(shù)的非平穩(wěn)時(shí)序數(shù)據(jù)的辨識(shí)算法。

　　輸入：樣本長(zhǎng)度為n的非平穩(wěn)時(shí)間數(shù)據(jù)y(t),。

　　輸出：趨勢(shì)成份的辨識(shí)參數(shù)向量［α0,α1,…,αu］T,，周期成份的辨識(shí)參數(shù)向量［λ1,λ2,…,λv］T，隨機(jī)成份的辨識(shí)參數(shù)向量［φ1,φ2,…,φk］T,。

　　步驟1設(shè)計(jì)相關(guān)的公用函數(shù)模塊,。

　　模塊1依照上述的式(2)～式(5)編寫(xiě)序列的FFT自相關(guān)函數(shù)計(jì)算模塊。

　　模塊2編寫(xiě)趨勢(shì)成份顯著的識(shí)別模塊,，具體的識(shí)別流程為：

　　if((r^(1)>(2/sqrt(n)))&&(r^(2)>(2/sqrt(n)))&&(r^(3)>(2/sqrt(n))))

　　{

　　標(biāo)識(shí)趨勢(shì)成份顯著,；

　　}

　　模塊3編寫(xiě)周期成份顯著的標(biāo)識(shí)模塊,，具體的識(shí)別流程為：

　　for(L=2;L<=int(2/n);L++)

　　{//遍歷搜索顯著的周期成份

　　if((r^(L)>0)&&(r^(2*L)>0)&&…&&(r^(int(n/L)*L)>0))

　　{

　　標(biāo)識(shí)周期成份顯著；

　　}

　　}

　　模塊4線性方程組(系數(shù)矩陣A=［aij］∈Rn×n)的GaussSeidel迭代求解模塊,，其迭代求解公式為：

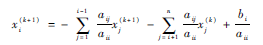
　　步驟2從非平穩(wěn)時(shí)序數(shù)據(jù)中分離趨勢(shì)和周期成份,。

　　(1)調(diào)用公用模塊1計(jì)算y(t)的r^(1)、r^(2),、…,、r^(2n)等各階次的自相關(guān)函數(shù)；

　　(2)調(diào)用公用模塊2和模塊3進(jìn)行趨勢(shì)和周期成份的識(shí)別,；

　　(3)對(duì)(2)的識(shí)別結(jié)果進(jìn)行處理,，分“僅趨勢(shì)成份顯著”、“僅周期成份顯著”,、“趨勢(shì)和周期成份同時(shí)顯著”,、“趨勢(shì)和周期均不顯著”4種情況；

　　case1://限于篇幅,，這里只給出“僅趨勢(shì)成份顯著”的處理流程

　　{

　　(1)基于最小二乘法計(jì)算趨勢(shì)成份顯著時(shí)y(t)所對(duì)應(yīng)的線性方程組的系數(shù)矩陣A,；

　　(2)調(diào)用公用模塊4求得趨勢(shì)成份的辨識(shí)參數(shù)向量［α0,α1,…,αu］T；

　　(3)計(jì)算殘留序列,，x(t)=y(t)－∑ui=0αiti－1,；

　　(4)調(diào)用公用模塊1計(jì)算殘留序列x(t)的r^(1)、r^(2),、…,、r^(2n)等各階次的自相關(guān)函數(shù)；

　　(5)調(diào)用公用模塊3對(duì)殘留序列x(t)進(jìn)行周期成份的識(shí)別,；

　　(6)對(duì)殘留序列x(t)的周期成份識(shí)別結(jié)果進(jìn)行處理：

　　if(殘留序列x(t)的周期成份顯著)

　　{

　?、倩谧钚《朔ㄓ?jì)算周期成份顯著時(shí)x(t)所對(duì)應(yīng)的線性方程組的系數(shù)矩陣A；

　?、谡{(diào)用公用模塊4求得周期成份的辨識(shí)參數(shù)向量［λ1,λ2,…,λv］T,；

　　③更新殘留序列,，x(t)=x(t)－∑vi=1λi(siniωt),；

　　}

　　④轉(zhuǎn)步驟3,；

　　}

　　步驟3對(duì)殘留序列x(t)進(jìn)行辨識(shí),。

　　(1)遍歷殘留序列x(t)，完成各局部平穩(wěn)子序列的劃分,；

　　for(i=0;i<n;i++)

　　{

　　sl=i－d［m］;

　　//計(jì)算當(dāng)前子序列的序列長(zhǎng)度,，d［m］為第m段平穩(wěn)子序列的起點(diǎn)位置

　　if(sl>=min)

　　{

　　if((r^(1)==0)&&(r^(2)==0)&&…&&(r^(int(2/sl))==0))

　　{

　　標(biāo)識(shí)當(dāng)前子序列為完全隨機(jī)型序列；

　　}

　　else

　　{

　　if((abs(r^(1))>(2/sqrt(sl)))&&(abs(r^(2))>(2/sqrt(sl)))&&…&&(abs(r^(3))<(2/sqrt(sl)))&&…&&(abs(r^(int(2/n)))<(2/sqrt(sl))))

　　{

　　標(biāo)識(shí)當(dāng)前的第m段子序列為局部平穩(wěn)子序列,；

　　}

　　else//第i項(xiàng)數(shù)據(jù)為分割點(diǎn)

　　{

　　m++;//局部平穩(wěn)子序列的段數(shù)增1,；

　　d［m］=i;//保存第m段局部平穩(wěn)子序列的分割點(diǎn),；

　　(2)對(duì)平穩(wěn)序列的辨識(shí)參數(shù)向量進(jìn)行估計(jì)：

　　for(i=0;i<m;i++)//m為(1)確定的局部平穩(wěn)子序列的段數(shù)

　　{

　　while(abs(φi_kk)>(2/sqrt(n)))

　　//取顯著性水平α=0.05，若|φi_kk|<2n成立,，則認(rèn)為k階自相關(guān)函數(shù)等于0,；

　　{

　　利用式(10)對(duì)第i段局部平穩(wěn)子序列的辨識(shí)參數(shù)向量［φi_1，φi_2,，…,，φi_k］T進(jìn)行遞推計(jì)算；

　　}

　　步驟4輸出趨勢(shì)成份,、周期成份及隨機(jī)成份的辨識(shí)參數(shù)向量,，算法結(jié)束。

3實(shí)驗(yàn)及結(jié)果分析

　　為了驗(yàn)證上述算法的合理性及有效性,，這里將分別對(duì)趨勢(shì)成份顯著,、周期成份顯著、殘留序列為分段局部平穩(wěn)的非平穩(wěn)時(shí)序數(shù)據(jù)進(jìn)行相關(guān)的辨識(shí)實(shí)驗(yàn),。實(shí)驗(yàn)的硬件環(huán)境為惠普ProDesk 490 G2 MT商用臺(tái)式機(jī)(CPU:i5-45704×3.2 GHz;內(nèi)存:4 GB DDR3 1600),，軟件環(huán)境及開(kāi)發(fā)工具為Windows 8.1+Microsoft Visual C++2010。實(shí)驗(yàn)的主要目的是考察改進(jìn)算法與現(xiàn)有算法之間的辨識(shí)精度及計(jì)算效能,。

　　3.1實(shí)驗(yàn)設(shè)計(jì)

　　不失一般性,，實(shí)驗(yàn)所用的非平穩(wěn)時(shí)序數(shù)據(jù)約定滿足如下假設(shè)：(1)趨勢(shì)成份為二次多項(xiàng)式α0+α1t+α2t2,且α1α0和α1α2成立，即以直線趨勢(shì)成份為主,；(2)周期成份為一次諧波λ1sinωt,；(3)序列的樣本長(zhǎng)度n=200。

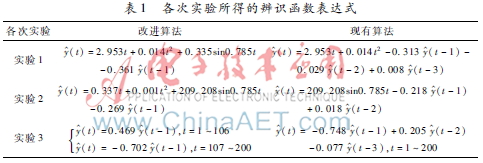
　　分別利用改進(jìn)算法和現(xiàn)有算法進(jìn)行如下實(shí)驗(yàn)：

　　實(shí)驗(yàn)1：趨勢(shì)成份顯著的非平穩(wěn)時(shí)序數(shù)據(jù)的辨識(shí),，所選的數(shù)據(jù)模型如式(11):

　　y(t)=3t+0.011t2+0.3sin0.785t－0.28y(t－1)(11)

　　實(shí)驗(yàn)2：周期成份顯著的非平穩(wěn)時(shí)序數(shù)據(jù)的辨識(shí),，所選的數(shù)據(jù)模型如式（12）：

　　y(t)=0.4t+0.001t2+200sin0.785t－0.28y(t－1)(12)

　　實(shí)驗(yàn)3：殘留序列為分段局部平穩(wěn)的非平穩(wěn)時(shí)序數(shù)據(jù)的辨識(shí)，所選的數(shù)據(jù)模型如式（13）：

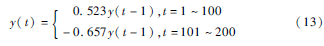
　　3.2實(shí)驗(yàn)結(jié)果與討論

　　為了能全面考察改進(jìn)算法與現(xiàn)有算法的辨識(shí)精度,，這里引入了均方標(biāo)準(zhǔn)誤差(Root Mean Squared Error,，RMSE)和平均絕對(duì)百分誤差(Mean Absolute Percentage Error，MAPE)共兩個(gè)性能評(píng)價(jià)標(biāo)準(zhǔn),，具體定義如式(14)和式(15)所示,。

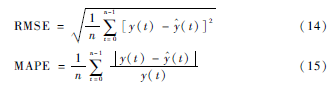
　　式(14)和式(15)中，y(t)為原始序列,，y^(t)為辨識(shí)序列,，n為序列的樣本長(zhǎng)度。

　　實(shí)驗(yàn)1~實(shí)驗(yàn)3的辨識(shí)結(jié)果如表1,、表2及圖2~圖4所示。其中,，表1為辨識(shí)序列的函數(shù)表達(dá)式,，表2為辨識(shí)性能的具體數(shù)值,，而圖2~圖4則是各次實(shí)驗(yàn)的辨識(shí)擬合曲線。

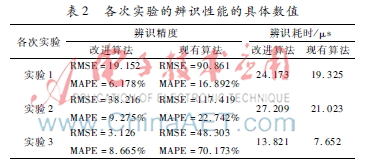
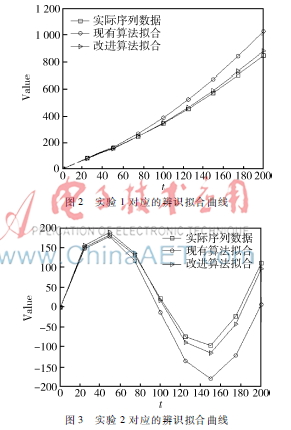
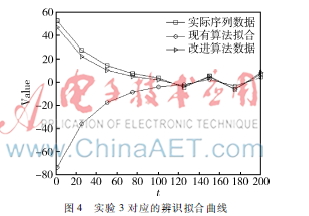
　　從表1的辨識(shí)函數(shù)表達(dá)式易知,，對(duì)于趨勢(shì)或周期成份顯著的非平穩(wěn)時(shí)序數(shù)據(jù)而言,，由于現(xiàn)有算法沒(méi)有按照一定的次序進(jìn)行分離，故不顯著的數(shù)據(jù)成份未能有效地被識(shí)別,，進(jìn)而導(dǎo)致了殘留隨機(jī)序列存在一定的偏差,。在表2中，根據(jù)辨識(shí)性能的具體數(shù)值可發(fā)現(xiàn),，改進(jìn)算法在增加了一定的計(jì)算耗時(shí)后其辨識(shí)精度有了顯著的提高,。從圖4的辨識(shí)擬合曲線則不難發(fā)現(xiàn)，現(xiàn)有算法對(duì)分段局部平穩(wěn)序列的辨識(shí)效果較差,，究其原因是因?yàn)橛昧似椒€(wěn)隨機(jī)模型來(lái)對(duì)整體不平穩(wěn)的序列進(jìn)行辨識(shí),，故不僅存在較大的辨識(shí)誤差而且辨識(shí)序列的模型階數(shù)也出現(xiàn)了增加；而改進(jìn)算法雖然花費(fèi)了相當(dāng)?shù)挠?jì)算耗時(shí),，但能從根本上保證辨識(shí)精度,。綜上所述，本文提出的改進(jìn)算法對(duì)非平穩(wěn)時(shí)序數(shù)據(jù)具有良好的辨識(shí)性能,。

4結(jié)論

　　本文提出了一種非平穩(wěn)時(shí)序數(shù)據(jù)的辨識(shí)改進(jìn)算法,，由于對(duì)趨勢(shì)和周期成份的分離次序以及殘留序列的隨機(jī)類型識(shí)別等細(xì)節(jié)問(wèn)題均作了相應(yīng)的處理，故改進(jìn)算法的辨識(shí)性能有了明顯的提升,。下一步的主要工作是引入自相關(guān)函數(shù)的并行快速變換運(yùn)算,，同時(shí)研究更為有效的平穩(wěn)子序列劃分方法，以便進(jìn)一步提升改進(jìn)算法的計(jì)算效能,。

參考文獻(xiàn)

　?。?］ (德)蓋哈德·克西蓋斯納，(德)約根·沃特斯,，(德)烏沃·哈斯勒.現(xiàn)代時(shí)間序列分析導(dǎo)論［M］.張延群,，劉曉飛，譯.北京: 中國(guó)人民大學(xué)出版社,2015．

　?。?］ (美)漢密爾頓.時(shí)間序列分析［M］．夏曉華,譯.北京:中國(guó)人民大學(xué)出版社,，2015．

　　［3］ 張鵬.飛行數(shù)據(jù)的時(shí)間序列分析方法及其應(yīng)用［M］.北京:國(guó)防工業(yè)出版社,2013．

　?。?］ 趙雪巖,，李衛(wèi)華.系統(tǒng)建模與仿真［M］.北京:國(guó)防工業(yè)出版社,2015．

　　［5］ 蕭德云.系統(tǒng)辨識(shí)理論及應(yīng)用［M］.北京:清華大學(xué)出版社,2014．

　?。?］ 黃介武.線性與廣義線性模型中參數(shù)估計(jì)的一些研究［D］.重慶: 重慶大學(xué),2014．

　?。?］ 楊繼生.非平穩(wěn)綜列數(shù)據(jù)分析：理論與應(yīng)用［M］.北京:中國(guó)社會(huì)科學(xué)出版社,2010．

　　［8］ 王宏禹，邱天爽,，陳哲.非平穩(wěn)隨機(jī)信號(hào)分析與處理(第2版)［M］．北京:國(guó)防工業(yè)出版社,2008．

　?。?］ 黃雄波.時(shí)序數(shù)據(jù)趨勢(shì)項(xiàng)的分段擬合［J］．計(jì)算機(jī)系統(tǒng)應(yīng)用，2015,，24(2):174179．

　?。?0］ 黃雄波.多周期時(shí)序數(shù)據(jù)的傅氏級(jí)數(shù)擬合算法［J］．計(jì)算機(jī)系統(tǒng)應(yīng)用，2015,，24(7):142148．

　?。?1］ 黃雄波.時(shí)序數(shù)據(jù)的周期模式發(fā)現(xiàn)算法的遞推改進(jìn)［J］．計(jì)算機(jī)技術(shù)與發(fā)展，2016,，26(2):4751．

　?。?2］ MAHESWARAN R, KHOSA R.Wavelet volterra coupled models for forecasting of nonlinear and nonstationary time series［J］．Neurocomputing, 2015,  149(Part B, 3):10741084.

　　［13］ SPIRIDONAKOS M D, FASSOIS S D. Nonstationary random vibration modelling and analysis via functional series timedependent ARMA (FSTARMA) modelsA critical survey［J］．Mechanical Systems and Signal Processing, 2014, 47(12):175224.