0 引言

    在無線傳播環(huán)境中,，由于信號可能遇到環(huán)境內(nèi)的障礙物引起的反射、散射以及衍射,，從各個方向傳播到接收端的電磁信號路徑各異,。在過去的研究中常采用大量的測量方法并且得到了一些基于經(jīng)驗(yàn)的統(tǒng)計(jì)模型^[1-3],。然而這些模型只能在信道特性相同的環(huán)境中運(yùn)用，否則產(chǎn)生誤差較大,。射線追蹤法常被應(yīng)用于隨機(jī)信道的建模,，射線傳播遇到散射體時，根據(jù)衍射理論檢測每一條路徑獲取該路徑的信息^[4],，但這種方法建立模型依賴于傳播環(huán)境結(jié)構(gòu)及散射體的具體分布,。因此,，研究人員又提出集合散射模型,，最初提出一個簡單的環(huán)散射模型^[5-6]，之后根據(jù)該模型提出了雙環(huán)散射模型^[7-8],。此外,，有研究人員通過放置一系列點(diǎn)散射體用于分析公路上車輛之間的信道^[9]，且其他研究人員將該方法用于模擬淺水區(qū)聲音傳播信道^[10],。在建立理論模型時為降低復(fù)雜度,，通常假設(shè)散射體服從均勻分布^[6-10]，以往的研究結(jié)果也表明均勻散射體分布模型能較好地?cái)M合多種天線傳播環(huán)境,。上述文獻(xiàn)中均假設(shè)空間對稱分布,，但對于內(nèi)部結(jié)構(gòu)不規(guī)則以及散射體性質(zhì)區(qū)別極大的環(huán)境，都可能使得通信系統(tǒng)呈現(xiàn)出非對稱性,。為降低計(jì)算量并獲得閉合的函數(shù)表達(dá)式,，本文假設(shè)散射體均勻分布，其中接收端(Receiver,，Rx)和發(fā)送端(Transmit,，Tx)任意放置，不僅考慮到直達(dá)(Line Of Sight,，LOS)散射,，并將非直達(dá)(No Line Of Sight，NLOS)散射作為本文的特殊情況,。此外,，本文根據(jù)參考模型提出用于仿真的SOC(Sum Of Cisoids)信道模型，應(yīng)用等面積幾何算法(Generalized Method of Equal Areas,，GMEA)和基本黎曼和方法(Basic Riemann Sum Method,，BRSM)參數(shù)化SOC信道仿真模型，并以多普勒功率譜密度(Power Spectral Density,，PSD)和時間自相關(guān)函數(shù)(Auto Correlation Function,，ACF)為指標(biāo)將二者的性能進(jìn)行比較。

1 禮堂信道散射模型

    如圖1所示,，通常禮堂由最后排觀眾席到主席臺兩側(cè)的寬度逐漸變窄,，外形近似為等腰梯形,，將其豎直投影到二維水平面上，得到如圖2所示的幾何模型,，實(shí)心黑點(diǎn)表示散射體,，A和a分別表示此等腰梯形水平面的下底和上底長，h為等腰梯形的高,。Tx和Rx在梯形內(nèi)的任意位置,，取梯形中心位置（即該梯形中位線的中點(diǎn)處）為坐標(biāo)原點(diǎn)O，Rx沿著x軸勻速運(yùn)動,。假設(shè)NLOS信號只發(fā)生單次反射以及圖2散射區(qū)域內(nèi)所有的散射體均為全向輻射且無反射損耗,。

2 信道參數(shù)及統(tǒng)計(jì)特征

2.1 信道參考模型

    本文通過如下方程對非頻率選擇性衰落信道建立模型：

2.2 AOA概率密度函數(shù)

    本文假設(shè)在坐標(biāo)系用(x，y)表示散射體的位置,，圖2中O的坐標(biāo)為(m,，n)，為了便于分析,，將O移動到Rx處,，新坐標(biāo)系如圖3所示，有x′=x-m,，y′=y-n,。由于Tx的位置對參考模型的統(tǒng)計(jì)特性無任何影響，因此圖3中沒有標(biāo)出Tx的位置,。

    圖3中達(dá)波信號的到達(dá)角度(Angle of Arrival,，AOA)θ可表示：

2.3 多普勒Doppler PSD

3.1 計(jì)算方法

    本文分別采用了GMEA和BRSM計(jì)算SOC仿真模型的參數(shù)c_i、f_i,。根據(jù)GMEA方法,，信道增益c_i為：

3.2 SOC信道統(tǒng)計(jì)特征

4 數(shù)值結(jié)果與分析

    本文假設(shè)梯形上底長a=20 m，下底長A=40 m,，梯形的高h(yuǎn)=40 m,，其余參數(shù)設(shè)置為：f_ρ=60 Hz，σ²=1,，φ_ρ=0°,，f_max=90 Hz，萊斯因子分別取0,、3,、6，SOC仿真模型中設(shè)置樣本函數(shù)的個數(shù)I的值為20,，取m=2,，n=3。由圖4可知,，AOA的PDF在一定范圍內(nèi)單調(diào)遞減或遞增,，且無論信道為寬帶或窄帶,，AOA的PDF都相同。

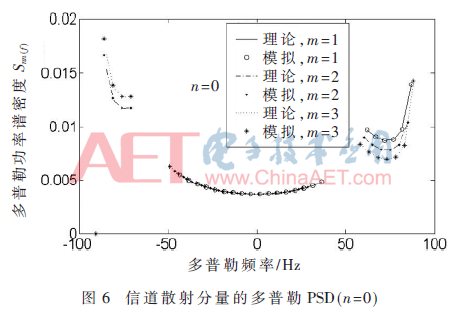
    圖5和圖6表示根據(jù)式(18)仿真出信道散射分量n(t)的多普勒功率密度S_nn(f),，二者分別選定兩個不同的Rx的位置（即分別改變m和n的值）,，由圖可知，當(dāng)多普勒頻率增加時,，其PSD也隨之增加,。圖5表示出當(dāng)m=0時，n(t)的S_nn(f)為頻率相關(guān)且對稱^[14],。而在圖6中令n=0,，情況有所改變。根據(jù)圖5還可看出當(dāng)m=0,，在改變n的值的情況下,，在|f|逼近±f_max時二者值相等。因此,，可以得到結(jié)論：|f|逼近±f_max時，多普勒PSD與n的值無關(guān),，僅僅由m的取值決定^[14],。 

    如圖7所示，仿真模型選取不同的A的值,，并研究其對散射分量S_nn(f)的影響,。由圖可知，增大A的值,，PSD的圖形越來越趨向于完整的字母U的形狀,。在多普勒頻率|f|逼近±f_max時，多普勒PSDS_nn(f)隨著頻率的增加而增加,。

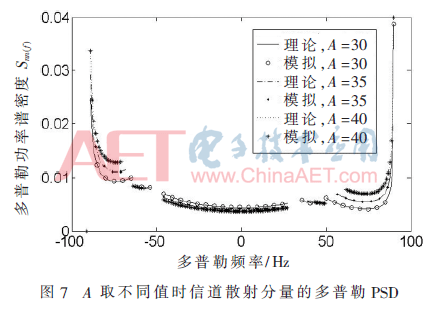
    圖8和圖9分別表示在n(t)的多普勒PSDS_nn(f)對稱的情況下(取m=0,，n=5)，將GMEA和BRSM設(shè)計(jì)的SOC仿真模型與參考模型的時間ACF對比,。由圖可知,，SOC仿真信道模型與參考模型在時間延遲較小時幾乎重合。對比圖8與圖9,，可以看出采用BRSM計(jì)算參數(shù)的SOC仿真信道模型與參考模型相匹配的時間延遲范圍要大于GMEA,。因此，在計(jì)算信道模型時間ACF方面,，BRSM的性能優(yōu)于GMEA,。

    圖10和11分別表示在多普勒PSDS_nn(f)非對稱的情況下(m=2，n=0),，采用GMEA和BRSM的SOC信道仿真模型的時間ACF與參考模型的對比,。由圖可知,，SOC信道仿真模型在一定的時延內(nèi)與參考模型較為吻合。此外,，再次將GMEA與BRSM設(shè)計(jì)的SOC仿真信道對比可知,，BRSM方法在與參考模型相匹配的時間延遲范圍方面要大于前者。因此,，計(jì)算信道模型ACF時,，BRSM的SOC仿真模型的性能更好。

5 結(jié)論

    本文針對典型的禮堂無線傳播環(huán)境中信號傳播的LOS與NLOS情況,，提出基于幾何的散射模型并改進(jìn)得到參考模型,。假設(shè)散射體在散射區(qū)域內(nèi)均勻分布，推導(dǎo)出波達(dá)信號AOA的PDF,、多普勒PSD以及時間ACF的表達(dá)式,，并分析主要參數(shù)對信道模型統(tǒng)計(jì)特性的影響。此外,，本文根據(jù)參考模型設(shè)計(jì)出SOC仿真模型以及BRSM和GMEA兩種方法用于參數(shù)化仿真模型,。結(jié)果表明，BRSM和GMEA都是計(jì)算模型參數(shù)高效準(zhǔn)確的方法,，仿真模型均與對應(yīng)參考模型中的在統(tǒng)計(jì)特性方面較好匹配,，而在時間ACF方面BRSM在一定程度上優(yōu)于GMEA,。文中的結(jié)論不但對于室內(nèi)無線通信性能評估具有重要意義,，且拓寬了高效仿真信道模型的研究。

參考文獻(xiàn)

[1] BAPTISTA A,，HOWE B,，F(xiàn)REIRE J，et al.Scientific exploration in the era of ocean observatories[J].IEEE Computing in Science Engineering,，2008,，10(3)：53-58.

[2] RASHID M T，ALI A A,，ALI R S,，et al.Wireless underwater mobile robot system based on ZigBee[M].New York：ICFCN，2012.

[3] DALBRO M.Wireless sensor networks for off-shore oil and gas installations[M].London：SENSORCOMM,，2008.

[4] SHIN D,，NA S Y，KIM J,，et al.Fish robots for water pollution monitoring using ubiquitous sensor networks with sonar localization[M].New York：ICCIT,，2007.

[5] CHITRE M.A high-frequency warm shallow water acoustic communications channel model and measurements[J].Journal of Acoustical Society America，2007,，122(5)：2580-2586.

[6] BREKHOVSKIKH L M,，LYSANOV Y P.Fundamentals of ocean acoustics[M].New York：Springer,，2002.

[7] STOJANOVIC M.Underwater acoustic communications：design considerations on the physical layer[M].London：5th Annu Conf Wireless Demand Netw Syst Services，2008.

[8] DOMINGO M C.Overview of channel models for underwater wireless communication networks[J].Physical Communication,，2008,，1(3)：163-182.

[9] BOUVET P G，LOUSSERT A.Capacity analysis of under-water acoustic MIMO communications[M].Sydney：IEEE OCEANS,，2010.

[10] HICHERI R,，P?魧TZOLD M,TALHA B，et al.A study on the distribution of the envelope and the capacity of underwater acoustic channels[M].Macau.：IEEE International Conference on Communication Systems(ICCS),，2014.

[11] TEAL P D,，ABHAYAPALA T D，KENNEDY R A.Spatial correlation in non-isotropic scattering scenarios[C].2002 IEEE International Conference on Acoustics,，Speech,，and Signal Processing，2002：III-2833-III-2836.

[12] CHO Y,，LEE J H.Effect of fading correlation on the SER performance of M-ary PSK with maximal ratio combining[J].IEEE Communications Letters,，1999，3(7)：199-201.

[13] LOYKA S L.Channel capacity of MIMO architecture using the exponential correlation matrix[J].Communications Letters,，IEEE,，2001，5(9)：369-371.

[14] ZHOU Z,，ISHIZAWA K，KIKUCHI H,，et al.Generalized spatial correlation equations for antenna arrays in wireless diversity reception exact and approximate analyses[C].Proceedings of the 2003 International Conference on Neural Networks and Signal Processing,，2003..IEEE，2003,，1：180-184.

作者信息:

吳  鵬1,，周  杰1，2,，陳姜高路1,，菊池久和2

（1.南京信息工程大學(xué) 電子與信息工程學(xué)院，江蘇 南京210044,；

2.日本國立新瀉大學(xué) 工學(xué)部電氣電子工學(xué)科,，日本 新瀉950-2181)