0 引言

    隨著信息技術(shù)的不斷發(fā)展，信息安全已成為全世界的熱門研究課題,，而數(shù)據(jù)的有效加解密則顯得尤為重要,。雖然國內(nèi)外研究者在軟件加密層面上做了大量的工作，但仍存在著信息易被竊取等問題,。相對而言,，硬件加密因為其加解密過程在硬件中執(zhí)行，加解密信息均存儲于專用硬件之中^[1],，使得其更具安全性,。因此，研究加解密系統(tǒng)的硬件實現(xiàn)更具有現(xiàn)實意義,。

    LFSR偽隨機序列作為一種成熟流密碼,，其優(yōu)點突出，且非常適合于硬件高速實現(xiàn)^[2],。FPGA采用流水線和并行運算,，在數(shù)據(jù)處理中具有靈活高效的特點，很適合于硬件加解密系統(tǒng)的設(shè)計與實現(xiàn)^[3],。

    雖然利用LFSR序列進行加解密的硬件實現(xiàn)已有大量實例,，但其均為同步加解密，具有很大的局限性,。本文所提出的異步LFSR加解密系統(tǒng)即是針對這一問題而作出的改進,。首先對LFSR偽隨機序列產(chǎn)生的基本原理進行了闡述；然后分析了一種基于LFSR偽隨機序列的同步加解密系統(tǒng)；在此基礎(chǔ)之上,，提出了可配置的LFSR異步加解密系統(tǒng)的設(shè)計及其利用FPGA的實現(xiàn),，最后對全文進行了總結(jié)。

1 LFSR原理簡介

    一個m位的線性移位寄存器(LFSR)可以由m個寄存器以及決定序列狀態(tài)轉(zhuǎn)換的反饋結(jié)構(gòu)組成,。用于硬件實現(xiàn)的LFSR的拓撲結(jié)構(gòu)如圖1所示,。

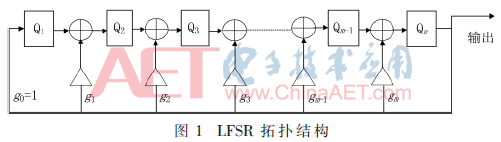
    該拓撲結(jié)構(gòu)中g(shù)_m代表反饋系數(shù)，其值為1表示連接,，0表示未連接,。每一時刻的各位寄存器的輸出則為當前的序列輸出值，下一時刻的輸出由當前狀態(tài)和反饋支路決定,。其數(shù)學抽象形式可以表示為GF(2^m)上的一個多項式,，反饋系數(shù)則抽象成為其多項式的系數(shù)。如果反饋系數(shù)選取得當,，使得其抽象多項式為GF(2^m)上的本原多項式時,，由m個寄存器組成的序列發(fā)生器可以有2^m-1個不同狀態(tài)^[4]。所以,，當m的值增大時,，該偽隨機序列發(fā)生器的周期增長是非常可觀的,，在一個周期之內(nèi),，其序列輸出值不可預(yù)測，保證了其安全性,，從而確保了加密效果,。

2 現(xiàn)有的同步LFSR加解密系統(tǒng)

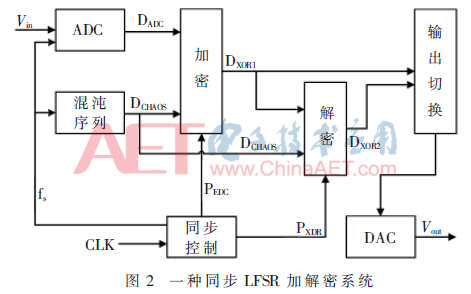
    現(xiàn)有的這方面的一個典型系統(tǒng)工作原理^[5]如圖2所示。該系統(tǒng)設(shè)計用LFSR偽隨機序列來加解密輸入模擬信號,。其基本原理是將輸入待加密的明文信號與LFSR序列進行兩次異或來加解密,，用m、k,、c分別來表示明文,、密鑰,、密文,，則由于：

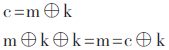
所以第一次異或?qū)⒚魑男畔⒓用埽诙萎惢騽t將密文解密,，得出明文信號,。整個過程的關(guān)鍵在于時序的控制使其達到嚴格同步。該系統(tǒng)結(jié)構(gòu)清晰,，原理明確,。但有幾點缺陷：

    (1)系統(tǒng)只在同步時可以進行工作，然而大多數(shù)情況之下這種即時加解密的方法不能滿足需求。而需要先加密,，傳輸,，之后再解密。

    (2)由于系統(tǒng)的加解密結(jié)構(gòu),，使得一幀數(shù)據(jù)加解密工作要在一個LFSR序列信號周期內(nèi)完成,，將限制時鐘頻率、降低效率,。

    (3)由于該系統(tǒng)需要加解密序列嚴格同步,，所以容錯率低，且只要出現(xiàn)一位的偏移將影響整個系統(tǒng),。

    對于以上問題,，本文提出了一種可配置LFSR序列異步加解密系統(tǒng)，將在下文討論,。

3 可配置的LFSR序列加解密系統(tǒng)

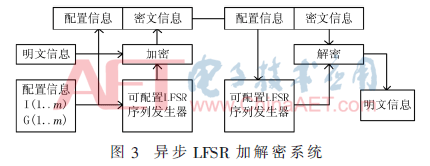
    針對現(xiàn)有LFSR同步加解密系統(tǒng)所存在的問題,，設(shè)計了一種異步加解密系統(tǒng)。該系統(tǒng)將在加密之前對LFSR進行配置,，設(shè)置其初值和反饋結(jié)構(gòu),。傳輸數(shù)據(jù)時將初值信號與反饋的配置信息封裝于密文之前，解密時再根據(jù)其接收到的密文中的配置信息進行解密端配置,，然后進行解密,。整個過程將實現(xiàn)異步加解密，其結(jié)構(gòu)如圖3所示,。

    其中最關(guān)鍵的部分為可配置LFSR序列發(fā)生器，其總體結(jié)構(gòu)如圖4所示,。

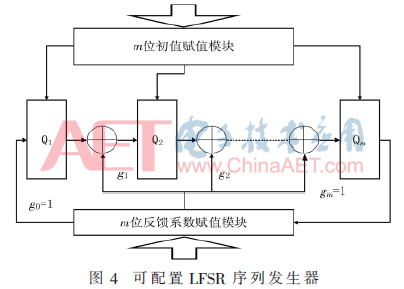
    對于m位的LFSR序列產(chǎn)生器,，其整體的配置模塊為m個單個配置結(jié)構(gòu)的并聯(lián),。單個寄存器的配置器如圖5所示,。其中初值賦值部分為寄存器賦初值,，而反饋系數(shù)賦值部分則用來配置反饋網(wǎng)絡(luò),。

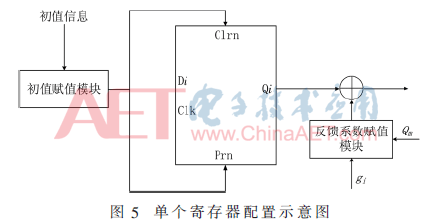
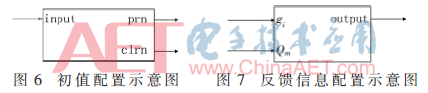
    其中初值配置模塊如圖6所示,。它接收初值信號，當初值為1,，即input為1時,，prn輸出0,，clrn輸出1，完成寄存器的置1設(shè)置,。反之,，當初值為0時,，clrn輸出0，prn輸出1,，完成寄存器的置0設(shè)置,。

    其中反饋結(jié)構(gòu)配置模塊如圖7所示。其接收到的輸入信號為Q_m與g_i,，且當g_i為1時，表示連接,，output輸出Q_m的值，當g_i為0時,，表示未連接,，則output輸出為0，因為x0=x,，與無連接的效果一樣。

4 加解密系統(tǒng)控制流程

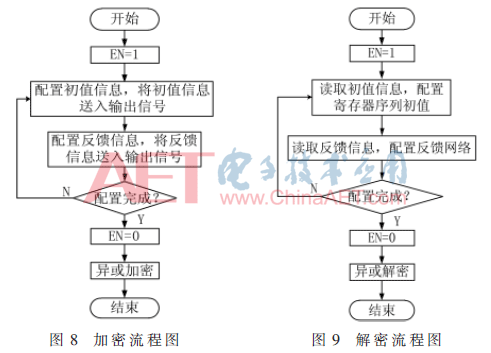
    基于前文所述的硬件結(jié)構(gòu),，設(shè)計了整個加解密系統(tǒng)的工作流程,，其加密與解密流程相對稱,，分別如圖8和圖9所示,。

5 系統(tǒng)仿真及測試結(jié)果

5.1 系統(tǒng)仿真時序圖

    圖10為可配置LFSR加解密裝置的加密過程仿真時序圖。仿真所用的LFSR生成器為8位,，其最大周期為255。選用的反饋系數(shù)為g(8)=01110001（由于g₀默認為1,，故從g₁開始配置）。

    Reset信號觸發(fā)之后,，EN為初始配置信號變?yōu)橛行?，其占?個時鐘周期,，完成的工作為將初始的配置信息中的Q⁰=10011100(156)與g(8)=01110001(q的ASCII碼)存入輸出信號cout,，并配置LFSR生成器。當配置結(jié)束后,，加密工作開始進行,。輸出密文c為明文m與LFSR輸出密鑰k的異或,，最終輸出cout為加入配置信息的密文,。相應(yīng)地,，其解密過程的仿真時序圖如圖11所示,。

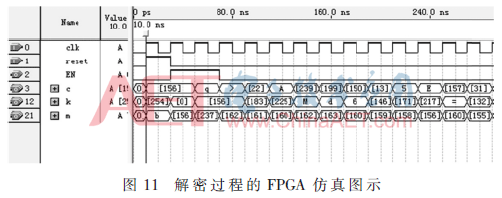
    Reset信號觸發(fā)之后,，初始配置信號EN變?yōu)橛行?，其占?個時鐘周期,，完成的工作為將接收到密文c中的前兩幀數(shù)據(jù)讀出,，并配置LFSR生成器,。當配置結(jié)束后,，解密工作開始進行,，解密輸出的明文從EN無效后開始,。由圖10、圖11所示,，其加解密過程都可以完美運行,。

5.2 實際加解密測試結(jié)果

    用上述加解密裝置對一幅512×512的灰度圖像進行加密,、解密可得其結(jié)果分別如圖12,、圖13所示,。可見加解密效果完美,，可以實際使用。

6 結(jié)語

    本文設(shè)計了一種可配置的LFSR序列生成器以及其所應(yīng)用的異步加解密裝置。在對原始LFSR加解密系統(tǒng)進行了闡述與分析后,，提出了一種可配置的LFSR異步加解密系統(tǒng)，并對其進行了基于FPGA的硬件實現(xiàn),。觀察實驗結(jié)果可知,，其不僅具有異步加解密的實用性,，又具有LFSR序列的可靠性,。

參考文獻

[1] 賈立愷,，黃國慶，趙敬,，等.基于FPGA的PCI硬件加解密卡設(shè)計[J].電子設(shè)計工程,，2010，18(5)：142-145.

[2] 胡向東.應(yīng)用密碼學[M].北京：電子工業(yè)出版社,，2011.

[3] 劉景亞,，季曉勇.基于FPGA的CPRS混沌加解密算法高效實現(xiàn)[J].電子測量技術(shù)，2008,，31(11)：175-177.

[4] WADE TRAPPE(美).密碼學與編碼理論(第2版)[M].北京：人民郵電出版社,，2008.

[5] 劉衛(wèi)玲，常曉明,，王云才.基于FPGA和PSoC的混沌音頻加解密系統(tǒng)[J].電子技術(shù)應(yīng)用,，2014，40(7)：54-57.