0 引言

    SFM(Sinusoidal Frequency Modulation)信號(hào)是一種典型的非平穩(wěn)信號(hào),，具有頻率時(shí)變,、低截獲概率等性質(zhì)，在雷達(dá),、聲納,、生物醫(yī)學(xué)及地震信號(hào)處理等領(lǐng)域得到廣泛應(yīng)用^[1]。傳統(tǒng)的傅里葉變換是信號(hào)分析與處理的重要技術(shù)手段，但不能反映非平穩(wěn)信號(hào)頻率的時(shí)變本質(zhì),，而時(shí)頻分析^[2-3]注重信號(hào)時(shí)變譜特征,，描述信號(hào)隨時(shí)間和頻率的能量分布。因此,，研究SFM信號(hào)的時(shí)頻分析方法具有重要的意義,。

    近年來(lái)，時(shí)頻分析方法在非平穩(wěn)信號(hào)處理領(lǐng)域中引起廣泛關(guān)注和研究,，主要應(yīng)用于雷達(dá)目標(biāo)探測(cè),、語(yǔ)音信號(hào)和圖像處理、生物信號(hào)診斷等領(lǐng)域,。Wigner-Ville分布(WVD)是分析非平穩(wěn)時(shí)變信號(hào)的重要工具之一,，是一種基本Cohen類雙線性時(shí)頻分布，具有很好的時(shí)頻聚集性^[4],，但對(duì)于非線性調(diào)頻信號(hào)會(huì)產(chǎn)生交叉項(xiàng)干擾,。偽Wigner-Ville分布(PWVD)能夠抑制交叉項(xiàng)干擾，但降低了時(shí)頻分辨率,，且改變了邊緣性質(zhì)^[5],。1993年，MALLAT和ZHANG^[6]首次提出在過完備字典中對(duì)信號(hào)進(jìn)行稀疏分解的思想,，并引入了匹配追蹤(Matching Pursuit,，MP)算法,。目前,，稀疏分解被廣泛應(yīng)用到信號(hào)處理的許多方面，如編碼,、去噪,、微弱信號(hào)提取等，但在時(shí)頻分析中的研究甚少,。文獻(xiàn)[7]利用Gabor原子對(duì)語(yǔ)音信號(hào)進(jìn)行分解,，很好地利用了Gabor原子來(lái)表示信號(hào)的內(nèi)在結(jié)構(gòu)；文獻(xiàn)[8]將MP分解方法應(yīng)用在雷達(dá)目標(biāo)識(shí)別中,，該方法雖然提高了原子的搜索效率,，但本質(zhì)上沒有降低信號(hào)分解的計(jì)算復(fù)雜度，難以實(shí)現(xiàn)信號(hào)實(shí)時(shí)處理,。

    為解決SFM信號(hào)WVD存在的時(shí)頻交叉項(xiàng)干擾問題,，本文提出一種基于稀疏分解的時(shí)頻分析方法。該方法首先在Gabor原子字典中對(duì)信號(hào)進(jìn)行MP分解,，然后將分解得到的Gabor原子通過Wigner-Ville變換疊加得到信號(hào)WVD,。仿真結(jié)果表明，本文方法能提高對(duì)信號(hào)分解的計(jì)算效率,，不僅能抑制交叉項(xiàng)干擾,，還能保持高時(shí)頻分辨率,，是一種有效的時(shí)頻分析方法。

1 SFM信號(hào)模型及時(shí)頻特性分析

1.1 SFM信號(hào)模型

    SFM信號(hào)的頻率特性曲線是關(guān)于時(shí)間的正弦函數(shù),，其數(shù)學(xué)模型為：

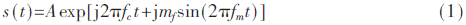
式中,，A為SFM信號(hào)的幅度，f_c為載頻,，f_m為調(diào)制頻率,，m_f為調(diào)制指數(shù)。由于瞬時(shí)頻率是瞬時(shí)相位關(guān)于時(shí)間的導(dǎo)數(shù),，則：

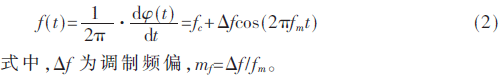
1.2 時(shí)頻特性分析

    信號(hào)s(t)的Wigner-Ville變換定義為：

    由式(4)可知,，當(dāng)信號(hào)相位關(guān)于時(shí)間的二階以上導(dǎo)數(shù)為零時(shí)，如線性調(diào)頻信號(hào)WVD不含交叉項(xiàng),，表現(xiàn)出最佳時(shí)頻聚集性,；當(dāng)信號(hào)相位關(guān)于時(shí)間的二階以上導(dǎo)數(shù)不為零時(shí)，由于其高次項(xiàng)的作用,，信號(hào)WVD會(huì)產(chǎn)生自身交叉項(xiàng),。為了解決SFM信號(hào)的交叉干擾問題，本文將利用Gabor原子的時(shí)頻特性,，聯(lián)合稀疏分解和WVD的方法對(duì)SFM信號(hào)進(jìn)行分析,。

2 基于稀疏分解的時(shí)頻分析方法

2.1 Gabor原子字典的構(gòu)建及離散化

    Gabor原子的數(shù)學(xué)表示式為：

    對(duì)于由Gabor原子所構(gòu)成的字典，首先將g_γ作歸一化處理,，即||g_γ||=1,，然后根據(jù)Mallat索引算法對(duì)信號(hào)的時(shí)頻參數(shù)進(jìn)行離散化。

    由圖1可知,，隨著j的遞增位移參數(shù)的掃描間隔不斷變得稀疏,，而頻率參數(shù)的掃描間隔不斷變得密集。在迭代過程中,，先根據(jù)j值確定時(shí)頻參數(shù)的取值范圍和步距,，再依次掃描時(shí)頻參數(shù)來(lái)選取最相關(guān)的原子參數(shù)。

2.2 聯(lián)合MP分解和WVD的時(shí)頻分析

    假設(shè)D為N維Hilbert空間H中的Gabor原子字典,，g_γ為由參數(shù)組γ定義的Gabor原子,。考察逼近任意信號(hào)f,，信號(hào)長(zhǎng)度為N,，則信號(hào)可被分解為：

其中α為優(yōu)化因子，0<α≤1,。為了尋找與分解的殘余最為匹配的原子,，取α=1。

    當(dāng)殘余能量低于一定閾值或者滿足一定的迭代次數(shù)時(shí)，該迭代過程結(jié)束,。由式(7)可得,，用少量Gabor原子即可表示信號(hào)的主要成分，即：

式(10)和M<<N集中體現(xiàn)信號(hào)稀疏表示的思想,，它代表信號(hào)稀疏分解的結(jié)果,。

    對(duì)每次迭代過程中分解得到的Gabor原子進(jìn)行Wigner-Ville變換，由式(12)得到信號(hào)WVD：

3 利用改進(jìn)遺傳算法尋找最佳匹配原子

    基于MP的稀疏分解算法存在的關(guān)鍵問題是計(jì)算量大,。本文采用分層思想對(duì)傳統(tǒng)遺傳算法(GA)尋找最佳匹配原子進(jìn)行改進(jìn),。利用過完備原子庫(kù)“波形相同”的等價(jià)關(guān)系[9]，對(duì)字典D按式(13)進(jìn)行劃分：

    將定義一個(gè)原子的參數(shù)組作為待尋優(yōu)參數(shù),，殘余與最佳匹配原子內(nèi)積的絕對(duì)值作為適應(yīng)度函數(shù),。當(dāng)每個(gè)子庫(kù)運(yùn)行到一定代數(shù)時(shí)，將N個(gè)子庫(kù)結(jié)果和平均適應(yīng)度分別記錄到數(shù)組R[i,，j](i=1,，…，N,；j=1,，…，n)和A[i]中,，進(jìn)行選擇,、交叉和變異操作，淘汰適應(yīng)度值低的原子,，然后更新R[i,，j]和A[i]，并開始新的分解迭代過程,。利用改進(jìn)遺傳算法尋找最佳匹配原子如圖2所示,。

4 仿真及性能分析

    仿真實(shí)驗(yàn)中，采用SFM信號(hào),，信號(hào)長(zhǎng)度為N=140，s(t)=exp[j0.5πt+j20sin(0.02πt)],。為便于信號(hào)分析和處理,，對(duì)采樣頻率進(jìn)行歸一化處理。由文獻(xiàn)[7]可知,，當(dāng)信號(hào)長(zhǎng)度為140時(shí),，字典中含有59 129個(gè)Gabor原子，滿足原子字典的過完備性,。

    圖3,、圖4分別為SFM信號(hào)的WVD和PWVD。由圖可知，SFM信號(hào)WVD存在嚴(yán)重的交叉項(xiàng),，與理論分析相符,；其PWVD雖抑制了交叉項(xiàng)，具有較好的聚集性,，但降低了時(shí)頻分辨率,，改變了邊緣性質(zhì)。

4.1 實(shí)驗(yàn)一：正弦調(diào)頻信號(hào)的稀疏分解

    對(duì)SFM信號(hào)在Gabor原子字典中做稀疏分解,，迭代次數(shù)為200,。圖5表示Gabor原子示意圖，Gabor原子的能量較為集中,，這種集中的特性是由信號(hào)時(shí)頻參數(shù)構(gòu)成的Gabor原子是一個(gè)高斯窗函數(shù),，具有代表性。

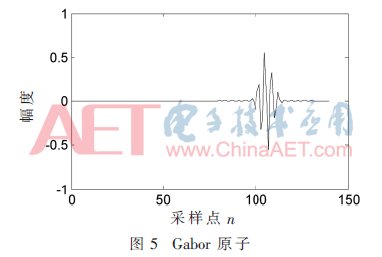
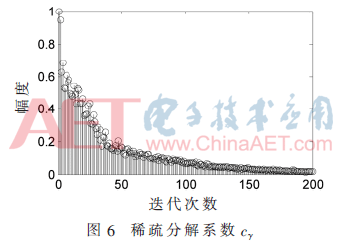
    圖6和圖7分別表示SFM信號(hào)在200次迭代過程中分解系數(shù)的變化及逼近誤差,。隨著迭代次數(shù)的增加,，分解系數(shù)幅值不斷減小，表明在分解的過程中殘余能量越來(lái)越?。ń?jīng)過200次分解后逼近誤差值小于0.05）,，重構(gòu)信號(hào)越來(lái)越逼近原SFM信號(hào)。

4.2 實(shí)驗(yàn)二：時(shí)頻特性分析

    通過改變迭代次數(shù)來(lái)比較由不同原子數(shù)構(gòu)建信號(hào)的WVD,。圖8,、圖9分別表示為由30、50個(gè)Gabor原子構(gòu)建信號(hào)的WVD,，顏色表示信號(hào)能量分布,。由圖可知，Gabor原子在時(shí)頻圖上表現(xiàn)為時(shí)頻塊,，具有最佳的時(shí)頻聚集性,，信號(hào)WVD是由一系列Gabor原子組合得到。仿真結(jié)果表明,，本文方法有效抑制了SFM信號(hào)WVD的交叉項(xiàng)干擾,，并保持高的時(shí)頻分辨率。

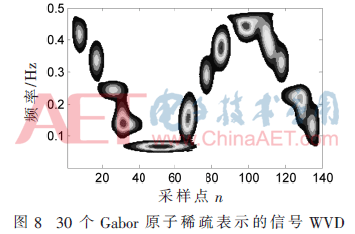
    經(jīng)過多組測(cè)試,，不同Gabor原子數(shù)構(gòu)建信號(hào)WVD的效果不同,，說明信號(hào)的稀疏表示存在多種形式；同時(shí)在本文給出的參數(shù)條件下,，采用35個(gè)Gabor原子構(gòu)成信號(hào)的WVD效果最好,。

4.3 實(shí)驗(yàn)三：稀疏分解性能分析

    設(shè)種群進(jìn)化代數(shù)為35，染色體個(gè)數(shù)為21,。從算法復(fù)雜度角度來(lái)看,，稀疏分解計(jì)算復(fù)雜度取決于殘余與最佳匹配原子的內(nèi)積運(yùn)算量,。假設(shè)基于MP分解計(jì)算速度為1，3種不同分解方法的相對(duì)計(jì)算速度及均方根誤差比較如表1所示,，以重構(gòu)信號(hào)與原信號(hào)之間的均方根誤差(RMSE)作為衡量重構(gòu)信號(hào)質(zhì)量的標(biāo)準(zhǔn),。

    由表1可知，3種方法得到的RMSE均小于-19 dB,，說明35個(gè)Gabor原子可很好地重構(gòu)原信號(hào)相對(duì)基于MP分解和GA的MP分解方法而言,，本文方法在保證重構(gòu)信號(hào)質(zhì)量的情況下，提高了稀疏分解的計(jì)算效率,。

5 結(jié)束語(yǔ)

    從稀疏分解的角度出發(fā),，本文提出一種聯(lián)合稀疏分解和Wigner-Ville分布的時(shí)頻分析方法。在傳統(tǒng)時(shí)頻分析方法的基礎(chǔ)上,，本文利用Gabor原子的時(shí)頻特性,，將信號(hào)WVD用一系列最佳匹配Gabor原子的WVD疊加得到。相對(duì)于信號(hào)的時(shí)頻分布,，稀疏分解得到的是與信號(hào)最為匹配原子的參數(shù)信息,，靈活地選取Gabor原子，可以更為稀疏地表示信號(hào),，有效地揭示了非平穩(wěn)信號(hào)的時(shí)頻結(jié)構(gòu),，其不但是稀疏的，而且可以方便應(yīng)用于進(jìn)一步的信息處理,。

參考文獻(xiàn)

[1] 李英祥．低截獲概率信號(hào)非平穩(wěn)處理技術(shù)研究[D]．成都：電子科技大學(xué),，2003.

[2] 鄒紅星，周小波,，李衍達(dá).時(shí)頻分析：回溯與前瞻[J].電子學(xué)報(bào),，2000，28(9)：78-84.

[3] COHEN L.Time-frequency analysis[J].Upper Saddle River,，NJ：Prentice-hall,，1995，181(2)：335-337.

[4] QIAN S,，CHEN D.Joint time-frequency analysis[J].IEEE Signal Processing Magazine,，1999，16(2)：52-67.

[5] 葛哲學(xué),，陳仲生.Matlab時(shí)頻分析技術(shù)及其應(yīng)用[M].北京：人民郵電出版社,，2006.

[6] MALLAT S G，ZHANG Z.Matching pursuits with time-frequency dictionaries[J].IEEE Transactions on Signal Processing,，1993，41(12)：3397-3415.

[7] LOBO A P,，LOIZOU P C.Voiced unvoiced speech discri-mination in noise using gabor atomic decomposition[C].IEEE International Conference on Acoustics,，Speech and Signal Processing,，2003，1：820-823.

[8] 段沛沛,，李輝.快速稀疏分解在雷達(dá)目標(biāo)識(shí)別中的應(yīng)用[J].電子技術(shù)應(yīng)用,，2015，41(7)：64-67.

[9] 邵君,，尹忠科,，王建英.信號(hào)稀疏分解中過完備原子庫(kù)的集合劃分[J].鐵道學(xué)報(bào)，2006,，28(1)：68-71.