劉清華,，楊桂芹，張妍妮

　?。ㄌm州交通大學(xué) 電子與信息工程學(xué)院,，甘肅 蘭州 730070）

　　摘要：隨著數(shù)據(jù)采集能力和采樣頻率的不斷提高，采用傳統(tǒng)的奈奎斯特采樣定理會獲得海量的數(shù)據(jù),，這給信號的存儲和傳遞帶來了極大挑戰(zhàn),。提出基于稀疏快速傅里葉變換的信號壓縮方法，利用信號在頻域的稀疏性,，壓縮信號所需的存儲空間,，在保證擁有足夠小的誤碼率的前提下，以高概率重構(gòu)原始信號,。

　　關(guān)鍵詞：稀疏快速傅里葉變換,；信號壓縮；重構(gòu)

0引言

　　傳統(tǒng)的信號離散化基本依據(jù)——奈奎斯特采樣定理認(rèn)為,，在進(jìn)行模擬/數(shù)字信號的轉(zhuǎn)換過程中,，當(dāng)采樣頻率大于信號中最高頻率的2倍時，采樣之后的數(shù)字信號完整地保留了原始信號中的信息,，而實(shí)際應(yīng)用中一般需要5～10倍才能達(dá)到理想的效果,。然而，近十幾年傳感系統(tǒng)獲取數(shù)據(jù)的能力不斷增強(qiáng),，采樣頻率越來越高,，需要處理的數(shù)據(jù)量也不斷增多，這就給信號處理的能力提出了更高的要求,。

　　2012年,，麻省理工學(xué)院（Massachusetts Institute of Technology, MIT）的4位研究員提出了一種新的信號處理算法——稀疏快速傅里葉變換（Sparse Fast Fourier Transform,，SFFT）［12］。它通過利用信號頻域的稀疏特性,，以與信號長度成亞線性關(guān)系的時間復(fù)雜度及高概率重構(gòu)出信號完整頻譜,，其效率是傳統(tǒng)快速傅里葉變換（Fast Fourier Transform, FFT）算法的10～100倍。

1稀疏快速傅里葉變換理論

　　離散傅里葉變換（Discrete Fourier Transform, DFT）作為一種重要的變換手段被廣泛應(yīng)用于信號處理,、通信,、音頻/圖片/視頻的壓縮等領(lǐng)域。FFT作為實(shí)現(xiàn)DFT變換最快速的方法而被廣泛使用,，對n維信號的FFT時間復(fù)雜度為O(nlogn),。

　　但在實(shí)際應(yīng)用中，大部分的傅里葉系數(shù)很小或者等于0,，只有少部分的系數(shù)是不可忽略的,，而這少部分系數(shù)正是信號恢復(fù)中必不可少頻率值。如果對信號不假思索地使用FFT處理,，那么就會花費(fèi)大量的運(yùn)算時間在并不關(guān)心的零頻點(diǎn)上,。

　　對n維離散信號，參考文獻(xiàn)［2］中指出：

　?。?）若信號為精確k稀疏信號,，則SFFT的時間復(fù)雜度為O(klogn)；

　?。?）若信號為一般信號,，則SFFT的時間復(fù)雜度為O(klognlog(n/k))。

　　對于任意k∈Rn,，兩種情況都比FFT要快,。

　　1.1SFFT理論框架

　　圖1SFFT理論框圖SFFT是利用信號頻譜的稀疏性來降低DFT運(yùn)算的復(fù)雜度的算法，其理論框圖如圖1所示,。SFFT算法是將數(shù)量為n的信號頻率系數(shù)按規(guī)律H投入B個“筐”中,。因?yàn)樾盘栐陬l域是稀疏的，所以每個框中很高的概率只會分得一個大系數(shù),。如此便將長度為n的信號轉(zhuǎn)換成了長度為B的信號了,，且Bn。對變換后的信號做B點(diǎn)FFT,。最后設(shè)計(jì)重構(gòu)算法H－1恢復(fù)出大頻率系數(shù)的位置和幅值,，從而得到原始信號的頻譜。

　　1.2SFFT相關(guān)數(shù)學(xué)符號

　　設(shè)信號x∈Cn,，其中n為信號的長度且n=2a（a為正整數(shù)）,，信號x的傅里葉頻譜為。k表示信號稀疏度,。x*y表示x與y的卷積,，x·y表示x與y的乘積,，即有x·y=*。supp(x)表示x的一個支撐集,，即x非零坐標(biāo)的集合,。本文定義ω=e2πi/n。

　　1.3頻譜重排

　　參考文獻(xiàn)［3］中指出,，信號在時域的二次采樣會引起頻域的頻譜混疊,。因此，可以通過時域的二次采樣達(dá)到頻譜重排的效果,，從而降低頻譜長度,。設(shè)傳遞函數(shù)為Pσ,τ，其中σ為奇數(shù)且對n的取模運(yùn)算可逆,，整數(shù)τ∈［n］,。可得

　　故,，換元得到時域重排后引起頻域變化的公式為：

　　參考文獻(xiàn)［1］指出,，如果j≠0，n為2的整數(shù)次冪，且σ∈［n］是一個均勻隨機(jī)奇數(shù)時,，則大傅里葉系數(shù)落在同一個“筐”中的概率為：

　　P{σj∈［－C,C］}≤4C/n

　　如果n不是2的整數(shù)次冪,，就在信號后邊添加若干個0，使其長度為2的整數(shù)次冪,。

　　1.4平滑濾波器

　　數(shù)字信號處理領(lǐng)域擁有多種類型的濾波器，濾波器可以將感興趣的部分從原始信號中分離出來，進(jìn)而進(jìn)行特殊處理,。在SFFT算法中需要一個時域和頻域的能量都集中且其通帶和阻帶紋波較小的濾波器。滿足上述要求的首推理想低通濾波器,，但在實(shí)際中理想低通濾器無法實(shí)現(xiàn),，通常通過截?cái)嗖⒕矸e其他窗函數(shù)而實(shí)現(xiàn)。時域的Sinc(·)函數(shù)其頻域?yàn)榫匦未昂瘮?shù),，截?cái)嗪笥捎谄鋾r域的不連續(xù)性導(dǎo)致截?cái)嗪蟮念l域響應(yīng)在通帶和阻帶出現(xiàn)了明顯的紋波,。參考文獻(xiàn)［4］指出，凱澤窗和道爾夫切比雪夫窗可以控制通帶和阻帶的紋波,。因此,，本文的平滑濾波器采用截?cái)嗪蟮腟inc(·)與道爾夫切比雪夫窗卷積的方式實(shí)現(xiàn)。以下給出具體實(shí)現(xiàn)過程,。

　　定義：設(shè)F(ε,δ,w)∈Rn為定義域內(nèi)的一組對稱序列,，若F滿足：

　　則稱F為標(biāo)準(zhǔn)窗函數(shù)。

　　參考文獻(xiàn)［1］指出,，對于任意給定阻帶截?cái)嘁蜃应藕驼鹗幖y波δ,，總可以構(gòu)造出一個標(biāo)準(zhǔn)窗函數(shù):

　　但是,，這個標(biāo)準(zhǔn)窗函數(shù)只規(guī)定了阻帶特性，在通帶內(nèi)仍然有較大的紋波,，影響算法效率,。

　　定義：設(shè)F(ε,ε′,δ,w)∈Rn為定義域內(nèi)的一組對稱序列，若F滿足:

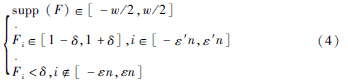
　　則稱F為平滑窗函數(shù),，其中ε′為通帶截?cái)嘁蜃?，其他符號與公式（3）相同。

　　本文采用道爾夫切比雪夫窗與矩形窗函數(shù)卷積生成平滑濾波器,，用符號G表示,。當(dāng)然用凱澤窗代替道爾夫切比雪夫窗也可以實(shí)現(xiàn)平滑濾波器，這里不再贅述,。

　　將時域重排的信號通過平滑濾波器,，生成函數(shù)y=G·(Pσ,τx)，所以：

　　yi=Gixσi+τ,，supp(y)supp(G)=［w］（5）

　　由平滑濾波器的設(shè)計(jì)過程可知,，只需要確定信號長度n和稀疏度k便可構(gòu)造出平滑濾波器，這與信號具體內(nèi)容無關(guān),。所以濾波器的設(shè)計(jì)可以在算法執(zhí)行前的預(yù)處理階段完成,，這樣不僅降低了算法的運(yùn)算量，同時不必將濾波器數(shù)據(jù)傳輸?shù)浇邮斩?，提高了?shù)據(jù)壓縮比,。

　　1.5頻域降采樣

　　由公式（5）知信號y∈Cw，設(shè)“筐”的數(shù)量為B,，且B整除信號長度w?，F(xiàn)令：

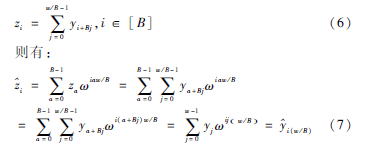
　　可見，時域的混疊造成了頻域的等間隔采樣,，即頻域降采樣［5］,。

　　1.6重構(gòu)算法

　　重構(gòu)過程主要分為3步：哈希映射、定位循環(huán)和估值循環(huán),。

　　設(shè)哈希映射函數(shù)為hσ(i)=round(σiB/n),，它確定了分“筐”的規(guī)則。同時設(shè)偏移量向量oσ(i)=σi－h(huán)σ(i)(n/B),，它確定了估值循環(huán)時濾波器的坐標(biāo),。定位循環(huán)得到i中最大的前dk個值的坐標(biāo)J，經(jīng)過哈希函數(shù)反映射得到J的原像I={i∈［n］|hσ(i)∈J},。對于i∈I,，由′i=hσ(i)ωτi/oσ(i)得到原始信號x的逼近值。

　　因?yàn)槠交瑸V波器通帶幾乎平滑,，阻帶以指數(shù)衰減,，所以相鄰大值點(diǎn)之間的頻譜泄露可以忽略,。因此，重構(gòu)算法不需要迭代,，結(jié)構(gòu)簡單［6］,。此外，為協(xié)調(diào)“分筐”的開銷和重構(gòu)估值的開銷,，取參數(shù)B≈n·k,，且B整除n。

　　2SFFT算法信號壓縮的仿真與評價

　　為驗(yàn)證算法的可行性,，本文構(gòu)建了多個不同參數(shù)的一維稀疏信號,，在長度為n的信號中，均勻隨機(jī)選取k個位置為非零值,，其余設(shè)置為零值,。在算法耐噪聲測試中，采用高斯白噪聲作為信號傳遞過程中的信道噪聲,。

　　圖2是其中一個測試用例的原始信號和恢復(fù)信號對比圖,，其信號長度為65 536，頻域稀疏度為50,，信道信噪比為20 dB,。從圖中可以看出即使較小的頻點(diǎn)幅值依然可以高概率重構(gòu)出來。

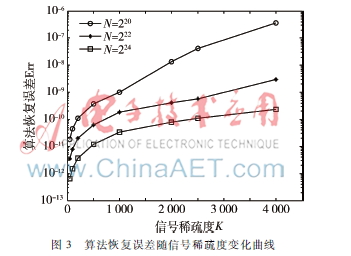
　　圖3是描述算法重構(gòu)誤差隨信號稀疏度的變化曲線,。選取測試用例中信號長度分別為220,、222,、224,、稀疏度在50～4 000之間變化的測試信號。由圖3可知當(dāng)信號長度一定時,，SFFT算法的恢復(fù)誤差隨稀疏度的增大而逐漸增大,；當(dāng)信號的稀疏度一定時，信號長度越長SFFT算法的恢復(fù)誤差越小,?？傊盘柕拇笙禂?shù)在信號中占的比例越大,，其恢復(fù)誤差就越大,；在大系數(shù)個數(shù)比較少的情況下，其算法的恢復(fù)誤差可以低于1×10-10,。

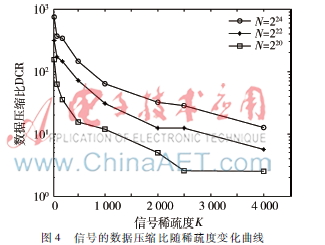
　　圖4是不同稀疏度的情況下SFFT算法的數(shù)據(jù)壓縮比變化曲線,。橫向比較可以看出，在信號長度一定的情況下,，其非零點(diǎn)越多,，在信道傳輸存儲所需的物理單元就越多,，則其數(shù)據(jù)壓縮比就越小。當(dāng)信號長度為224,、信號稀疏度為50的時候,，SFFT的數(shù)據(jù)壓縮比高達(dá)741.436；當(dāng)信號長度為224,、信號稀疏度為4 000的時候,，SFFT的數(shù)據(jù)壓縮比降到了12.722?？v向比較可以看出,，當(dāng)信號稀疏度一定的情況下，信號長度越長其壓縮比越大,。

3結(jié)論

　　本文通過通過分析傳統(tǒng)信號壓縮的不足,，提出一種基于稀疏快速傅里葉的信號壓縮方式。該方法通過利用信號頻域的稀疏特性,，成功降低了信號進(jìn)行傅里葉變換的長度,，在保證足夠小的誤碼率的情況下，使傳輸信號具有良好的數(shù)據(jù)壓縮比,，同時使計(jì)算傅里葉變換的時間大大縮短,。通過構(gòu)建參數(shù)不同的信號進(jìn)行SFFT算法仿真，證明該算法在信號壓縮方面擁有很大的優(yōu)勢,。

參考文獻(xiàn)

　?。?］ HASSANIEH H, INDYK P, KATABI D, et al. Simple and practical algorithm for sparse Fourier transform［C］. Proceedings of the TwentyThird Annual ACMSIAM Symposium on Discrete Algorithms， SIAM, 2012: 11831194.

　?。?］ HASSANIEH H, INDYK P, KATABI D, et al. Nearly optimal sparse Fourier transform［J］. Association for Computing Machinery, 2012:563578.

　?。?］ GILBERT A C, MUTHUKRISHNAN S, STRAUSS M. Improved time bounds for nearoptimal sparse Fourier representations［J］. Proceedings of SPIE, 2005, 5914:398412.

　　［4］ DINIZ P S R,， da SILVA E A B,， NETTO S L. 數(shù)字信號處理系統(tǒng)分析與設(shè)計(jì)(原書第2版)［M］. 張?zhí)劊袅臆?，于迎霞,，譯.北京: 機(jī)械工業(yè)出版社, 2013.

　　［5］ HSIEH S H, LU C S, PEI S C. Sparse fast Fourier transform by downsampling［C］. 2013 IEEE International Conference on Acoustics, Speech, and Signal Processing, 2013:56375641.

　?。?］ 那美麗, 周志剛, 李霈霈. 基于稀疏傅里葉變換的低采樣率寬帶頻譜感知［J］. 電子技術(shù)應(yīng)用, 2015, 41(11): 8588.