付永強,，宋麗華，李也白,馬禮
?。ū狈焦I(yè)大學 計算機學院,，北京 100144）
摘要：為了能夠?qū)崿F(xiàn)動態(tài)無灰度特征峰值的圖像分割，提出一種基于決策樹的神經(jīng)網(wǎng)絡(Decision Tree Based Neural Network,，DTBNN)雙閾值圖像分割方法,。該方法首先運用決策樹與神經(jīng)網(wǎng)絡的對應關系，構建出穩(wěn)定,、訓練高效的神經(jīng)網(wǎng)絡,；然后通過實驗采集的圖像提取圖像灰度均值，最大灰度偏差與閾值映射函數(shù)作為樣本數(shù)據(jù)訓練神經(jīng)網(wǎng)絡,；最后采用訓練好的神經(jīng)網(wǎng)絡對被測圖像進行閾值映射函數(shù)篩選,，并計算出被測圖像的上下灰度閾值,，完成對圖像的雙閾值分割。仿真實驗表明,，該方法不依賴于灰度直方圖的峰值特征并能獲取較好的上下限分割閾值,，與最大類間方差雙閾值法和最大熵雙閾值法比較，能夠在動態(tài)圖像中實現(xiàn)雙閾值分割,。
關鍵詞： DTBNN,；雙閾值；圖像分割
0引言
圖像分割技術的關鍵是將被識別物從背景環(huán)境中分離出來,，通常的分割方法有基于閾值,、基于邊緣提取和基于區(qū)域的圖像分割方法。其中以基于閾值的圖像分割方法最為常見,，因其算法簡單,、效率高而被廣泛應用于圖像處理中。閾值分割又可分為全局閾值分割和局部閾值分割,，其算法主要有最大類間方差法（又稱為Otsu法）,、最大熵法和模糊熵法。這些閾值分割算法可以采用單閾值和多閾值進行圖像分割,。由于單閾值圖像分割是用一個閾值將圖像劃分為兩個灰度級部分,，有時不能有效地將目標物體從圖像中分割出來。雙閾值圖像分割是通過劃分上限和下限并提出兩個閾值中間灰度域作為有效區(qū)域, 能夠更有效地將目標物體從圖像中分割出來,。
在雙閾值圖像分割算法中,，基于Otsu的雙閾值圖像分割及其改進算法［12］使用較為普遍，但是Otsu算法對圖像直方圖具有三峰特征值的圖像具有較好的分割結果,，而對其他情況下的圖像分割效果不佳,。基于最大熵的雙閾值圖像分割及其改進算法［3］,，由于其依據(jù)的是使圖像中目標與背景的總熵最大,，所以在圖像處理過程中仍然需要灰度直方圖中具有三峰值特征?；谀：丶捌涓倪M的雙閾值圖像分割算法［45］是通過隸屬度函數(shù)確定暗,、灰、亮三部分的范圍,，但在動態(tài)圖像中無法有效確定隸屬度函數(shù),，所以不能用于動態(tài)圖像分割。另外還有基于二分灰度直方圖的多閾值分割算法［6］,，此方法仍然建立在最大類間方差的基礎上,，對目標閾值的劃分也依賴于灰度直方圖的峰值特征。
在本文所提及的實際工程中,，需要對旋轉物體圖像提取有效特征信息,，但是由于環(huán)境光在旋轉面的反射成像,，隨著旋轉物體旋轉角度的不同，使得在采集的圖像中灰度直方圖變化較大且有時不存在明顯峰值特征,?；谝陨蠎帽尘昂蛯嶋H工程需要,，本文提出一種基于決策樹的神經(jīng)網(wǎng)絡（Decision Tree Based Neural Network, DTBNN)算法的雙閾值圖像分割方法,，該方法在實際應用中表現(xiàn)出良好的圖像分割效果。
1DTBNN算法
人工神經(jīng)網(wǎng)絡（Artificial Neural Network,，ANN）已經(jīng)被廣泛應用于識別和分類算法中,，其能夠通過有師學習或無師學習的方式，達到類似生物神經(jīng)網(wǎng)絡的信息處理和分類的效果,。本文中采用的BP（Back Propagation）神經(jīng)網(wǎng)絡,，即在前向神經(jīng)網(wǎng)絡的基礎上增加逆向?qū)W習能力，在本文中簡稱神經(jīng)網(wǎng)絡,。該模型是一種按誤差逆向傳播訓練的多層前饋網(wǎng)絡,，其網(wǎng)絡拓撲結構包括輸入層、隱層和輸出層,。通過最速下降法學習使得在神經(jīng)網(wǎng)絡中存儲大量的從輸入到輸出的映射關系,，建立好的神經(jīng)網(wǎng)絡通過這些映射關系可以對輸入信息做出推理和分類。在圖像識別的分類技術中也經(jīng)常用到神經(jīng)網(wǎng)絡,，如人臉識別,、分類篩選等，這些都是用以分類而滿足識別的,，但本文提出將訓練后的神經(jīng)網(wǎng)絡應用在圖像閾值函數(shù)的分類篩選過程中,。
由于神經(jīng)網(wǎng)絡結構和初始參數(shù)值在設計上較為困難，并嚴重影響網(wǎng)絡的性能,，李愛軍等人在深入研究SETHI I K的熵網(wǎng)絡［7］基礎上提出基于決策樹的神經(jīng)網(wǎng)絡（DTBNN）算法［8］,，并通過“異或”問題和多類問題驗證分析其有效性。決策樹算法是通過決策對象的屬性進行分類學習,；神經(jīng)網(wǎng)絡算法是通過神經(jīng)元之間的權重關系分類學習,。盡管兩者的機制不完全相同，但是決策樹與神經(jīng)網(wǎng)絡存在一定的對應關系,。李愛軍等人提出將決策樹的內(nèi)部節(jié)點數(shù)與神經(jīng)網(wǎng)絡的輸入層神經(jīng)元數(shù)相對應,，將決策樹的葉子節(jié)點數(shù)對應于隱層神經(jīng)元數(shù)，將決策樹的分類數(shù)對應于輸出層的神經(jīng)元數(shù),，將決策樹中的連接與神經(jīng)網(wǎng)絡的神經(jīng)元間連接相對應,，將決策樹中的連接權重與神經(jīng)網(wǎng)絡的連接權重相對應。圖1表示兩者之間的對應關系,，矩形表示決策樹,，橢圓形表示神經(jīng)網(wǎng)絡,。
根據(jù)圖1展示的對應規(guī)則，可以利用決策樹構造出神經(jīng)網(wǎng)絡的層次結構以及初始化參數(shù)值,。N個決策樹內(nèi)部節(jié)點對應神經(jīng)網(wǎng)絡N個輸入層神經(jīng)元,；M個決策樹葉節(jié)點對應神經(jīng)網(wǎng)絡M個隱層神經(jīng)元；D種決策樹分類策略對應D個輸出層神經(jīng)元,；L個決策樹內(nèi)部連接對應L個神經(jīng)元連接,；決策樹連接權重W對應神經(jīng)元間連接權重W。
由于DTBNN中隱層神經(jīng)元個數(shù)是通過決策樹的葉節(jié)點決定的,，所以導致構建的隱層神經(jīng)元復雜并且容易出現(xiàn)神經(jīng)網(wǎng)絡過擬合現(xiàn)象,。因此劉棟等人通過對信息熵最大增益原理的研究，提出DTBNN中隱層神經(jīng)元的個數(shù)可以由決策樹的深度決定［9］,。即在一棵決策樹中,，存在一條從根節(jié)點到葉節(jié)點間的最長合取鏈，該鏈的長度為樹的深度,。當神經(jīng)網(wǎng)絡中隱層神經(jīng)元的數(shù)目取決策樹最大合取鏈長度時,，網(wǎng)絡效果最佳，同時既不會出現(xiàn)不正確的分類,，也不會出現(xiàn)過擬合的現(xiàn)象,。劉棟通過“異或問題”和“醫(yī)學分類問題”兩個實驗分別驗證了此改進算法的有效性。
根據(jù)參考文獻［8］,、［9］所提出的基于決策樹的神經(jīng)網(wǎng)絡構建方法,，本文對DTBNN構建方法進行適當改進之后，應用在圖像閾值分割的神經(jīng)網(wǎng)絡構建過程中,。提出決策樹與神經(jīng)網(wǎng)絡之間的對應規(guī)則：（1）決策樹的分支條件數(shù)對應神經(jīng)網(wǎng)絡輸入層神經(jīng)元個數(shù),；（2）決策樹的深度對應神經(jīng)網(wǎng)絡隱層神經(jīng)元個數(shù)；（3）決策樹的分類數(shù)對應神經(jīng)網(wǎng)絡的輸出層神經(jīng)元個數(shù),；（4）決策樹中的連接對應神經(jīng)元間的連接,。
2基于DTBNN的雙閾值圖像分割
2.1雙閾值圖像分割
設大小為X×Y的數(shù)據(jù)圖像，其灰度值f(x, y)取0, 1, 2, … ,L-1, L表示圖像的灰度級,，本文取256,。令Di={(x,y):f(x,y)=i,(x,y)∈D},hi=ni/N，其中D為圖像像素全體集合域,，i=0, 1, … , L-1為灰度值,，Di表示圖像中屬于灰度i的像素集合，ni表示Di中圖像像素的個數(shù),，N=X×Y為總像素個數(shù),，hi為灰度i的概率分布。則H={h0, h1, … , hL-1}表示圖像的灰度直方圖。
本文采用雙閾值分割圖像,，利用閾值門限t1和t2將圖像域D分割為Dl,、Dt、Dm三個域,。其中Dl為非目標域,，灰度級低的部分；Dt為目標域,，灰度符合閾值范圍的部分,；Dm為非目標域，灰度級高的部分,。即Dl={(x,y):f(x,y)≤t1,(x,y)∈D},，Dt={(x,y):t1<f(x,y)≤t2,(x,y)∈D},，Dm={(x,y):t2<f(x,y),(x,y)∈D},。則其灰度的概率分布有：
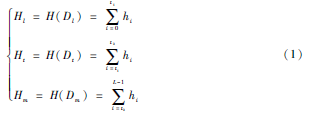
另外，從圖像灰度直方圖中可以得到兩個基本特征信息：灰度均值和最大灰度偏移,，分別用M和S表示,。灰度均值M是圖像中所有灰度級與其概率分布的乘積和,，在灰度直方圖中表現(xiàn)為圖像整體灰度趨向性,，其值越小表明圖像整體偏暗，反之則偏亮,。最大灰度偏移S是圖像中存在的任意灰度級與灰度均值M差的最大值,，在灰度直方圖中表現(xiàn)為峰值(或谷值)與灰度均值的差，其值反映明暗變化度,。計算公式如式(2)所示,。
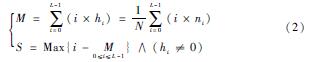
因為M和S分別表征了圖像中的灰度趨向性和相對變化差，則對于工程中要分割的灰度圖像存在函數(shù)映射關系T=G(m, s),，其中T為閾值t1和t2構成的一維向量且有t1<t2,，G(m, s)為對應映射關系集，m為被測圖像的灰度均值并且m∈［0,255］,，s為被測圖像的最大灰度偏移并且s∈［0,255),。其映射關系集G如式(3)。
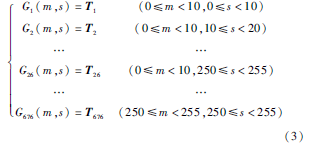
其中,，m和s以10為梯度分別劃分為26個范圍域,，則m和s的組合分類數(shù)為676，Gi1≤i≤676(m,s)表示在i分類下對應的映射關系函數(shù),，Ti表示在i分類下的閾值向量,。
2.2構建DTBNN
在參考文獻［8］、［9］所研究的DTBNN算法基礎上，本文提出建立在雙閾值圖像的DTBNN構建方法,。本文設計的 DTBNN構建步驟如下：
?。?)根據(jù)決策樹與神經(jīng)網(wǎng)絡對應規(guī)則，確定神經(jīng)網(wǎng)絡的層數(shù),、輸入和輸出神經(jīng)元數(shù),；
（2)以最大合取鏈確定神經(jīng)網(wǎng)絡的隱層神經(jīng)元數(shù),；
?。?)按照規(guī)則設置網(wǎng)絡參數(shù)初始值；
?。?)為神經(jīng)網(wǎng)絡中各神經(jīng)元添加連接,；
（5)對神經(jīng)網(wǎng)絡進行訓練,。
由式(3)可知,，圖像灰度均值m和圖像最大灰度偏移s與分割閾值映射函數(shù)G之間形成對應分類關系。由這種分類關系可以生成一棵多分支的分類決策樹,，邏輯示意如圖2,， mi為第i類的灰度均值范圍域，si為第i類的最大灰度偏移范圍域,，Gi為i類的映射關系函數(shù),。圓形節(jié)點為決策樹的內(nèi)部判定節(jié)點，m和s在各自范圍域內(nèi)構成判定分支,，方形節(jié)點為決策樹的分類信息,。根據(jù)工程中圖像特點，將滿足{Gi(m,s):50≤m<200,20≤s<150}條件的分支保留,，將其余分支剪去,，以減小分類決策樹的冗余度。
圖2分類決策樹邏輯結構由圖2所示的分類決策樹,，經(jīng)過剪枝算法和映射關系合并,，最終生成低冗余分類決策樹。按照決策樹與神經(jīng)網(wǎng)絡的對應規(guī)則,，將神經(jīng)網(wǎng)絡設計為輸入層,、隱層和輸出層。輸入層神經(jīng)元數(shù)等于決策樹中的判定參數(shù),，在本文中為26個,；輸出層神經(jīng)元數(shù)等于分類決策樹的分類數(shù)，在本文中經(jīng)過合并與剪枝后為6個,；隱層神經(jīng)元數(shù)為最大合取鏈長度即為決策樹的深度,，在本文中為10個。本文構建的神經(jīng)網(wǎng)絡邏輯示意圖如圖3所示，其中Wi為輸入層神經(jīng)元到隱層神經(jīng)元之間的連接權,，Wo為隱層神經(jīng)元到輸出層神經(jīng)元之間的連接權,，m為被測圖像的灰度均值作為輸入?yún)?shù)，s為被測圖像最大灰度偏移作為輸入?yún)?shù),，t1和t2為圖像分割所需的上下門限值,。
輸入層到隱層的連接權Wi為26×10的矩陣，設基礎權值為ωi,，Wi矩陣中被剪枝掉的連接其權值均為-ωi, 其余連接的權值為ωi,。隱層到輸出層的連接權Wo為10×6的矩陣，設基礎權值為ωo,，Wo矩陣中所有連接的權值均為ωo,。根據(jù)李愛軍等人對兩層權值的初始設置規(guī)則證明［8］，此方法比將兩個連接權矩陣初始化為隨機權值具有更好的網(wǎng)絡學習效果和收斂性,，在本文中將基礎權值ωi和ωo設置為ωi=ωo=0.4,。將帶有連接權值的連接加入到各層神經(jīng)元之間，使其由獨立的分層結構組成帶權連接網(wǎng)絡,，形成初始神經(jīng)網(wǎng)絡,。
建成初始神經(jīng)網(wǎng)絡后,，對采樣的圖像數(shù)據(jù)分別提取出圖像灰度均值,、圖像最大灰度偏差以及對應的映射關系記錄(總共343條)作為訓練集和測試集的樣本空間。從樣本空間中抽出300條記錄作為訓練集,，40條記錄作為測試集,。并將神經(jīng)網(wǎng)絡的學習率設為0.5，動量因子設為0.01,。將初始網(wǎng)絡用訓練集進行訓練后成為最終的神經(jīng)網(wǎng)絡,，其表現(xiàn)出良好的閾值函數(shù)篩選效果。
3實驗數(shù)據(jù)分析
圖4為實際工程中用Manta G201B型CCD工業(yè)攝像機采集的原始圖像,，要求基于機器視覺方式測量出手輪下方六角形螺母旋轉角度,。將求解旋轉角度問題轉化為識別出六角形螺母的一個有效側棱面。由于問題中被測物在不同旋轉角度的情況下,，被測物對外界照明光線反射形成的圖像存在動態(tài)不定性,，本文采用基于DTBNN算法的雙閾值圖像分割方法，并通過MATLAB仿真將本文方法與Otsu雙閾值法,、最大熵雙閾值法進行比較,。
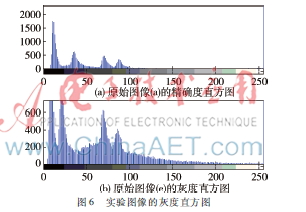
首先采用劃定區(qū)域切割法將被測六角形螺母從原始整體圖像中分離出來，其分離后的圖像如圖5(a)和(e)所示,。然后分別采用本文所提出的方法,、Otsu雙閾值方法和雙閾值最大熵方法進行雙閾值圖像分割，其閾值分割結果如圖5所示。圖5(a)和(e)的灰度直方圖如圖6所示,。
對圖5(a)和圖5(e)使用Otsu雙閾值方法獲取的灰度閾值上下限分別為203,、206和246、249,，能將圖5(a)中六角形螺母清晰分割出來,，如圖5(b)，而圖5(e)不能分割出來,，如圖5(f),。使用最大熵雙閾值法對圖5(a)和圖5(e)進行閾值分割得到分割灰度閾值上下限分別為110、241和71,、114,，能將圖5(a)的六角形螺母的邊緣輪廓分割出來，如圖5(c),，而不能將圖5(e)分割出來,，如圖5(g)。采用本文提出的DTBNN雙閾值方法對圖5(a)和圖5(e)進行閾值分割,，獲取的分割灰度閾值上下限為1,、35和1、25,，此方法將六角形螺母左側棱面清晰分割出來,，如圖5(d)和圖5(h)。在圖5(a)的情況下,，根據(jù)其對應的灰度直方圖圖6(a)可知其灰度直方圖存在明顯峰值特征,，因此以上三種方法都能夠?qū)D5(a)進行有效的雙閾值圖像分割。而圖5(e)沒有明顯的灰度峰值特征,，因此Otsu雙閾值方法和最大熵雙閾值方法都不能有效分割出圖像,。
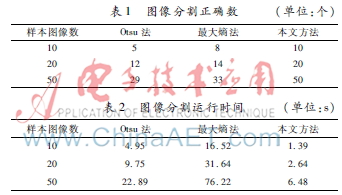
另外，從實驗采集的343個樣本圖像中分別隨機地提取三組測試圖像數(shù)據(jù),，每組分別包含10,、20、50個樣本圖像,。對所抽取的測試圖像組分別采用Otsu雙閾值,、最大熵雙閾值和本文所提出的方法進行圖像分割，其統(tǒng)計如表1和表2所示,。Otsu雙閾值分割法和最大熵雙閾值分割法在處理工程實驗圖像數(shù)據(jù)時,，其正確分割概率分別為56%和72%。而對于本文所提出的方法,，不論被測圖像灰度直方圖是否存在峰值特征,，都能使用經(jīng)過訓練后的網(wǎng)絡計算出閾值并將被測圖像的六角形螺母側棱面正確分割出來,，其正確率接近100%。同時從表2統(tǒng)計結果分析,，Otsu雙閾值分割方法平均運行耗時為0.48 s,，最大熵雙閾值分割方法平均運行耗時為1.59 s。而對于本文提出的DTBNN方法運行時間比Otsu雙閾值和最大熵雙閾值方法都要少,，其平均運行耗時為0.13 s,。表明本文所提出的雙閾值圖像分割方法比Otsu雙閾值方法、最大熵雙閾值方法在圖像雙閾值分割上有更好的運行效率,，能夠適應動態(tài)圖像的圖像分割,。
4結論
將基于決策樹的神經(jīng)網(wǎng)絡分類算法應用于圖像閾值分割領域，通過實驗驗證其分類決策算法能夠使動態(tài)圖像獲取合適的雙閾值圖像分割門限,，并在實際工程中應用該方法達到了解決實際問題的目的,。實驗表明，對于動態(tài)圖像其灰度直方圖有無明顯特征信息都不會對此方法造成影響,，并且因該方法基于分類決策樹構建神經(jīng)網(wǎng)絡,，使得采用較少的訓練樣本就能夠得到穩(wěn)定的神經(jīng)網(wǎng)絡。
另外,，本課題由“北方工業(yè)大學優(yōu)勢學科項目”和“北京市屬高等學校創(chuàng)新團隊建設與教師職業(yè)發(fā)展計劃項目”支持,。
參考文獻
［1］ 丁銳, 劉甲甲, 李柏林, 等. 改進的Otsu圖像多閾值分割方法［J］.計算機應用, 2013, 33(S1):214217.
?。?］ 童小念, 施博, 王江晴. 基于量子粒子群算法的雙閾值圖像分割方法［J］.四川大學學報(工程科學版), 2010, 42(3): 132138.
?。?］ 張春麗. 基于分層遺傳算法的雙閾值圖像分割［J］.微計算機應用, 2008, 29(1):9295.
［4］ 陶文兵, 劉李漫, 田金文, 等. 采用遺傳算法與最大模糊熵的雙閾值圖像分割［J］.信號處理, 2005, 21(6):684687.
?。?］ 周鮮成, 申群太, 王俊年. 基于最大模糊熵和微粒群的雙閾值圖像分割［J］.計算機工程與設計, 2008, 29(12):31883190.
?。?］ 劉欣欣, 李雪, 王瓊. 基于灰度直方圖的多閾值分割法［J］.計算機應用與軟件， 2013, 30(12): 2830.
?。?］ SETHI I K. Neural implementation of tree classifier［J］.IEEE Transactions on Systems, Man & Cybernetics, 1995, 25(8):12431249.
［8］ 李愛軍, 羅四維, 黃華, 等. 基于決策樹的神經(jīng)網(wǎng)絡［J］.計算機研究與發(fā)展, 2005, 42(8): 13121317.
?。?］ 劉棟, 馮勇, 趙向輝. 基于決策樹算法確定一個最小神經(jīng)網(wǎng)絡［J］.計算機應用, 2010, 30(Z1): 8385.