張兢,李冠迪,史文進(jìn),曾建梅
(重慶理工大學(xué) 電子信息與自動(dòng)化學(xué)院,重慶 400054)
摘要:分析了小波去噪的特點(diǎn),針對(duì)軟、硬閾值的缺陷,構(gòu)造出一種新的閾值函數(shù)及閾值估計(jì)方法。新閾值函數(shù)連續(xù)可導(dǎo)并且新閾值估計(jì)方法具有優(yōu)良的自適應(yīng)性。仿真實(shí)驗(yàn)表明,該方法可以有效去除白噪聲干擾,信噪比更高,均方根誤差更小,且重構(gòu)信號(hào)的近似性好。
關(guān)鍵詞:小波閾值去噪;閾值函數(shù);閾值估計(jì);信噪比;均方根誤差
0引言
在信號(hào)的采集、傳輸過(guò)程中,不可避免地會(huì)受到各種噪聲干擾,對(duì)信號(hào)去噪處理已成為人們關(guān)注和研究的熱點(diǎn)。小波變換具有多分辨率分析的特點(diǎn),在時(shí)域和頻域都有表征信號(hào)局部信息的能力[1],時(shí)間窗和頻率窗都可以根據(jù)信號(hào)的具體形態(tài)動(dòng)態(tài)調(diào)整,能有效區(qū)分非平穩(wěn)信號(hào)中的突變部分和噪聲[2],可在提高信噪比的同時(shí)保持對(duì)突變信息的良好分辨能力。
小波去噪方法有:模極大值法、小波閾值去噪法以及相關(guān)去噪法。其中,運(yùn)用最為廣泛的是DONOHO D L在1995年提出的小波閾值去噪的算法[3-4],該方法處理含噪信號(hào)時(shí)采用軟閾值函數(shù)與硬閾值函數(shù)。但傳統(tǒng)軟閾值函數(shù)存在恒定偏差缺陷,以及硬閾值函數(shù)有振蕩現(xiàn)象的缺陷[5]。本文深入分析小波軟硬閾值的優(yōu)缺點(diǎn),綜合其他學(xué)者提出的閾值函數(shù),在此基礎(chǔ)上構(gòu)造出一種新的閾值估計(jì)與閾值函數(shù)。通過(guò)仿真實(shí)驗(yàn)分析,新閾值函數(shù)連續(xù)可導(dǎo),既解決了軟閾值函數(shù)存在恒定偏差的問(wèn)題,又解決了硬閾值函數(shù)存在振蕩現(xiàn)象的問(wèn)題,具有較好的實(shí)用性。
1小波閾值去噪基本原理
1.1小波變換
假設(shè)含噪信號(hào)的觀測(cè)值為f(t),則:

其中,s(t)為信號(hào)在時(shí)刻t的真實(shí)值,n(t)為高斯白噪聲,σ為噪聲標(biāo)準(zhǔn)差。小波變換的目的是抑制n(t)以恢復(fù)s(t)。對(duì)于一維信號(hào)f(t)而言,首先要對(duì)它進(jìn)行離散采樣,得到N點(diǎn)離散信號(hào)f(n),n=1,2,…,N-1,其小波變換為:

ωf(j,k)為小波系數(shù)記為ωj,k。由于小波變換屬于線性變換,因此對(duì)含噪信號(hào)f(t)=s(t)+σn(t)作離散變換后,得到的小波系數(shù)j,k仍舊是由真實(shí)信號(hào)s(t)對(duì)應(yīng)的小波系數(shù)和噪聲信號(hào)n(t)所對(duì)應(yīng)的小波系數(shù)兩部分組成。
1.2小波閾值去噪
從數(shù)學(xué)角度分析,小波閾值去噪本質(zhì)上是函數(shù)逼近問(wèn)題;從信號(hào)處理角度分析,則為信號(hào)濾波問(wèn)題[6]。在實(shí)際信號(hào)中,噪聲通常分布在高頻信號(hào)中,而純凈信號(hào)通常分布在低頻信號(hào)中,則可通過(guò)設(shè)置閾值方法將噪聲信號(hào)分離出去[7]。小波閾值去噪法的流程圖如圖1所示。

其中,f(x)為含噪信號(hào),f^(x)為重構(gòu)信號(hào)。由以上流程圖可得閾值函數(shù)和閾值的選取直接影響到最終的去噪效果,閾值選取過(guò)小,則會(huì)消噪不足,致使信號(hào)的弱特征成份被噪聲淹沒(méi);反之,則會(huì)導(dǎo)致“過(guò)扼殺”的現(xiàn)象。
設(shè)ωj,k為原始小波系數(shù),ω^j,k為閾值處理后的小波系數(shù),λ=σ2log(N)為統(tǒng)一閾值,則λ>0,傳統(tǒng)閾值去噪有:
(1)硬閾值(Hard Thresholding)
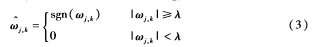
(2)軟閾值(Soft Thresholding)

為了對(duì)比軟閾值與硬閾值的處理效果,設(shè)一原始信號(hào)為:
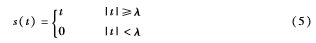
分別對(duì)其進(jìn)行軟閾值和硬閾值去噪,仿真結(jié)果如圖2所示。

由圖2可知,硬閾值函數(shù)在ωj,k=±λ處不連續(xù),去噪時(shí)造成較大方差,重構(gòu)信號(hào)出現(xiàn)偽吉布斯現(xiàn)象。軟閾值函數(shù)的小波系數(shù)連續(xù)性雖好,但當(dāng)ωj,k>λ或ωj,k<-λ時(shí),軟閾值對(duì)小波系數(shù)進(jìn)行壓縮時(shí)存在恒定的偏差,并且軟硬閾值函數(shù)不具有高階可導(dǎo)性,不易實(shí)現(xiàn)數(shù)字處理。因此,尋找一種既可以克服軟硬閾值缺陷,又高階可導(dǎo)的新閾值函數(shù)至關(guān)重要。
2新閾值函數(shù)與閾值估計(jì)
2.1閾值函數(shù)的選取
針對(duì)上述軟閾值與硬閾值的不足,學(xué)者們提出了許多改進(jìn)閾值函數(shù),較經(jīng)典的如參考文獻(xiàn)[8]提出的一種自適應(yīng)的閾值函數(shù):
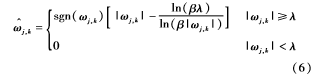
上述的閾值函數(shù)具有很好的自適應(yīng)性,但是卻存在振蕩和偽吉布斯效應(yīng),在閾值處并不光滑。為了克服這些弱點(diǎn)本文在此基礎(chǔ)之上構(gòu)造了一種新的閾值函數(shù):

其中,α為調(diào)節(jié)參數(shù),由式(7)可以看出,當(dāng)α→0時(shí)為軟閾值函數(shù),當(dāng)α→∞時(shí)為硬閾值函數(shù)。由此可見(jiàn),構(gòu)造的新閾值函數(shù)同時(shí)具有軟閾值函數(shù)與硬閾值函數(shù)特點(diǎn),靈活性較好。因此根據(jù)不同的去噪目的去調(diào)節(jié)α值,可得到較好的去噪效果。并且當(dāng)ωj,k→±λ時(shí),j,k→0,j,k在ωj,k=±λ處是連續(xù)的,即與硬閾值函數(shù)相比,重構(gòu)信號(hào)不會(huì)產(chǎn)生震蕩。
構(gòu)造的新閾值函數(shù)不但具有連續(xù)性,并且當(dāng)ωj,k>λ或ωj,k<-λ時(shí)具有高階可導(dǎo)性,新閾值函數(shù)對(duì)各種數(shù)字信號(hào)處理都很方便,證明如下:
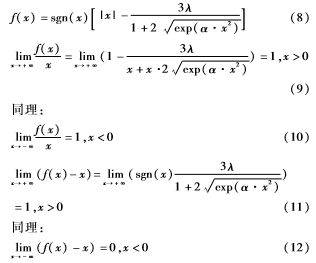
由式(8)~(12)可知,f(x)以y=x作為漸近線,同理可得本文采用的改進(jìn)的閾值函數(shù)以j,k=ωj,k為漸近線,并且ωj,k值越大,小波系數(shù)估計(jì)值j,k越接近ωj,k,進(jìn)而克服硬閾值的小波系數(shù)不連續(xù),以及軟閾值函數(shù)的j,k與ωj,k存在恒定偏差的缺陷。
2.2改進(jìn)閾值估計(jì)
在小波閾值去噪中不僅閾值函數(shù)是影響去噪效果的關(guān)鍵因素,閾值估計(jì)也至關(guān)重要。目前,人們通常采用統(tǒng)一閾值,但是此閾值與信號(hào)長(zhǎng)度N相關(guān),信號(hào)長(zhǎng)度N越大,小波系數(shù)被置0的數(shù)目越多,導(dǎo)致“過(guò)扼殺”現(xiàn)象[9];反之則會(huì)導(dǎo)致消噪不足的現(xiàn)象。為了避免上述現(xiàn)象發(fā)生,在統(tǒng)一閾值的基礎(chǔ)上引入了一個(gè)適中的收縮因子,新閾值估計(jì)的數(shù)學(xué)公式為:
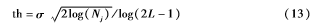
式中,σ為噪聲標(biāo)準(zhǔn)差,Nj為各層高頻系數(shù)的長(zhǎng)度,L為分解層數(shù)。由式(13)可得:隨著分解層數(shù)L的不同,閾值估計(jì)的大小隨之自動(dòng)調(diào)節(jié),因此具有較強(qiáng)的自適應(yīng)性。
3仿真實(shí)驗(yàn)及分析
3.1去噪效果的評(píng)價(jià)指標(biāo)
采用信噪比SNR和均方根誤差RMSE對(duì)去噪效果進(jìn)行比較評(píng)價(jià),信噪比表示的是信號(hào)中含有噪聲的多少,其值越大,信號(hào)中噪聲含量越少;均方根誤差表示測(cè)量樣本的可靠性,其值越小,測(cè)量的可靠性越高。表達(dá)式如式(14)和式(15)所示。
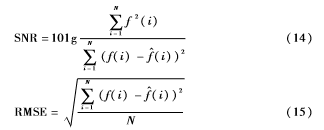
其中,f(i)為原始不含噪信號(hào),f^(i)為去噪后的信號(hào),N為信號(hào)長(zhǎng)度。
3.2實(shí)驗(yàn)結(jié)果分析
為了驗(yàn)證新閾值函數(shù)的有效性,用MATLAB2010對(duì)其進(jìn)行仿真,將一段含有噪聲的Leleccum信號(hào)分別采用硬閾值、軟閾值、參考文獻(xiàn)[8]提出的閾值函數(shù)及本文構(gòu)造的新閾值函數(shù)進(jìn)行去噪實(shí)驗(yàn)。經(jīng)多次試驗(yàn)可得,選取sym4小波分解5層,且調(diào)節(jié)參數(shù)α取值為5×10-5時(shí)得到的效果最好。所以本實(shí)驗(yàn)選取sym4小波及5層小波分解進(jìn)行實(shí)驗(yàn)。實(shí)驗(yàn)中含噪Leleccum信號(hào)的信噪比為26.199 6 dB,調(diào)節(jié)參數(shù)α=5×10-5,進(jìn)行仿真實(shí)驗(yàn),測(cè)試結(jié)果如圖3所示。

從圖3可以看出,本文提出的改進(jìn)閾值函數(shù)小波重構(gòu)得到的信噪比硬閾值函數(shù)以及參考文獻(xiàn)[8]提出方法重構(gòu)信號(hào)更平滑,比軟閾值函數(shù)重構(gòu)信號(hào)保留的有用信號(hào)更多,因而能更好地還原原始信號(hào)所包含的信息。
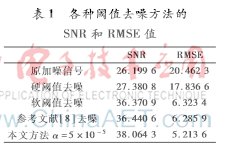
表1給出了4種閾值函數(shù)去噪后的信噪比和均方誤差。從實(shí)驗(yàn)結(jié)果數(shù)據(jù)可以看出,本文提出的閾值方法相比軟、硬閾值方法以及參考文獻(xiàn)[8]方法,在信噪比和均方根誤差兩個(gè)性能指標(biāo)上均有明顯的提高,說(shuō)明改進(jìn)后的方法可靠性更強(qiáng),去噪效果更好。
4結(jié)論
本文構(gòu)造出了新閾值函數(shù)和閾值估計(jì)方法,新閾值函數(shù)具有軟硬閾值優(yōu)點(diǎn),同時(shí)具有連續(xù)可導(dǎo)性,并且通過(guò)自適應(yīng)調(diào)整參數(shù)α消除了軟閾值函數(shù)的恒定偏差、硬閾值函數(shù)不連續(xù)以及引用參考文獻(xiàn)提出的閾值函數(shù)光滑性差的缺點(diǎn)。改進(jìn)的閾值估計(jì)隨分解尺度的變化自適應(yīng)調(diào)節(jié)閾值的大小,避免了“過(guò)扼殺”現(xiàn)象的產(chǎn)生。仿真結(jié)果表明,新閾值去噪方法重構(gòu)得到的信號(hào)質(zhì)量明顯優(yōu)于軟閾值方法、硬閾值方法以及參考文獻(xiàn)[8]提出的方法,在去除噪聲的同時(shí)很好地保留了有用信號(hào),證明了算法的有效性與實(shí)用性。
參考文獻(xiàn)
[1] 劉征.雷達(dá)輻射源信號(hào)的時(shí)頻分析方法研究[D].太原:中北大學(xué),2011.
[2] 王旭.小波閾值去噪法在建筑物變形監(jiān)測(cè)數(shù)據(jù)處理中的應(yīng)用研究[D].阜新:遼寧工程技術(shù)大學(xué),2011.
[3] DONOHO D L, JOHNSTONE I M.Ideal spatial adaptation via wavelet shrinkage[J].Biometrika,1994,81(12):425 455.
[4] DONOHO D L.Denoising by softtresholding[J].IEEE Transactions on Information Theory,1995,41(3):613 627.
[5] 張弛,李翔,姚磊.一種改進(jìn)的小波閾值函數(shù)去噪方法[J]. 計(jì)算機(jī)與現(xiàn)代化,2014,40(3):219 222.
[6] 景新幸,冼燦嬌,楊海燕.基于改進(jìn)的小波閾值去噪算法的研究[J].電聲技術(shù),2015,39(5):80 83.
[7] MALLAT S G. Theory for multiresolution signal decomposition:the wavelet representation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1989,11(7):674 693.
[8] 夏欣,李海標(biāo),沈蘭蘭,等.一種改進(jìn)的小波閾值裂紋圖像去噪法[J]. 電子設(shè)計(jì)工程,2013,21(18):130 132.
[9] 王琪,程彬,杜娟,等.一種改進(jìn)的小波閾值圖像去噪方法[J].計(jì)算機(jī)與現(xiàn)代化,2015(4):65 69.

