0 引言

　　實際的工程測量測試中，工程信號在采集和傳輸過程中,，總會因外界的干擾引入噪聲,，為了準(zhǔn)確地獲得有用信號，降噪是信號分析前必須經(jīng)過的預(yù)處理環(huán)節(jié),。傳統(tǒng)降噪方法的不足在于使信號變換后的熵增高,，無法刻畫信號的非平穩(wěn)特性并且無法得到信號的相關(guān)性[1]。而小波變換在時域和頻域同時具有良好的局部化性質(zhì),，并且小波變換具有眾多優(yōu)良的特性,，如多分辨率特性、低熵性,、去相關(guān)性和選基靈活性等,。這些特性很好地克服了傳統(tǒng)方法的不足，使得小波變換適用于信號的降噪處理,。因此利用小波變換進(jìn)行降噪,，已經(jīng)成為近幾年研究的熱點。

　　運用小波變換處理噪聲的方法主要分為3類：MATLAB提出的模極大值處理算法[2],；XU提出的空域相關(guān)降噪算法[3],；DONOHO提出的閾值降噪算法[4]。其中,，以閾值降噪算法最為常用,。閾值降噪算法中，通過對分解后的小波系數(shù)進(jìn)行閾值處理以達(dá)到降噪的目的,。最常用的閾值函數(shù)是由DONOHO在1995年提出的硬閾值函數(shù)和軟閾值函數(shù),，但這兩種函數(shù)也存在不足之處。采用硬閾值函數(shù)時,，由于硬閾值函數(shù)的不連續(xù),，導(dǎo)致重構(gòu)信號可能出現(xiàn)局部震蕩,；采用軟閾值函數(shù)時，與真實小波系數(shù)之間存在恒定的偏差,，導(dǎo)致重構(gòu)后信號的精度下降[5],。針對軟、硬閾值函數(shù)存在的缺點和不足,，本文提出一種新的閾值函數(shù),。新閾值函數(shù)既保證了閾值函數(shù)的連續(xù)性，又能避免軟閾值固定偏差的缺點,。并通過MATLAB仿真分析驗證了改進(jìn)的小波閾值降噪算法優(yōu)于傳統(tǒng)閾值算法,。

1 小波閾值降噪原理

　　假設(shè)一維離散含噪信號由式(1)表示：

　　其中，X(k)是含噪信號,；S(k)是原始標(biāo)準(zhǔn)信號,；E(k)是疊加的高斯白噪聲，其服從N(0,，σ2)分布,。

　　小波變換后，有用信號的能量集中于幅值較大的小波系數(shù),，而噪聲能量則分布在整個小波域中[6],。因此，較大的小波系數(shù)是由有用信號引起的,，較小的小波系數(shù)則代表噪聲,。基于小波系數(shù)的特征,，DONOHO和JOHNSTONE[7]提出了閾值降噪算法,。首先確定一個閾值，即選擇一個合適的數(shù),，當(dāng)小波分解系數(shù)小于閾值時,，認(rèn)為這部分系數(shù)主要是由噪聲引起的，予以舍棄,；當(dāng)系數(shù)大于閾值時,，認(rèn)為這是由信號引起的小波分解系數(shù),，就把這一部分進(jìn)行閾值處理,，然后用閾值處理后的量化系數(shù)進(jìn)行重構(gòu)，即為降噪后的信號,。小波閾值降噪的基本步驟如圖1所示,。

2 改進(jìn)閾值算法

　　閾值的確定直接影響著小波閾值降噪的效果。如果閾值取得太小,，噪聲依然存在,；如果閾值取得太大,，那么有用信號的重要信息也可能被濾除。最常選用的通用閾值可用式(2)表示：

　　其中,，N為信號的長度,，σ為噪聲的均方差估計值，由式(3)給出：

　　因為通用閾值有過扼殺有用信號的風(fēng)險,，文獻(xiàn)[6]提出一種基于層間相關(guān)性的閾值選取方法,。本文在此基礎(chǔ)上結(jié)合分層閾值的思想對該閾值算法進(jìn)行改進(jìn)，如式(4)所示：

　　其中,，r為常數(shù),，Tj，n為小波分解第j層位置n處的閾值,，λj為第j層的閾值,，其表達(dá)式如式(5)所示：

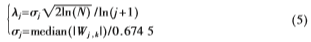
　　式中，Wj,，k為第j層上的小波系數(shù),，j為分解層數(shù)。

　　K(n)為定義的一個參數(shù),，用來表征小波系數(shù)的層間相關(guān)性,，其定義如式(6)所示：

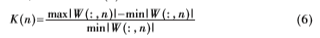
　　式中，W(:,，n)表示點n處的所有小波系數(shù),。

　　當(dāng)K(n)∈[0，r),，點n處的小波系數(shù)相關(guān)性較強,，點n處可能是一個信號點；當(dāng)K(n)∈[r,，+∞),，點n處的相關(guān)性較差，該點可能是由噪聲引起的,。由式(4)可知,，新閾值方法通過比較小波系數(shù)層間相關(guān)性，對不同點n的閾值進(jìn)行修正,。當(dāng)K(n)∈[0,，0.5r)時，小波系數(shù)間的相關(guān)性很大,，該點非常有可能是純信號點,，對閾值進(jìn)行收縮，取為0.7λj,；當(dāng)K(n)∈[0.5r,，0.8r)時,，小波系數(shù)的相關(guān)性比較大，該點有可能是信號點,，該點的閾值取為0.8λj,；當(dāng)K(n)∈[0.8r，r)時,，相關(guān)性較大,，該點依舊可能是信號點，減小閾值收縮程度,，取為0.9λj,；當(dāng)K(n)∈[r，+∞)時,，認(rèn)為小波系數(shù)的相關(guān)性較小,，該點幾乎不可能是純信號點，將閾值取為λj,。

　　K(n)在計算時,，要求不同層上的小波分解系數(shù)的數(shù)目一致，因此需要采用平穩(wěn)小波變換(SWT),。r是測量小波系數(shù)相關(guān)性的一個重要參數(shù),，取值太小，可能會過扼殺有用信號,，取值過大,，可能會保留較多的噪聲信息。通過相關(guān)實驗,，r取為0.5~1.5之間時,，降噪效果比較好。本文中,，r取為1,。

3 構(gòu)造新閾值函數(shù)

　　傳統(tǒng)的閾值函數(shù)是由DONOHO提出的軟閾值函數(shù)和硬閾值函數(shù)，軟閾值函數(shù)定義如式(7)所示,，硬閾值函數(shù)定義如式(8)所示,。

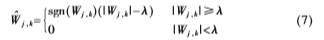
　　硬閾值函數(shù)在小波域內(nèi)存在間斷點，在重構(gòu)信號時會出現(xiàn)局部震蕩現(xiàn)象,；軟閾值函數(shù)雖然在小波域內(nèi)連續(xù),，但是閾值處理后的小波系數(shù)與真實小波系數(shù)存在恒定偏差，會造成信號高頻有用信息的丟失,。

　　本文結(jié)合文獻(xiàn)[8]與文獻(xiàn)[9]中的方法,，構(gòu)造了一個新的閾值函數(shù),，如式(9)所示：

　　其中,，且α為正數(shù),，β為正數(shù)。

　　由式(9)可知,，當(dāng)|Wj,，k|→±λ時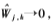，,，即新閾值函數(shù)在Wj,，k=±λ處是連續(xù)的，克服了硬閾值函數(shù)不連續(xù)的缺陷,，重構(gòu)信號不會有震蕩產(chǎn)生,；當(dāng)Wj，k→±∞時,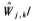，,，即當(dāng)小波系數(shù)足夠大時，新閾值函數(shù)等同于硬閾值函數(shù),，從而克服了軟閾值函數(shù)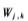之間具有恒定偏的問題,；同時新閾值函數(shù)具有高階可導(dǎo)性。從表達(dá)式中可以看出,，當(dāng)α→0且β→0時,，新閾值函數(shù)即為軟閾值函數(shù)；當(dāng)α→+∞時,，u→1,，新閾值函數(shù)即為硬閾值函數(shù)；適當(dāng)選取α和β的值,，新閾值函數(shù)可以在硬閾值函數(shù)與軟閾值函數(shù)之間進(jìn)行調(diào)整,，靈活性更強。硬,、軟閾值函數(shù)的圖形如圖2(a),、圖2(b)所示，選取不同的α和β的新閾值函數(shù)如圖2(c),、圖2(d)所示,。

4 仿真分析

　　為了驗證本文降噪算法的有效性，用MATLAB對其進(jìn)行仿真試驗,。選用Matlab自帶的Heavy sine 信號,，對其加入一定的高斯白噪聲，并用軟閾值降噪算法,、硬閾值降噪算法,、本文新閾值降噪算法分別對其做降噪處理，其結(jié)果如圖3所示。其中,，選用sym4小波基,，分解層數(shù)選為3層，新閾值函數(shù)中將α取為0.1,，β取為7,。

　　從視覺上，降噪效果很難評價,，為了量化地評價降噪性能,，采用信噪比和均方根誤差[10]作為評價指標(biāo)。信噪比指原始信號能量與噪聲能量的比值,，記為SNR,，其值越大，信號中噪聲含量越少,，降噪效果越好,；均方根誤差指重構(gòu)信號與原始信號的均方誤差，記為RMSE,，均方根誤差體現(xiàn)了原始信號和降噪之后的信號間的差異,，均方根誤差越小，表示重構(gòu)信號與原始信號的差異越小,，即降噪效果越好,。其表達(dá)式分別如式(10)和式(11)所示。

　　式中,，x(i)為原始無噪聲信號,；為降噪后的信號。

　　各種降噪方法的性能指標(biāo)如表1所示,。從表中可以看出,，改進(jìn)的閾值降噪算法相比于其他算法，降噪后信噪比最大,，均方根誤差最小,，所以改進(jìn)的閾值降噪算法優(yōu)于其他算法。

5 總結(jié)

　　本文分析了小波閾值降噪的原理,，針對軟,、硬閾值函數(shù)的缺點，結(jié)合相關(guān)文獻(xiàn),，提出了一種新的閾值函數(shù),，該閾值函數(shù)可以通過調(diào)整α和β參數(shù)來調(diào)整閾值函數(shù)，進(jìn)而獲得最佳的降噪效果,。本文基于改進(jìn)的新閾值函數(shù),，并結(jié)合改進(jìn)的閾值確定方法，提出了一種新的閾值降噪算法。利用MATLAB進(jìn)行仿真分析,，實驗結(jié)果表明,，本閾值降噪算法降噪性能優(yōu)于其他常用算法。

　　參考文獻(xiàn)

　　[1] 張德豐.Matlab小波分析[M].北京：機械工業(yè)出版社,，2011.

　　[2] MALLAT S，HWANG W L.Singularity detection and processing with wavelets[J].IEEE Trans Inform Theory,，1992,，38(2)：617-643.

　　[3] XU Y S，WEAVER J B,，HEALY D M,，et al.Wavelet transform domain filters：a spatially selective noise filtration technique[J].IEEE Trans Image Processing，1994,，3(6)：747-758.

　　[4] DONOHO D L.De-noising by soft-thresholding[J].IEEETransactions on Information Theory,，1995，41(3)：613-627.

　　[5] 王立東,，張凱,，王良潤.改進(jìn)小波閾值算法在電機振動信號降噪中的應(yīng)用[J].電子技術(shù)應(yīng)用，2015,，41(5)：77-80.

　　[6] HE C,，XING J C，LI J L,，et al.A new wavelet threshold determination method considering interscale correlation in signal denoising[J].Mathematical Problems in Engineering,，2015.

　　[7] DONOHO D L，JOHNSTONE I M.Ideal spatial adaption by wavelet shrinkage[J].Biometrika,，1994,，81(3)：425-455.

　　[8] 胡俊文，周國榮.小波分析在振動信號降噪中的應(yīng)用[J].機械工程與自動化,，2010,，158(1)：128-130.

　　[9] 王蓓，張根耀,，李智,，等.基于新閾值函數(shù)的小波閾值降噪算法[J].計算機應(yīng)用，2014,，34(5)：1499-1502.

　　[10] 陶珂,，朱建軍.小波去噪質(zhì)量評價方法的對比研究[J].大地測量與地球動力學(xué)，2012,，32(2)：128-133.