0 引言

    在大規(guī)模MIMO系統(tǒng)中,，一個重大的突破是提出了GSM(Generalized Spatial Modulation)和廣義空移鍵控(Generalized Space Shift Keying，GSSK)技術(shù),。GSM調(diào)制比GSSK調(diào)制具有更高的頻譜效率,，但是GSM有更高的檢測復(fù)雜度。在發(fā)射端,，GSSK和GSM只激活小部分的天線,，發(fā)射端的功耗以及射頻鏈的數(shù)量大大減少^[1-3]。本文主要研究GSSK的檢測算法,。

    GSSK中的最大似然(Maximum Likelihood,，ML)算法需要遍歷完所有可能的天線組合，這使得ML的檢測計算復(fù)雜度相當(dāng)高，尤其對于大規(guī)模天線陣列更為明顯,。因此,，一些次優(yōu)的檢測算法被提了出來，例如壓縮感知(Compressive Sensing,，CS)算法^[4-6],。在文獻[4]中，OMP (Orthogonal Matching Pursuit)算法被用于GSSK檢測,，其仿真結(jié)果顯示OMP算法相對于許多傳統(tǒng)的MIMO檢測算法(如MMSE,、ZF算法)有更好的性能以及較低的復(fù)雜度。但是,，隨著信噪比的增加,，它的BER(Bit Error Rate)出現(xiàn)了地板趨勢。在文獻[5]中,，對H矩陣進行SVD(Singular Value Decomposition)預(yù)處理,，其GSSK檢測性能相應(yīng)提高，但檢測復(fù)雜度也相應(yīng)增加,。在文獻[6]中,，在OMP算法基礎(chǔ)上，通過增加迭代次數(shù),，使得GSSK的檢測性能大大提高,，但隨著信噪比的增加，BER也逐漸呈現(xiàn)地板趨勢,。

    本文改進了一個基于CS的GSSK檢測算法,，命名為“ML-OMP-K”。在CS傳統(tǒng)的OMP算法里,，每次迭代僅僅搜索對應(yīng)于稀疏集合的一個位置,，并且當(dāng)殘余量的范數(shù)低于某個閾值或找到的稀疏位置的個數(shù)等于實際的稀疏度時，搜索過程停止,。但當(dāng)接收信號遭受到深衰落時,，在搜索過程中，有時不能找到正確的稀疏位置,。相比OMP算法直接找出AAI(Active Antenna Indices),，在改進的ML-OMP-K算法中，先找出一個小的AAI集合,，稱其為AAI備選集,，再利用ML在該備選集中遍歷搜索，找出AAI,。實際應(yīng)用中,，最終備選集一般較小,，在這個集合內(nèi)進行ML檢測所需的復(fù)雜度較低，同時可以獲得很好的性能,。數(shù)據(jù)結(jié)果顯示,，新算法相比文獻[4-6]中的檢測算法，有更好的檢測性能,，且復(fù)雜度較低,。

1 GSSK系統(tǒng)模型

    假設(shè)大規(guī)模MIMO系統(tǒng)的發(fā)送天線數(shù)為N_t，接收天線數(shù)為N_r,，每一時刻激活天線數(shù)為n_t,，則GSSK系統(tǒng)模型如圖1所示。

    因為GSSK系統(tǒng)是一個大規(guī)模MIMO系統(tǒng),，假設(shè)信道為平坦瑞利衰落信道,，且信道增益在一個符號周期內(nèi)保持不變，則系統(tǒng)模型表達式如下：

2 GSSK檢測算法

    根據(jù)GSSK系統(tǒng)的調(diào)制規(guī)則,，由于x是n_t稀疏的,，故發(fā)送信號矢量x中的大部分位置的元素為0。所以,，在接收端的檢測可以考慮為是一個稀疏重構(gòu)問題,，即可以利用稀疏重構(gòu)理論來檢測出信號x。

    對于稀疏信號,，CS算法有很好的信號恢復(fù)性能,，甚至對于欠定系統(tǒng)也有很好的檢測性能。然而,，CS算法是基于實數(shù)域的，而本系統(tǒng)模型是基于復(fù)數(shù)域的,，因此,，在利用稀疏重構(gòu)之前，需要將式(1)進行變換如下：

    因為l₁范數(shù)問題可以轉(zhuǎn)換成一個等價的線性規(guī)劃問題,，可以通過MP(Matching Pursuit)類算法有效解決,。故已有的OMP算法以及新提出的ML-OMP-K算法均能用于重構(gòu)原始信號，并且當(dāng)GSSK系統(tǒng)滿足條件：N_r=,，x可以以較高的概率被恢復(fù),，其中c為較小的常數(shù)^[8]。

2.1 基于OMP算法的GSSK信號檢測

2.2 基于ML-OMP-K的GSSK信號檢測

    明顯地,，由上述OMP算法可以看出,，每次迭代中，OMP僅選取了一個最大的相關(guān)值對應(yīng)的索引號作為AAI,，但當(dāng)接收信號遭受到深衰落時,，在搜索過程中有時不能找到正確的稀疏位置。因此，在新的算法中作了相應(yīng)的改進,。

    從的每一個集合中選取一個元素進行組合,，將所有組合存于集合B中。

3 性能與復(fù)雜度分析

    為了驗證ML-OMP-K算法的有效性,，本節(jié)將該算法與ML算法和OMP算法進行性能比較,，并分析了算法的復(fù)雜度?？紤]發(fā)射天線數(shù)N_t=128,、激活天線數(shù)n_t=2的GSSK系統(tǒng)，系統(tǒng)的頻譜效率為s=12 bit/s/Hz,。

3.1 性能分析

    本文給出了在不同接收天線N_r=16,、N_r=32下的仿真結(jié)果，并將改進的算法與ML算法和OMP算法進行性能對比,。

    從圖2和圖3中可以看出,，ML-OMP-K的算法性能明顯優(yōu)于OMP算法。圖3中顯示,，在更多接收天線的情況下,，ML-OMP-K算法的性能更加接近于ML，同時OMP算法的性能也相應(yīng)提升,。這是因為,，對于第二部分描述的GSSK信道模型：

    當(dāng)滿足，x可以被較準確地恢復(fù),，其中c為較小的常數(shù),。所以，x的準確恢復(fù)與GSSK系統(tǒng)的接收天線數(shù)密切相關(guān),，在一定范圍內(nèi),，隨著N_r的增加，算法的檢測性能也相應(yīng)提升,。

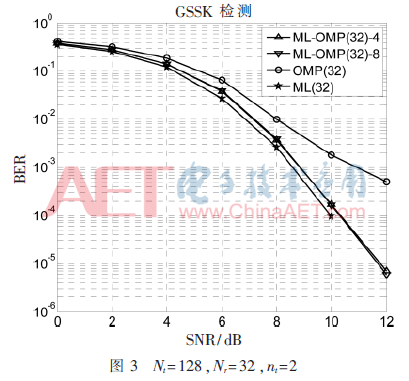
    明顯地,，在N_r=16和N_r=32時，當(dāng)SNR≥10時,，OMP算法逐漸呈現(xiàn)出地板趨勢,。然而，ML-OMP-K算法并沒有呈現(xiàn)出地板趨勢,。相比OMP,，當(dāng)N_r=16，BER=10^-2時,， ML-OMP-K有至少2 dB的性能優(yōu)越,；當(dāng)N_r=32,，BER=10^-3，BER=10^-3.5時,，ML-OMP-K分別有大約2 dB和3 dB的性能優(yōu)越,。同時，當(dāng)K=4與K=8時,，ML-OMP-K算法性能相近,，且非常接近于ML算法的性能。因此,，新的算法對于GSSK信號檢測有明顯的性能提升,。

3.2 復(fù)雜度分析

    用復(fù)乘的操作次數(shù)來定義復(fù)雜度，幾種算法的復(fù)雜度對比如表1所示,。傳統(tǒng)的ML檢測算法等價于尋找H中對應(yīng)激活天線n_t的列,，使下式取最小：

    由表1可得,，當(dāng)N_t=128,，N_r=16，n_t=2,，K=2(或K=4)時,，以及當(dāng)N_t=128，N_r=32,，n_t=2,，K=2(或K=4)時，ML-OMP-K算法的復(fù)雜度約為ML算法的2%,。

4 總結(jié)

    本文改進了一種基于壓縮感知的GSSK信號檢測算法ML-OMP-K,。該算法結(jié)合了ML算法和OMP算法。首先,，在nt次迭代后,，生成一個大小為的AAI候選集。再利用ML算法對該候選集遍歷搜索,，得到對應(yīng)的AAI,。仿真結(jié)果顯示在K=4時,，改進算法的檢測性能接近于ML算法,，且其復(fù)雜度相對于ML算法大大降低。因此,，本文改進的算法有較好的實際應(yīng)用意義,，且利于硬件實現(xiàn)。

參考文獻

[1] WANG J,，JIA S,，SONG J.Generalised spatial modulation system with multiple active transmit antennas and low complexity detection scheme[J].IEEE Trans.Wireless Commun.,，2012，11(4)：1605-1615.

[2] JEGANATHAN J,，GHRAYEB A,，SZCZECINSKI L.Generalized space shift keying modulation for MIMO channels[C].In Proc.IEEE PIMRC，2008：1-5.

[3] PEPPAS K,，ZAMKOTSIAN M,，LAZARAKIS F，et al.Asymptotic error performance analysis of spatial modulation under generalized fading[J].IEEE Wireless Commun.Lett.,，2014,，3(4)：421-424.

[4] YU C M，HSIEH S H,，LIANG H W,，et al.Compressed sensing detector design for space shift keying in MIMO systems[J].IEEE  Commun.Lett.，2012,，16(10)：1556-1559.

[5] WU C H,，CHUNG W H，LIANG H W.OMP-based detector design for space shift keying in large MIMO systems[C].In Proc.IEEE GLOBECOM,，2014：4072-4076.

[6] SREEJITH K,，KALYANI S.Combining ML and compressive sensing：detection schemes for generalized space shift keying[J].IEEE Commun.Lett.，2016,，5(1)：72-75.

[7] CANDES E J,，TAO T.Robust uncertainty principles：exact signal reconstruction from highly incomplete frequency information[J].IEEE Trans.Inf.Theory，2006,，52(2)：489-509.

[8] FOUCART S.Hard thresholding pursuit：an algorithm for compressive sensing[J].SIAM J.Numerical Analysis,，2011，49(6)：2543-2563.