楊義先，鈕心忻
?。ū本┼]電大學(xué) 信息安全中心,， 北京 100876）
0引言
如果說安全的核心是對抗，那么,，在對抗的兩個主角（攻方與守方）中,，攻方（黑客）又是第一主角，因為,，紅客（守方）是因黑客（攻方）而誕生的,。所以，很有必要對黑客，特別是他的攻擊策略,，進(jìn)行更深入的研究,。
廣義地說，系統(tǒng)（或組織）的破壞者,，都統(tǒng)稱為“黑客”,。他（它）們以擾亂既有秩序為目的。因此,，癌細(xì)胞,、病菌、敵對勢力,、災(zāi)難,、間諜等都是黑客。但是,，為了聚焦,，本文以常言的“網(wǎng)絡(luò)黑客”為主要研究對象，雖然這里的結(jié)果和研究方法其實適用于所有黑客,。
黑客的攻擊肯定是有代價的,，這種代價可能是經(jīng)濟(jì)代價、政治代價或時間代價,。同樣，黑客想要達(dá)到的目標(biāo)也可能是經(jīng)濟(jì)目標(biāo),、政治目標(biāo)或時間目標(biāo),。因此，至少可以粗略地將黑客分為經(jīng)濟(jì)黑客,、政治黑客和時間黑客,。
經(jīng)濟(jì)黑客：只關(guān)注自己能否獲利，并不在乎是否傷及對方,。有時,，自己可以承受適當(dāng)?shù)慕?jīng)濟(jì)代價，但是,，整體上要贏利,。賠本的買賣是不做的，他們肯定不是“活雷鋒”,。因此,，經(jīng)濟(jì)黑客的目標(biāo)就是：以最小的開銷來攻擊系統(tǒng)，并獲得最大的收益,。只要準(zhǔn)備就緒,，經(jīng)濟(jì)黑客隨時可發(fā)動進(jìn)攻。
政治黑客：不計代價，一定要傷及對方要害,，甚至有時還有更明確的攻擊目標(biāo),，不達(dá)目的不罷休。他們隨時精確瞄準(zhǔn)目標(biāo),，但是只在關(guān)鍵時刻才“扣動板機(jī)”,。最終成敗取決于若干偶然因素，比如,，目標(biāo)突然移動（紅客突然出新招）,、準(zhǔn)備不充分（對紅客的防御情況了解不夠）或突然刮來一陣風(fēng)（系統(tǒng)無意中的變化）等。
時間黑客：希望在最短的時間內(nèi)攻破紅客的防線,，而且,，使被攻擊系統(tǒng)的恢復(fù)時間盡可能地長。
從純理論角度來看,，其實沒必要去區(qū)分上述三種黑客,。下面為了形象計，也為了量化計,，我們重點(diǎn)考慮經(jīng)濟(jì)黑客,，即，黑客想以最小的經(jīng)濟(jì)開銷來獲取最大的經(jīng)濟(jì)利益,。
1黑客的靜態(tài)描述
先講一個故事：我是一個“臭手”,，面向墻壁射擊。雖然,，我命中墻上任一特定點(diǎn)的概率都為零,，但是，只要板機(jī)一響,，我一定會命中墻上某點(diǎn),，而這本來是一個“概率為零”的事件。因此,，“我總會命中墻上某一點(diǎn)”這個概率為1的事件,，就可以由許多“概率為零的事件（命中墻上某一指定點(diǎn)）”的集合構(gòu)成。
再將上述故事改編成“有限和”情況：我先在墻上畫滿（有限個）馬賽克格子,，那么,，“我總會命中某一格子”這個概率為1的事件，便可以由有限個“我命中任何指定格子”這些“概率很小,，幾乎為零的事件”的集合構(gòu)成,。或者,，更準(zhǔn)確地說,，假設(shè)墻上共有n個馬賽克格子,，那么，我的槍法就可以用隨機(jī)變量X來完整地描述：如果我擊中第i(1≤i≤n)個格子的事件（記為X=i）的概率為pi,，那么,，p1+p2+…+pn=1。
現(xiàn)在,，讓黑客代替“我”,，讓（有限）系統(tǒng)代替那面墻。
安全界有一句老話,，也許是重復(fù)率最高的話,，“安全是相對的，不安全才是絕對的”,?？墒牵^去大家僅將這句話當(dāng)成“口頭禪”,，而沒有意識到它其實是一個很重要的公理,。
安全公理：對任何（有限）系統(tǒng)來說，安全都是相對的,，不安全才是絕對的,，即，“系統(tǒng)不安全,，總可被黑客攻破”這個事件的概率為1,。
根據(jù)該安全公理可知，雖然黑客命中“某一點(diǎn)”（攻破系統(tǒng)的指定部分）的概率幾乎為零,，但是,，黑客“擊中墻”（最終攻破系統(tǒng)）是肯定的，概率為1,。
黑客可以有至少兩種方法在“墻上”畫馬賽克格子：
畫馬賽克格子的第一種辦法：鎖定目標(biāo)，黑客從自己的安全角度出發(fā),，畫出系統(tǒng)的安全經(jīng)絡(luò)圖［1］,，然后，以每個“元誘因”（或“穴位”）為一個“馬賽克格子”,。假如,，系統(tǒng)的安全經(jīng)絡(luò)圖中共有n個“元誘因”，那么,，黑客的（靜態(tài)）攻擊能力就可以用隨機(jī)變量X來完整地描述：如果黑客摧毀第i(1≤i≤n)個“元誘因”,，記為X=i，其概率為pi,，那么,，p1+p2+…+pn=1,。
這種“元誘因馬賽克畫法”的根據(jù)是：系統(tǒng)出現(xiàn)不安全問題的充分必要條件是某個（或某些）“元誘因”不安全［1］。
“元誘因馬賽克”的缺點(diǎn)是參數(shù)體系較復(fù)雜,，但是,，它的優(yōu)點(diǎn)很多，比如,，可以同時適用于多目標(biāo)攻擊,，安全經(jīng)絡(luò)可以長期積累、永遠(yuǎn)傳承等,。根據(jù)安全經(jīng)絡(luò)圖可知,，“安全”同時具有“波”和“粒子”的雙重性質(zhì)，或者說,，具有“確定性”和“概率性”兩種性質(zhì),。更具體地說，任何不安全事件的“元誘因”的“確定性”更濃,，而“素誘因”和“素事件”的“概率性”更濃,。充分認(rèn)識安全的波粒二象性，將有助于深刻理解安全的實質(zhì),，有助于理解《安全通論》的研究方法和思路,。
畫馬賽克格子的第二種辦法：經(jīng)過長期準(zhǔn)備和反復(fù)測試，黑客共掌握了全部n種可能攻破系統(tǒng)的方法,，于是,，黑客的攻擊能力可以用隨機(jī)變量X完整地描述為：當(dāng)黑客用第i種方法攻破系統(tǒng)，記為X=i(1≤i≤n),，其概率為pi,，這里，p1+p2+…+pn=1,，0<pi<1(1≤i≤n),。
說明：能夠畫出這“第二種馬賽克格子”的黑客肯定是存在的，比如,，長期以“安全檢測人員”這種紅客身份掩護(hù)著的臥底,，就是這類黑客的代表。雖然,，必須承認(rèn),，要想建立完整的武器庫，即,，掌握攻破系統(tǒng)的全部攻擊方法,，或完整地描述上述隨機(jī)變量X，確實是非常困難的,，但是,，從理論上看是可行的,。
當(dāng)然，也許還有其他方法來畫“馬賽克格子”,，不過它們的實質(zhì)都是一樣的,，即，黑客可以靜態(tài)地用一個離散隨機(jī)變量X來描述,，這里X可能取值為{1,，2，…,，n},，概率Pr(X=i)= pi，并且p1+p2+…+pn=1,。
2黑客的動態(tài)描述
黑客的動態(tài)行為千變?nèi)f化,，首先必須清理場景，否則,，根本無法下手,。
為使相關(guān)解釋更形象，本節(jié)采用上述第一種“馬賽克格子畫法”,，即,，黑客是一個離散隨機(jī)變量，他攻破第i個“元誘因”（記為X=i,，1≤i≤n)的概率為pi,，這里，p1+p2+…+pn=1,，0<pi<1,，1≤i≤n。特別強(qiáng)調(diào),，其實下面的內(nèi)容適用于包括第二種方法在內(nèi)的所有“馬賽克格子畫法”,。
任何攻擊都是有代價的，并且,，如果黑客的技術(shù)已經(jīng)足夠好,，那么，整體上來說是“投入越多,，收益越多”。
設(shè)黑客攻破第i個“元誘因”的“投入產(chǎn)出比”為di(1≤i≤n),，即,，若為攻擊第i個“元誘因”黑客投入了1元錢，那么,，一旦攻擊成功（其概率為pi）后,，黑客將獲得di元的收入,；當(dāng)然，如果攻擊失敗,，那么,，黑客的這1塊錢就全賠了。
根據(jù)文獻(xiàn)［1］可知,，任何一個“元誘因”被攻破后,，系統(tǒng)也就被攻破了，不再安全了,。因此,，為了盡量避免被紅客發(fā)現(xiàn),，盡量少留“作案痕跡”,，我們假定：在攻擊過程中,，黑客只要發(fā)現(xiàn)有一個“元誘因”被攻破了,，那么，他就立即停止本次攻擊,，哪怕繼續(xù)攻破其他“元誘因”還可以獲得額外的收入,，哪怕對其他“元誘因”的“攻擊投資”被浪費(fèi),。
設(shè)黑客共有M元用于攻擊的“種子資金”,，如果他把這些資金全部投入到攻擊他認(rèn)為最有可能成功的某個“元誘因”（比如最大的那個pi）,，那么,，假如黑客最終成功地攻破了第i個“元誘因”（其概率為pi）,，則此時黑客的資金總數(shù)就變成Mdi,，但是，假如黑客攻擊失?。ㄆ涓怕蕿?-pi），則他的資金總數(shù)就瞬間變成了零,?？梢?，從經(jīng)濟(jì)上來說,，黑客的這種“孤注一擲”戰(zhàn)術(shù)的風(fēng)險太大，不宜采用,。
為增加抗風(fēng)險能力,，黑客改變戰(zhàn)術(shù),，將他的全部資金分成n部分，b1,、b2、…,、bn，其中bi是用于攻擊第i個“元誘因”的資金在總資金中所占的比例數(shù),，于是，∑ni=1bi=1,，這里0≤bi≤1。如果在本次攻擊中，第i個“元誘因”首先被攻破（其概率為pi），那么,，本次攻擊馬上停止，此時,，黑客的總資產(chǎn)變?yōu)镸bidi，同時,，投入到攻擊其他“元誘因”的資金都白費(fèi)了。由于∑ni=1pi=1,，即,，肯定有某個“元誘因”會被首先攻破，所以,，只要每個bi>0，那么,，本次攻擊結(jié)束后，黑客的總資產(chǎn)肯定不會變成零,，因此，其抗風(fēng)險能力確實增強(qiáng)了,。
我們還假定：為了躲開紅客的對抗，黑客選擇紅客不在場時才發(fā)起攻擊,，比如,，黑客每天晚上對目標(biāo)系統(tǒng)進(jìn)行（一次）攻擊,。當(dāng)然,，這里還有一個暗含的假設(shè),，即，黑客每天晚上都能夠成功地把系統(tǒng)攻破一次,，其實,，這個假設(shè)也是合理的,，因為,，如果要經(jīng)過K個晚上的艱苦攻擊才能攻破系統(tǒng)，那么,，把這K天壓縮成“一晚”就行了,。
單看某一天的情況,，很難對黑客的攻擊戰(zhàn)術(shù)提出任何建議。不過,，如果假定黑客連續(xù)m天晚上對目標(biāo)系統(tǒng)進(jìn)行“每日一次”的攻擊,，那么，確實存在某種攻擊戰(zhàn)術(shù),，能使得黑客的盈利情況在某種意義上達(dá)到最佳,。
為簡化下足標(biāo),，本文對bi和b(i)交替使用,，不加區(qū)別。
如果黑客每天晚上都對他的全部資金按相同的分配比例b=(b1,b2,…,bn)來對系統(tǒng)的各“元誘因”進(jìn)行攻擊,。那么，m個晚上之后,，黑客的資產(chǎn)就變?yōu)椋?/p>
這里S(X)=b(X)d(X),，Xi是1~n之間的某個正整數(shù),，它表示在第i天晚上，被（首先）攻破的那個“元誘因”的編號,，所以，X1,、X2、…、Xm是獨(dú)立同分布的隨機(jī)變量,，設(shè)該分布是p(x),，于是有如下定理：
定理1若每天晚上黑客都將其全部資金按比例b=(b1,b2,…,bn)分配，來對系統(tǒng)的各“元誘因”進(jìn)行攻擊,，那么,，m天之后，黑客的資產(chǎn)就變?yōu)椋?/p>
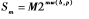
這里
稱為“雙倍率”,。
證明：由于獨(dú)立隨機(jī)變量的函數(shù)也是獨(dú)立的,，所以，
也是獨(dú)立同分布的,，由弱大數(shù)定律,，可得：
于是，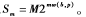
證畢,。
由于黑客的資產(chǎn)按照2mw(b,p)的方式增長（這也是把W(b,p)稱為“雙倍率”的根據(jù)），因此,，只需要尋找某種資金分配戰(zhàn)術(shù)b=(b1,b2,…,bn),，使得雙倍率W(b,p)最大即可,。
定義1如果某種戰(zhàn)術(shù)分配b,，使得雙倍率W(b,p)達(dá)到最大值W*(p),，那么，就稱該值為最優(yōu)雙倍率,，即：
這里的最大值max是針對所有可能的滿足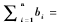
而取的。
雙倍率W(b,p)作為b的函數(shù),，在約束條件∑ni=1bi=1下,，求其最大值,?？梢詫懗鋈缦吕窭嗜粘俗雍瘮?shù)并且改變對數(shù)的基底（這不影響最大化b）,，則有：
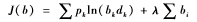
關(guān)于bi求導(dǎo)得到：
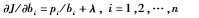
為了求得最大值，令偏導(dǎo)數(shù)為0,，從而得出：
將它們帶入約束條件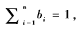
可得到λ=-1和bi=pi,。從而可知,，b=p為函數(shù)J(b)的駐點(diǎn),。
定理2最優(yōu)化雙倍率
并且,，按比例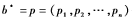
分配攻擊資金的戰(zhàn)術(shù)進(jìn)行攻擊，便可以達(dá)到該最大值,。這里H(p)是描述靜態(tài)黑客的那個隨機(jī)變量的熵，即,，
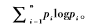
證明：將雙倍率W(b,p)重新改寫，使得容易看出何時取最大值：
這里D(p|b)是隨機(jī)變量p和b的相對熵［7］,。而當(dāng)b=p時,，可直接驗證上述等式成立。證畢,。
從定理2可知：對于一個可用離散隨機(jī)變量X（Pr(X=i)= pi,，并且，p1+p2+…+pn=1）來靜態(tài)描述的黑客,，他的動態(tài)最佳攻擊戰(zhàn)術(shù)也是（p1,p2,…,pn）,，即，將攻擊資金按比例（p1,p2,…,pn）分配后,，可得到最多的“黑產(chǎn)收入”,。
下面再對定理2進(jìn)行一些更細(xì)致的討論，有：
定理3如果攻破每個“元誘因”的投入產(chǎn)出比是相同的,，即,，各個di彼此相等，都等于a,，那么此時的最優(yōu)化雙倍率W*(p)=loga-H(p),，即,，最佳雙倍率與熵之和為常數(shù)，并且,，若按比例b*=p分配攻擊資金,，那么，此種戰(zhàn)術(shù)的攻擊業(yè)績便可達(dá)到最大值,。此時,，第m天之后，黑客的財富變成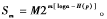
而且,，黑客的熵若減少1比特,，那么，他的財富就會翻一倍,！
如果并不知道每個di的具體值,，而只知道∑1/di=1，此時,，記ri=1/di,于是,，雙倍率可以重新寫為：
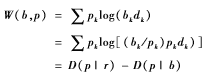
由此可見雙倍率與相對熵之間存在著非常密切的關(guān)系。
由于黑客每天晚上都要攻擊系統(tǒng),，他一定會總結(jié)一些經(jīng)驗來提高攻擊效果,。更準(zhǔn)確地說，可以假設(shè)黑客知道了攻破系統(tǒng)的某種邊信息Y,，它也是一個隨機(jī)變量,。
設(shè)X∈{1,2,…,n}為第X個“元誘因”，攻破它的概率為p(x),，而攻擊它的投入產(chǎn)出比為d(x),。設(shè)（X，Y）的聯(lián)合概率密度函數(shù)為p(x,y),。用b(x|y)≥0,，∑xb(x|y)=1記為已知邊信息Y的條件下，黑客對攻擊資金的分配比例,。此處b(x|y)理解為：當(dāng)?shù)弥畔的條件下,，用來攻擊第x個“元誘因”的資金比例。對照前面的記號,，將b(x)≥0,，
表示為無條件下，黑客對攻擊資金的分配比例,。
設(shè)無條件雙倍率和條件雙倍率分別為：
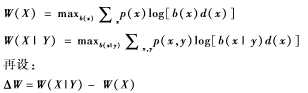
對于獨(dú)立同分布的“攻擊元誘因”序列(Xi,Yi),，可以看到：當(dāng)具有邊信息Y時，黑客的相對收益增長率為2mw(X|Y),；當(dāng)黑客無邊信息時,，他的相對收益增長率為2mw(X),。
定理4由于獲得攻擊“元誘因”X的邊信息Y，而引起的雙倍率增量ΔW滿足ΔW=I（X,；Y）,。這里I（X；Y）是隨機(jī)變量X和Y的互信息,。
證明：在有邊信息的條件下,，按照條件比例分配攻擊資金，即,，b*(x|y)=p(x|y),，那么關(guān)于邊信息Y的條件雙倍率W(X|Y)可以達(dá)到最大值。于是：
當(dāng)無邊信息時,，最優(yōu)雙倍率為：
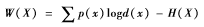
從而,，由于邊信息Y的存在，而導(dǎo)致的雙倍率的增量為：
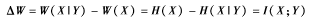證畢,。
此處雙倍率的增量正好是邊信息Y與“元誘因”X之間的互信息,。因此，如果邊信息Y與“元誘因”X相互獨(dú)立,，那么,，雙倍率的增量就為0。
設(shè)Xk是黑客第k天攻破的“元誘因”的序號,，假如各{Xk}之間不是獨(dú)立的,，又假設(shè)每個dk彼此相同，都等于a,。于是,，黑客根據(jù)隨機(jī)過程{Xk}來決定第（k+1）天的最佳攻擊資金分配方案（即最佳雙倍率）為：
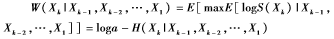
這里的最大值max是針對所有滿足如下條件的邊信息攻擊資金分配方案而取的：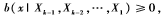
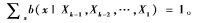
而且，該最優(yōu)雙倍率可以在
時達(dá)到,。
第m天晚上的攻擊結(jié)束后，黑客的總資產(chǎn)變成:
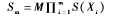
并且,，其增長率的指數(shù)為:
這里［H(X1,X2,…,Xm)］/m是黑客m天攻擊的平均熵,。對于熵率為H(χ)的平衡隨機(jī)過程，對上述增長率指數(shù)公式的兩邊取極限,，可得:
這再一次說明,，熵率與雙倍率之和為常數(shù)。
3結(jié)束語
文獻(xiàn)［1］~［6］奠定了《安全通論》的兩個重要基石：安全經(jīng)絡(luò),、安全攻防,。本文開始，我們將努力奠定《安全通論》的第三塊重要基石：黑客,。
沒有黑客就沒有安全問題,，也更不需要《安全通論》,。可惜,，黑客不但有,，還越來越多，而且其外在表現(xiàn)形式還千奇百怪,，因此，有必要專門對黑客進(jìn)行系統(tǒng)深入的研究。
本文雖然徹底解決了黑客的靜態(tài)描述問題,，即,，黑客其實就是一個隨機(jī)變量X，它（他）的破壞力由X的概率分布函數(shù)F(x)(或概率密度函數(shù)p(x))來決定,。但是,，關(guān)于黑客的動態(tài)描述問題，還遠(yuǎn)未解決,，本文只是在若干假定之下,，給出了黑客攻擊的最佳戰(zhàn)術(shù)。歡迎有興趣的讀者來研究黑客的其他攻擊行為的最佳戰(zhàn)術(shù),。
參考文獻(xiàn)
?。?］ 楊義先，鈕心忻.安全通論（1）——經(jīng)絡(luò)篇［J］.微型機(jī)與應(yīng)用,，2016,，35（15）：1 4.
［2］ 楊義先,，鈕心忻.安全通論（2）——攻防篇之“盲對抗”［J］.微型機(jī)與應(yīng)用,，2016，35（16）：1 5.
?。?］ 楊義先,，鈕心忻.安全通論（3）——攻防篇之“非盲對抗”之“石頭剪刀布”［J］.微型機(jī)與應(yīng)用，2016,，35（17）：1 3.
?。?］ 楊義先，鈕心忻.安全通論（4）——攻防篇之“非盲對抗”之“童趣游戲”［J］.微型機(jī)與應(yīng)用,，2016,，35（18）：3 5,9.
［5］ 楊義先,，鈕心忻.安全通論（5）——攻防篇之“非盲對抗”之“勸酒令”［J］.微型機(jī)與應(yīng)用,，2016，35（19）：2 6.
［6］ 楊義先,，鈕心忻.安全通論（6）——攻防篇之“多人盲對抗”［J］.微型機(jī)與應(yīng)用,，2016，35（20）：1 4.
?。?］ COVER T M,，THOMAS J A.信息論基礎(chǔ)［M］.阮吉壽，張華,，譯.北京：機(jī)械工業(yè)出版社,，2007.