朱進(jìn)勇,王立冬

　?。ㄜ娦倒こ虒W(xué)院 電子與光學(xué)工程系,，河北 石家莊 050003）

       摘要：在無線電測向領(lǐng)域，相干信號對測向精度和分辨性能有著較大影響,，如果將相干信號和多徑信號之間的關(guān)系相互混淆,，會產(chǎn)生較大的測向誤差。首先建立了空地多徑效應(yīng)三徑模型,，對多徑信號之間的關(guān)系和多徑信號對測向的影響進(jìn)行具體分析,；采用相關(guān)性理論，對信號的相干性進(jìn)行了詳細(xì)分析,，進(jìn)而討論了多徑信號的相干性,；最后，在SystemVue軟件環(huán)境下對空地多徑效應(yīng)三徑模型進(jìn)行了仿真建模,，由仿真結(jié)果得出了多徑信號之間的相干規(guī)律及其對測向的影響規(guī)律,。

　　關(guān)鍵詞：相干信號,；多徑效應(yīng)；測向,；SystemVue軟件

　　中圖分類號：TN95 ;TN97文獻(xiàn)標(biāo)識碼：ADOI：10.19358/j.issn.16747720.2016.20.004

　　引用格式：朱進(jìn)勇,王立冬. 多徑信號的相干性及對測向的影響［J］.微型機(jī)與應(yīng)用,，2016,35（20）：17 20，24.

0引言

　　在電磁波的傳播過程中,，由于自然環(huán)境的多變性和復(fù)雜性,，導(dǎo)致進(jìn)入接收機(jī)的信號中存在相干信號。相干信號的干擾分為同頻干擾和多徑干擾,，同頻干擾［1］是臨近同頻段的雷達(dá)所發(fā)射的信號進(jìn)入接收機(jī)后產(chǎn)生的干擾,；多徑干擾是由于背景物體的反射造成信號的傳播存在多種路徑,，在接收機(jī)處相互疊加而產(chǎn)生的干擾。相干信號源的存在會導(dǎo)致接收機(jī)的虛警或者目標(biāo)的定位不準(zhǔn)確，甚至出現(xiàn)錯誤,。相干信號對DOA(Direction of Arrival)估計有著不利影響,。例如，傳統(tǒng)的超分辨測向算法［2］ (MUSIC)對相干信號沒有效果,。文獻(xiàn)［3］對信號的相關(guān)性進(jìn)行了分析，并對相關(guān)信號和不相關(guān)信號進(jìn)行了DoA估計的仿真,，但是其仿真的條件比較理想化,，沒有基于實際測向環(huán)境進(jìn)行分析,，所以其結(jié)論應(yīng)該只適用于頻率和初始相位都相同的信號；文獻(xiàn)［4］對反射路徑電場強(qiáng)度的理論分析沒有考慮反射時的能量損耗,，所以其得到的角度偏差值也存在誤差,。

　　本文建立了空地多徑效應(yīng)三徑模型，分析了多徑信號對測向的影響,，完善了文獻(xiàn)［4］對反射路徑場強(qiáng)的理論計算；采用相關(guān)性理論對信號的相干性進(jìn)行了具體分析，討論了多徑效應(yīng)與相干信號之間的關(guān)系,；最后,，在SystemVue［5］環(huán)境下，建立了完整的空地多徑效應(yīng)三徑模型,，分析了多徑信號之間的相干性及其對測向的影響,。

1多徑效應(yīng)對測向的影響及其相干性分析

　　多徑效應(yīng)［6］是指電磁波在傳播過程中的多徑傳輸現(xiàn)象所引起的干涉時延效應(yīng)。

　　在實際的測向過程中,，接近地面的接收設(shè)備不僅接收由信號源直接傳輸過來的直射信號,，還可能接收到由周圍環(huán)境如高山,、叢林、建筑物等經(jīng)過多路徑反射后的干擾信號,。由于直射信號與多徑反射后的干擾信號頻率相同,，僅僅在相位和信號強(qiáng)弱上有所差別,，因此，接收機(jī)測向系統(tǒng)很容易對這些信號產(chǎn)生誤判,，不能區(qū)分哪個信號是直射信號,，哪個信號是反射后的干擾信號，造成測向不準(zhǔn)確甚至無法得到目標(biāo)方位角信息的現(xiàn)象,。為此,，本文建立了典型的三徑模型，分析了多徑信號對測向的影響及其相干性,。

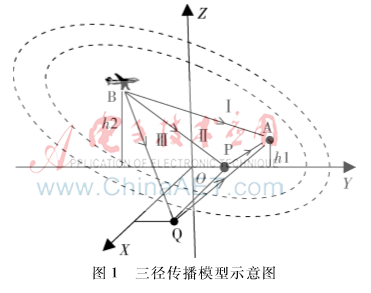
　　圖1所示為空地三徑模型,。其中XOY平面為水平面，Z軸垂直于XOY平面向上,。接收機(jī)A的高度h1,，發(fā)射機(jī)B的高度為h2。為了便于分析,，設(shè)直射傳播路徑BA（用Ⅰ代替）在XOY平面上的投影位于Y軸上,，反射傳播路徑Ⅱ的反射點P也位于Y軸上，反射傳播路徑Ⅲ的反射點Q不在Y軸上,，是任意的一條路徑,。因為路徑Ⅱ在XOY平面上的投影位于Y軸上,，所以它在接收天線處不影響對方位角的測量，但對俯仰角有較大的影響,。路徑Ⅲ對方位角和俯仰角的測量都有影響,。圖中的兩個虛線橢圓是以A和B為焦點的信道橢圓模型［7］，因此,，所有位于同一個虛線橢圓上的反射點所產(chǎn)生的反射波具有相同的傳播路徑長度,，也就是具有相同的時延。

　　根據(jù)自由空間無線電磁波的傳播理論［7-8］可得,，路徑Ⅰ在接收天線處產(chǎn)生的場強(qiáng)為

　　式中,， Pt（kw）為發(fā)射機(jī)天線的輸入功率，G1為發(fā)射天線在直射路徑方向的增益,，d1為直射路徑的距離（km）,。

　　路徑Ⅱ和路徑Ⅲ在地面進(jìn)行了二次反射，可以將反射點當(dāng)作一個點輻射源來分析其產(chǎn)生的場強(qiáng)大小,。其中,，路徑Ⅱ在反射點的場強(qiáng)為

　　根據(jù)平均功率流密度公式

　　得到反射點的反射功率為

　　所以，路徑Ⅱ反射后經(jīng)過d22的距離到達(dá)接收機(jī)處產(chǎn)生的場強(qiáng)為

　　式中,， G21為發(fā)射機(jī)到反射點的增益，G22為反射點到接收機(jī)的增益,，A1為地面對無線電磁波的反射率（草地上的反射率一般為0.4~0.6,，金屬表面的反射率一般為0.8~0.9），d21為發(fā)射機(jī)到反射點的距離,，d22為反射點到接收機(jī)的距離,，η為波阻抗（

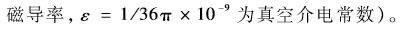
　　同理，可以得到路徑Ⅲ在接收機(jī)處的場強(qiáng)為

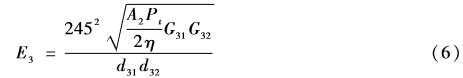
　　其中,， G31為發(fā)射機(jī)到反射點的增益,，G32為反射點到接收機(jī)的增益，A2為地面對無線電磁波的反射率,，d31為發(fā)射機(jī)到反射點的距離,，d32為反射點到接收機(jī)的距離。

　　由式（1）,、（5）和（6）可得,，在接收機(jī)處的總場強(qiáng)為

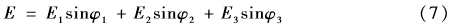
　　式中， φ1,、φ2,、φ3為各路徑的場強(qiáng)方向與大地垂直線方向的夾角。發(fā)射機(jī)與接收機(jī)的水平距離為l,，路徑Ⅲ在X,、Y軸上的投影距離為s和a,。路徑Ⅰ和路徑Ⅱ的場強(qiáng)在XOY平面上投影為

　　路徑Ⅲ在XOY平面上投影為

　　由圖2中的三路徑場強(qiáng)投影圖可以看出，路徑Ⅱ?qū)β窂舰穹轿唤堑臏y量沒有影響,，而路徑Ⅲ使路徑Ⅰ的方位角產(chǎn)生了偏移,。因此，在方位角的角度偏移上只考慮路徑Ⅲ對路徑Ⅰ的影響,。設(shè)偏移角度的弧度值為β,，根據(jù)場強(qiáng)大小可以得到

　　實際測向過程中，容易產(chǎn)生多徑信號,，存在多徑效應(yīng),。由上述分析可得，多徑效應(yīng)對測向?qū)a(chǎn)生較大影響,。

2多徑信號的相干性分析

　　設(shè)兩個信號X1,、X2的相關(guān)程度采用相關(guān)系數(shù)［9-10］ρ來衡量，其定義為

　　式中cov(X1,X2)為兩個信號的協(xié)方差函數(shù),，E(X)為數(shù)學(xué)期望,，μ(t)和D(X)分別為兩信號的均值函數(shù)和方差函數(shù)。當(dāng)ρ=0時,，兩信號不相關(guān),；當(dāng)0<|ρ|<1時，兩信號相關(guān),；當(dāng)|ρ|=1時,，兩信號相干。設(shè)w1和w2為信號X1和X2的頻率,，φ1和φ2為兩信號的初始相位,，其相關(guān)系數(shù)表示為

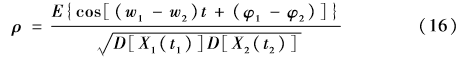
　　式中恒大于0，由式（16）可得：

　?。?）w1≠w2時,， ρ=0，即兩個頻率不同的信號是不相關(guān)的,；

　?。?）w1=w2時，若φ1=φ2以及兩相位差180°,，則|ρ|=1,，兩信號為相干信號；若兩相位差為90°或270°,，則ρ=0,，兩信號不相關(guān)；若兩信號的相位差不屬于以上兩種特殊情況,，0<|ρ|<1,，則兩信號相關(guān),，但不相干。

　　由第1節(jié)中多徑信號的三徑模型分析以及上述相關(guān)性理論分析可知,，多徑信號的頻率相同,，但是由于其相位關(guān)系的不同，它們可能是相干的,，也可能是不相干的,。多徑信號中，當(dāng)兩信號的相位相同或者相位差為180°時,，兩信號為相干信號,；當(dāng)兩信號的相位差為90°或270°時，兩信號相互獨立,；當(dāng)兩信號的相位差不屬于這兩種情況時,，兩信號相關(guān)但不相干。

3多徑效應(yīng)的SystemVue仿真系統(tǒng)設(shè)計

　　利用SystemVue軟件構(gòu)建空地多徑效應(yīng)模型,，可以定量仿真分析多徑信號的相干性及其對測向的影響,。空地多徑效應(yīng)三徑模型測向系統(tǒng)由發(fā)射機(jī)系統(tǒng),、路徑Ⅰ,、路徑Ⅱ,、路徑Ⅲ以及MUSIC算法處理部分組成,。

　　為了深入分析該測向系統(tǒng),，將多徑模型測向系統(tǒng)分為發(fā)射機(jī)系統(tǒng)和地面接收機(jī)系統(tǒng),，如圖3和圖4所示,。

　　圖3中,，RADAR_LFM模塊產(chǎn)生所需要的線性調(diào)頻信號,，信號形式PW為30 μs,，脈沖重復(fù)頻率PRI為104 Hz,，帶寬BW為5 MHz；該信號通過Set Sample Rate采樣模塊變?yōu)殡x散化的信號形式,；該離散化的信號通過RADAR_Tx_DBS模塊形成陣列信號的數(shù)字波束,；該數(shù)字波束信號通過RADAR_MultiCH_Tx模塊，實現(xiàn)多信道的發(fā)射,；并通過RADAR_PhaseArrayTx模塊,，完成仿真發(fā)射電子掃描陣列［11］（ESAs）。ESAs能夠提供可控制的,、角度化的,、高增益的波束。與傳統(tǒng)的反射面天線相比,，ESAs能夠在空間電子地掃描陣列波束,，而不需要通過物理地移動陣列,，其微秒級掃描波束在精度上遠(yuǎn)高于反射面天線的毫秒級掃描波束。

　　圖4為路徑Ⅰ的接收線路,。從信號源到來的電磁波通過RADAR_PhaseShift模擬模塊產(chǎn)生從遠(yuǎn)區(qū)電場到觀測點的數(shù)字陣列天線的相移,，即可以設(shè)置二維陣列天線中X軸8個陣元為Y軸1個陣元，陣元之間的間距為半波長,，遠(yuǎn)區(qū)電場觀測點與信號源之間的方位角設(shè)為20°,；然后，RADAR_MultiCH_Rx模塊對數(shù)字陣列天線的信號進(jìn)行接收處理,；最后,，Commutator模塊對接收后的8路信號進(jìn)行整流處理，得到一路信號,。

　　路徑Ⅱ的接收路線與路徑Ⅰ相類似,，只是在RADAR_PhaseShift模塊前面設(shè)置一個Delay模塊和Gain模塊。Delay模塊參數(shù)設(shè)置為10,，相當(dāng)于延遲時間為1 μs,，即電磁波經(jīng)反射后路徑Ⅱ相對于路徑Ⅰ多傳播了300 m；Gain模塊的參數(shù)設(shè)置為0.005,，相當(dāng)于副瓣經(jīng)過反射后的衰減（草地上的反射率為0.4~0.6）,；該路徑中，RADAR_PhaseShift模塊的角度設(shè)置與路徑Ⅰ相同,，相當(dāng)于路徑Ⅱ不影響直射路徑的方位角測量,。

　　路徑Ⅲ與路徑Ⅱ 類似，只需要作以下修改：將Delay模塊的參數(shù)設(shè)置為20,，相當(dāng)于延遲時間為2 μs,，即反射后的路徑Ⅲ比路徑Ⅰ多傳播了600 m；方位角的角度設(shè)置為25°,。

　　完成以上設(shè)置后,，將3路信號送入Add模塊整合為一路信號；將該信號送入Pack_M模塊,，實現(xiàn)8行1 024列的矩陣打包,；最后，MathLang模塊采用經(jīng)典的MUSIC算法對矩陣包（三路信號）進(jìn)行波達(dá)方向角估計,，分析多徑信號的相干性及其對測向的影響,。

4仿真結(jié)果分析

　　在SystemVue軟件仿真平臺上運行上述多徑模型測向系統(tǒng)，可得如圖5~圖10所示的仿真結(jié)果,。

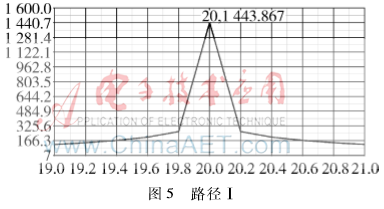
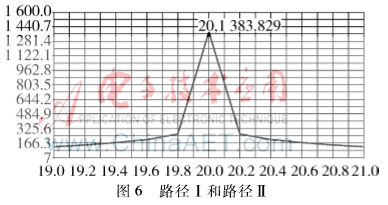
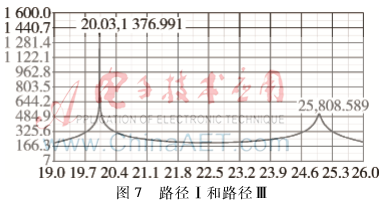
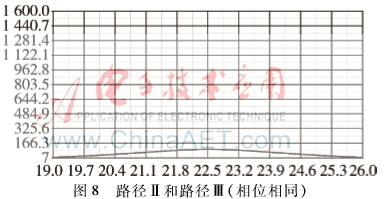
　　圖5為路徑Ⅰ的測向波形圖,，在該波形圖可以看到只有一個尖峰；圖6為路徑Ⅰ和路徑Ⅱ兩條路徑共同作用的波形圖,，該圖中仍然只能見到一個尖峰,；圖7為路徑Ⅰ和路徑Ⅲ兩條路徑的波形圖,，該圖中可見到兩個尖峰。其中,，第一個尖峰為路徑Ⅰ產(chǎn)生的,，第二個尖峰為路徑Ⅲ產(chǎn)生的。相對于第一個尖峰,，第二個尖峰較平緩,，幅度值較小。由圖5~圖7得到的具體參數(shù)值如表1所示,。由表1中的數(shù)據(jù)可以得出：

　?。?）路徑Ⅰ和路徑Ⅱ兩條路徑共同作用時的尖峰幅度值小于路徑Ⅰ的幅度值。這說明多徑信號進(jìn)入接收機(jī)導(dǎo)致接收信號衰落,。

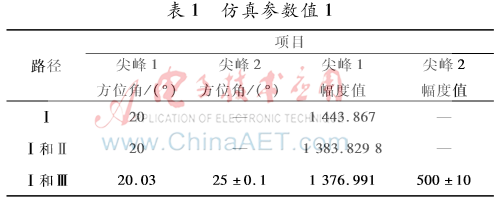
　?。?）路徑Ⅰ和路徑Ⅲ為同頻不同相位，經(jīng)典的MUSIC算法能夠明顯地將兩路多徑信號分辨開來,。由于MUSIC算法對相干信號無效,，因此路徑Ⅰ和路徑Ⅲ這兩種同頻不同相位的信號不是相干信號。這與前面的理論分析是一致的,。

　?。?）圖7中，路徑Ⅰ所測得方位角為20.03°,，與實際方位角度值20°有0.03°的差值,，與上文理論分析中的β值乘以180/π（弧度轉(zhuǎn)化為角度）后的角度偏差值是一個數(shù)量級，這是誤差允許范圍內(nèi)的,。

　　圖8為路徑Ⅱ和路徑Ⅲ在相位相同情況下的波形圖,，在該圖中完全不能見到任何峰值的點，整個波形平緩,；圖9為路徑Ⅱ和路徑Ⅲ在相位不相同情況下的波形圖,，在該圖中能夠見到路徑Ⅱ和路徑Ⅲ的兩個峰值，但是幅度值較?。粓D10為 路徑Ⅰ,、路徑Ⅱ和路徑Ⅲ同頻但不同相位的波形圖,，圖中能夠見到兩個峰值，第一個峰值很尖銳,，為路徑Ⅰ和路徑Ⅱ疊加以及路徑Ⅲ對其測向的影響所產(chǎn)生的,，第二個尖峰為路徑Ⅲ所產(chǎn)生的，其幅度值相對第一個尖峰較小,，其尖峰也相對平緩,。由圖8~圖10得到的具體參數(shù)值如表2所示,。

　　從表2中的數(shù)據(jù)可以看出：

　　（1）MUSIC算法不能夠?qū)⒙窂舰蚝吐窂舰笙辔幌嗤男盘柗直骈_來,，而可以將相位不同的兩信號分辨開來,。這說明同頻同相位的信號為相干信號，同頻不同相位的信號為不相干信號,；多徑效應(yīng)產(chǎn)生的相干信號對測向有著嚴(yán)重的影響,，尤其是采用MUSIC算法，這類特征值分解類算法時,，測向分辨效果很差,。

　　（2）圖10中,，路徑Ⅰ和路徑Ⅱ共同作用的路徑受到路徑Ⅲ影響所得到的方位角度值為20.04°,，與上文理論分析所得到的角度偏差值也是在一個數(shù)量級的，這是在誤差允許范圍內(nèi)的,。

5結(jié)論

　　本文建立了多徑效應(yīng)的三徑模型,，分析了多徑信號對測向的影響，得到了測向誤差理論公式,；推導(dǎo)了多徑信號相關(guān)性分析公式,，對多徑信號的相干性進(jìn)行了理論分析；在SystemVue仿真環(huán)境下,，采用空地多徑效應(yīng)三徑模型,，仿真分析了多徑信號與相干信號之間的關(guān)系以及相干信號對測向的影響。由仿真結(jié)果可得,，多徑信號由于經(jīng)歷了反射環(huán)境的變化導(dǎo)致了接收信號的衰落,；經(jīng)過反射后的信號會對直射路徑信號的測向產(chǎn)生影響；多徑信號中的同頻同相位信號是相干信號,，而同頻不同相位信號不是相干信號,，且多徑信號將嚴(yán)重影響特征值分解類算法的測向分辨效果。該規(guī)律對設(shè)計測向算法,、提高測向精度具有一定的指導(dǎo)意義,。

　　參考文獻(xiàn)

　　［1］ 毛滔,，曾浩.雷達(dá)抗同頻干擾方法研究［J］.航天電子對抗,，2005，21(6)：43-45.

　?。?］ SCHMIDT R. O. Multiple emitter location and signal parameter estimation［J］.IEEE Transactions on Antennas and Propagation, 1986,34(3):276-280.

　?。?］ 熊波，李國林，尚雅玲,，等.信號相關(guān)性與DOA估計［J］.電子科技大學(xué)學(xué)報,， 2007，36(5):907-910.

　?。?］ 李博章,，謝飛，劉坤.多徑效應(yīng)對測向方位角的影響分析［J］.船舶電子工 程,， 2010,，30(2):81-83,110.

　　［5］ DAVID L, ANURAG B. Radar system design and interference analysis using Agilent SystemVue ［Z］.Agilent Technologies Application Note,2010.

　?。?］ 毛虎,，楊建波，邱宏坤.多徑效應(yīng)對信號接收及方向測量的影響［J］.電訊技術(shù),，2010,，50(10):63-68.

　　［7］ 封吉平,，曾瑞,，梁玉英.微波工程基礎(chǔ)［M］.北京：電子工業(yè)出版社，2002.

　?。?］ 丁鷺飛,，耿富錄.雷達(dá)原理（第3版）［M］.西安：西安電子科技大學(xué)出版社，1995.

　?。?］ 張玉憲,，魏少明.多徑效應(yīng)對無源定位性能的影響［J］.電子測量技術(shù)，2009,，32(7):18-21.

　?。?0］ 謝飛，張忠臣,，張鵬,，等.多徑效應(yīng)對測向誤差的影響［J］.電子測量技術(shù)，2010,，33(1):29-31,39.

　?。?1］ 薛正輝，李偉明,，任武.陣列天線分析與綜合［M］.北京：北京航空航天大學(xué)出版社,，2011.