文獻(xiàn)標(biāo)識碼: A
文章編號: 0258-7998(2015)03-0101-04
0 引言
假設(shè)盲源分離的源信號個數(shù)為J,接收傳感器的個數(shù)為R,盲源分離可以分為超定盲源分離(J≥R)和欠定盲源分離(J<R)兩種情況。大多數(shù)盲分離算法都假設(shè)接收傳感器個數(shù)不少于源信號個數(shù),然而在實際應(yīng)用中,接收傳感器個數(shù)往往有限,有時會出現(xiàn)接收傳感器小于接收源信號個數(shù)的欠定混合情況(Underdetermined Blind Source Separation,UBSS)。欠定盲源分離一般分為兩步:(1)分離混合矩陣;(2)恢復(fù)源信號。本文只考慮對混合矩陣的估計。
針對欠定盲源分離問題,大多數(shù)文獻(xiàn)提出的算法是將觀測信號在時域或頻域稀疏化,這勢必會產(chǎn)生龐大的計算量,并且應(yīng)用范圍局限于觀測信號和源信號數(shù)量較少的情況。考慮到源信號一般均滿足相互獨立和具有時間結(jié)構(gòu)等特性,L.De Lathauwer提出了二階欠定盲辨識算法(Second-order Blind Identification of Underdetermined Mixtures,SOBIUM)[1],該方法不要求源信號在時域或變換域是稀疏的,通過對觀測信號的時延協(xié)方差矩陣組成三階張量直接進(jìn)行平行因子分解實現(xiàn)對混合矩陣的估計。TICHAVSKY P在SOBIUM的基礎(chǔ)上提出了加權(quán)欠定混合矩陣盲分離算法[2],該算法通過加權(quán)張量分解來完成混合矩陣的估計,提高了分離信號的信干比,但是SOBIUM的迭代收斂時間較長,而且可能產(chǎn)生局部收斂。
針對以上問題,本文在SOBIUM方法的基礎(chǔ)上,加入了增強(qiáng)線搜索算法(Enhanced Line Search,ELS) 。ELS可以顯著改善最小二乘法的性能,降低局部收斂的風(fēng)險,更重要的是減少了迭代次數(shù),并且復(fù)雜度不高。
1 欠定盲分離與PARAFAC分解
1.1 瞬時欠定盲源分離模型
瞬時混合模型下的欠定盲源分離,其含噪混合模型為:
X(t)=AS(t)+N(t) t=1,…,T (1)
其中,X(t)=[x1(t),x2(t),…,xR(t)]T為R維接收信號矢量,A表示一個未知的J×R的混合矩陣,S(t)=[s1(t),s2(t),…,sR(t)]T為R維源信號矢量,N(t)=[n1(t),…,nR(t)]T為R維噪聲矢量,(*)T代表轉(zhuǎn)置。在噪聲不存在或者可以忽略不計的情況下,式(1)可以化簡為:
X(t)=AS(t)(2)
1.2 PARAFAC分解
平行因子(Parallel Factor,PARAFAC)分析又叫標(biāo)準(zhǔn)分解,是三面或更高面陣低秩分解的總稱。平行因子分解在多個應(yīng)用領(lǐng)域發(fā)揮著有廣泛的作用,遠(yuǎn)遠(yuǎn)超出了化學(xué)計量學(xué)。平行因子分析在信號處理和通信領(lǐng)域中的數(shù)據(jù)域和子空間域[1-2]表現(xiàn)出良好的實用性,觀測數(shù)據(jù)被轉(zhuǎn)換為張量形式進(jìn)行運算。下面給出關(guān)于平行因子的定義:
定義1:若矩陣A的任意kN個列線性獨立,則最大kN的值稱之為矩陣A的Kruskal秩,簡稱k秩。
定義2:如果一個張量X∈RI×J×K等于三個向量a,b,c的外積,則這個張量的秩為1。
定義3:一個三階張量X∈RI×J×K可以寫成秩為1的張量的最小數(shù)量的線性組合,叫作平行因子分解。這一最小數(shù)量(源信號數(shù)N)等于張量X的秩(可用于對源信號數(shù)的估計)即:
式中ar、br、cr分別代表矩陣A∈CI×R、B∈CJ×R和C∈CK×R的第r列。其中xijk=ai bj ck,i=1,…,I,j=1,…,J,k=1,…,K。
平行因子分解的矩陣模式可以寫為:
X(1)=(B⊙C)AT,X(1)∈CJK×I
X(2)=(C⊙A)BT,X(2)∈CKI×J
X(3)=(A⊙B)CT,X(3)∈CIJ×K(4)
平行因子的唯一性在文獻(xiàn)[3-5]中進(jìn)行了研究,可以總結(jié)為下面的定理:
定理1:如果滿足
kA+kB+kC≥2R+2(5)
則平行因子分解唯一。kA、kB、kC分別代表矩陣A、B、C的秩。R為源信號的個數(shù)。
用平行因子分解解決欠定盲分離混合矩陣問題時,源信號個數(shù)J與接收傳感器最大個數(shù)Rmax的關(guān)系如表1所示。

1.3 PARAFAC分解估計欠定混合矩陣
若源信號為零均值且互不相關(guān)的非平穩(wěn)信號,那么源信號在t時刻的二階自相關(guān)矩陣可表示為:
式中DN=Est s■■是塊對角陣,n=1,…,N,N是分塊的個數(shù),矩陣A稱為分塊成型矩陣。式(3)中時間延時?子n可以為零,上標(biāo)T表示轉(zhuǎn)置。
將矩陣組{RN}轉(zhuǎn)為(d,d,M)維的三階張量形式:
其中θ代表一個影響矩陣A和D的所有元素的參數(shù)向量。![7GH1GV}37L67JY$S{P]TKYM.png 7GH1GV}37L67JY$S{P]TKYM.png](http://files.chinaaet.com/images/2017/01/11/6361973134115400008951315.png)
式中R代表張量,R為源信號的數(shù)目,⊙表示張量的外積,{an}和{dn}分別為A和D的列向量,上標(biāo)*代表共軛轉(zhuǎn)置。
2 加權(quán)增強(qiáng)最小二乘法
2.1 交替最小二乘法算法
張量的標(biāo)準(zhǔn)分解通常使用三線性交替最小二乘(Alternating Least Squares,ALS)算法實現(xiàn)。迭代過程中的代價函數(shù)為:
||·||F表示Frobenius矩陣范數(shù)。ALS的目標(biāo)是在每一步迭代中,使張量R與它的當(dāng)前估計值的差的范數(shù)最小。用于平行因子分析模型擬合的 ALS 過程即在固定上次迭代獲取的部分矩陣估計值基礎(chǔ)上, 估計其他矩陣, 該交錯映射形式的最小二乘回歸過程循環(huán)下去, 直至收斂。矩陣A、B和C的估計可以表示為:
其中上標(biāo)“+”代表Moore-Penrose偽逆。
2.2 增強(qiáng)的線搜索(ELS)
通常在數(shù)據(jù)量非常大,或當(dāng)兩個因素幾乎共線時,ALS的收斂性是非常緩慢的[6]。壓縮和線搜索是應(yīng)對收斂慢問題的兩種解決方案。本文采用增強(qiáng)線搜索來加快ALS: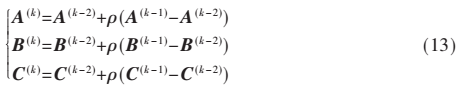
上式中上標(biāo)(k)、(k-1)、(k-2)分別代表第k次,第k-1次,第k-2次迭代。令:
其中![S2~VCV@MIRA]IXAHDH(MOTS.png S2~VCV@MIRA]IXAHDH(MOTS.png](http://files.chinaaet.com/images/2017/01/11/6361973203003100007315109.png) 代表迭代的方向。松弛因子?籽表示迭代的步長。?籽的選擇十分重要。同一個算法只改變?籽的值,迭代收斂的速度變化如圖1所示。
代表迭代的方向。松弛因子?籽表示迭代的步長。?籽的選擇十分重要。同一個算法只改變?籽的值,迭代收斂的速度變化如圖1所示。
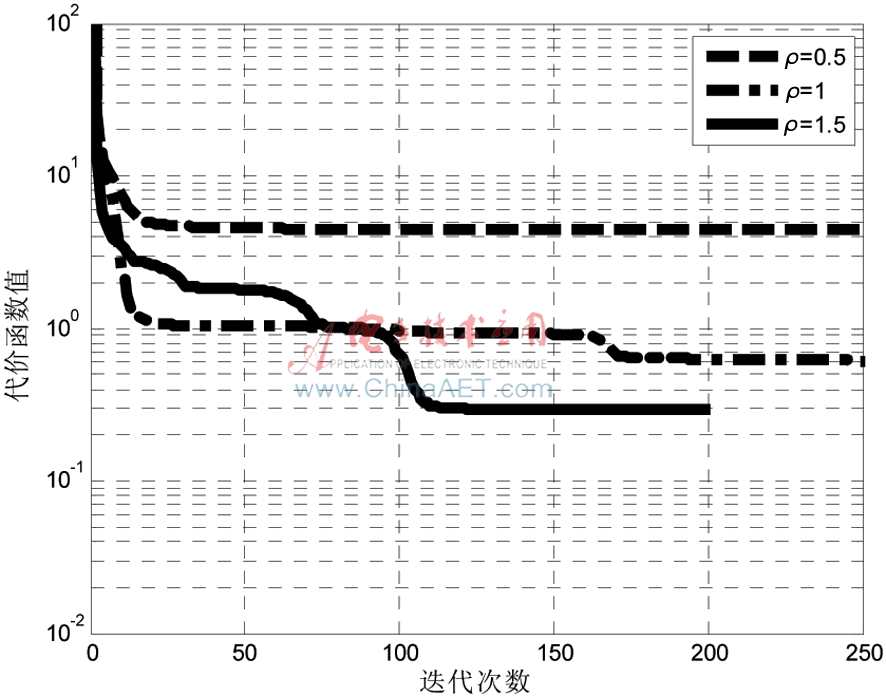
圖1 松弛因子?籽對迭代收縮的影響
2.3 平行因子的增強(qiáng)加權(quán)目標(biāo)函數(shù)
平行因子分解模型同獨立分量分析模型一樣,具有置換不確定性和排列不確定性。為了有效地解決這個問題而不犧牲算法的收斂性,本文采用如下收斂函數(shù):![1$@YGOESBUYOH~0U0L`]R[G.png 1$@YGOESBUYOH~0U0L`]R[G.png](http://files.chinaaet.com/images/2017/01/11/6361973210138100009786548.png)
其中 隨著迭代次數(shù)的增加?著趨于0。I表示與XJK×I相同維數(shù)的單位矩陣。式(15)可以寫為:
隨著迭代次數(shù)的增加?著趨于0。I表示與XJK×I相同維數(shù)的單位矩陣。式(15)可以寫為: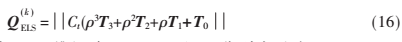
其中JK×I維矩陣T3、T2、T1和T0分別表示為:![EKN]56~OW0CEAQ1)C9MWY)T.png EKN]56~OW0CEAQ1)C9MWY)T.png](http://files.chinaaet.com/images/2017/01/11/6361973224782900005675876.png)
上標(biāo)k和k-2為了簡便已省略。定義Vec為矩陣矢量化符號,例如有矩陣A∈CI×J,則:![QP1]O8TPS5{G@O_H2O2PZ0L.png QP1]O8TPS5{G@O_H2O2PZ0L.png](http://files.chinaaet.com/images/2017/01/11/6361973228942300002239262.png)
則等式(16)等效于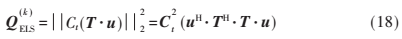
其中4×1維矢量![`M`YJ]SP8M3Z95)RK@@~34L.png `M`YJ]SP8M3Z95)RK@@~34L.png](http://files.chinaaet.com/images/2017/01/11/6361973239807000006698411.png) 代表共軛轉(zhuǎn)置,式(18)對于復(fù)數(shù)和實數(shù)都適用[7]。IJK×4維矩陣T分別由T3、T2、T1和T0的列矢量組合而成,可以表示為:
代表共軛轉(zhuǎn)置,式(18)對于復(fù)數(shù)和實數(shù)都適用[7]。IJK×4維矩陣T分別由T3、T2、T1和T0的列矢量組合而成,可以表示為:
3 數(shù)據(jù)實驗:分離混合語音的混合矩陣
本節(jié)通過數(shù)值仿真實驗對本文算法(SO-WALS-ELS)與SOBIUM算法的性能做比較。混合矩陣估計的相對誤差公式為:
其中,![U$9(NK]AHEE5Z_F747H]C[3.png U$9(NK]AHEE5Z_F747H]C[3.png](http://files.chinaaet.com/images/2017/01/11/6361973617379000003331161.png) 。假設(shè)它們的列向量均已單位化且消除了排列順序的不確定性。
。假設(shè)它們的列向量均已單位化且消除了排列順序的不確定性。
實驗中采用4路獨立源信號混合成3路觀測信號為例,4路語音從語音庫中隨機(jī)選取,采樣率為16 kHz,取160 000點,混合方式為瞬時混合,H為混合矩陣。圖2為源信號,圖3為混合信號,圖4為分離信號,圖5為本文算法與SOBIUM算法的對比圖。
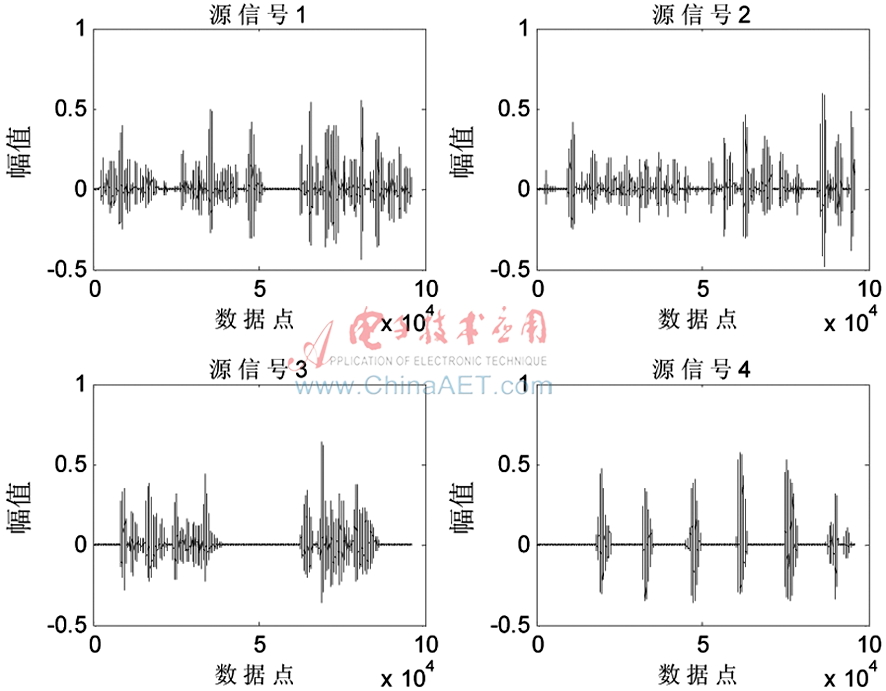
圖2 源信號

圖3 混合信號

圖4 分離信號
從圖2~圖5可以看出,改進(jìn)的算法分離出了大概原始信號,但分離信號的順序和極性都發(fā)生了變化,這也是目前平行因子分解尚無法解決的問題。![``(V6D5~UPJ}NY]5Y5UPI10.png ``(V6D5~UPJ}NY]5Y5UPI10.png](http://files.chinaaet.com/images/2017/01/11/6361973627631100001718278.png)
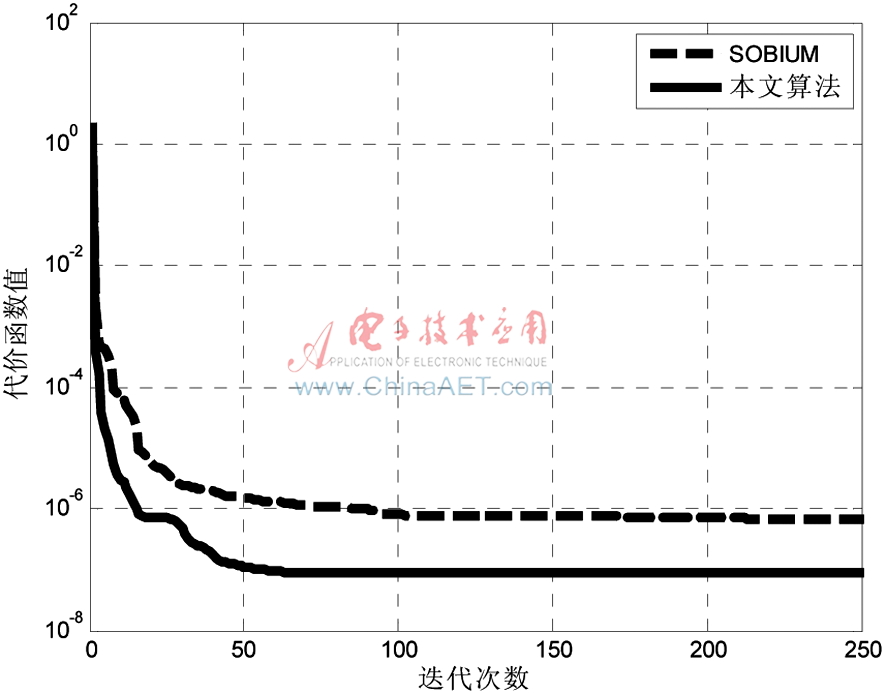
圖5 本文算法與SOBIUM算法的對比圖
![RG_M7DFZ8$2VM3{CP@]EKWF.png RG_M7DFZ8$2VM3{CP@]EKWF.png](http://files.chinaaet.com/images/2017/01/11/6361973631380400001348155.png)
根據(jù)公式,改進(jìn)前的算法相對誤差為0.055 9,改進(jìn)后的相對誤差為0.029 8。經(jīng)過多次實驗,改進(jìn)后的方法比原方法具有更快的收斂速度,并且更精確。
4 結(jié)論
本文提出了一種基于增強(qiáng)加權(quán)最小二乘法的欠定混合矩陣分離的新算法,適用于非平穩(wěn)信號。首先,該算法將接收信號的空間協(xié)方差矩陣疊加成三階張量,然后再對此三階張量進(jìn)行平行因子分解,最后利用增強(qiáng)加權(quán)最小二乘法完成混合矩陣估計。仿真實驗結(jié)果表明:本文提出的算法具有比SOBIUM算法更好的分離效果和更好的魯棒性,而且實現(xiàn)簡單,可滿足實際應(yīng)用的要求。
參考文獻(xiàn)
[1] LIEVEN De LATHAUWER.Blind identification of underde-termined mixtures by simultaneous matrix diagonalization[J].IEEE Transactions on Signal Processing,2008,56(3):1096-1105.
[2] PETR Tichavsky,ZBYNEK Koldovsky.Weight adjusted tensor method for blind separation of underdetermined mixtures of nonstationary sources[J].IEEE Transactions on Signal Processing,2011,59:1037-1047.
[3] KRUSKAL J B.Three-way arrays:Rank and uniqueness of trilinear decompositions,with application to arithmetic complexity and statistics,Linear Algebra Appl.,1977(18):95-138.
[4] STEGEMAN A,SIDIROPOULOS N D.On kruskal’s uniqueness condition for the Candecomp/ PARAFAC decomposition[C].Linear Algebra and its Applications,2007
(420):540-552.
[5] NICHOLAS D.SIDIROPOULOS,RASMUSBRO.On the Uni-queness of Multilinear Decomposition of N-way Arrays[J].J.Chemometrics,2000,14(3):229-239.
[6] RAJIH M,COMON P,HARSHMAN R A.Enhanced line search:A novel method to accelerate PARAFAC[J].SIAM Journal on Matrix Analysis,2008,30(3):1148-1171.
[7] NION D,DE LATHAUWER L.Line Search computation of the Block Factor Model for blind multi-user access in wireless communications[C].Advances in Wireless Communi-cations(SPAWC) France,Cannes,.IEEE Workshop on Signal Processing,2006.
[8] NION D,DE LATHAUWER I.An enhanced line Search scheme for complex-valued tensor decompositions.Application in DS-CDMA[J].Signal Processing,2008,3(88):749-755.

