文獻(xiàn)標(biāo)識碼: A
DOI:10.16157/j.issn.0258-7998.2015.11.025
中文引用格式: 梁溪,龍翔林,章恩友,等. 基于競爭機(jī)制的LDPC碼串行最小和算法[J].電子技術(shù)應(yīng)用,2015,41(11):89-92,100.
英文引用格式: Liang Xi,Long Xianglin,Zhang Enyou,et al. A serial min-sum algorithm for LDPC codes based on competitive scheme[J].Application of Electronic Technique,2015,41(11):89-92,100.
0 引言
隨著信息化的發(fā)展,人們對低密度奇偶校驗(yàn)(Low Density Parity Check,LDPC)碼有了重新的認(rèn)識。LDPC碼作為高效的信道糾錯(cuò)編碼,具有較低的譯碼復(fù)雜度,系統(tǒng)吞吐量較大,已在電力線載波(Power Line Carrier,PLC)通信、第三代和第四代無線移動(dòng)通信等方面得到了廣泛應(yīng)用[1]。相對于turbo譯碼算法[2],采用LDPC編碼和置信傳播(Belief Propagation,BP)譯碼算法更受人們的青睞[3]。但是BP算法存在對硬件存儲量的需求較大以及對信道情況較為敏感等問題。人們更趨向于魯棒性更好和復(fù)雜度更低的譯碼算法,最典型的就是并行最小和(Parallel Min-Sum,PMS)算法[4]。這類算法在實(shí)現(xiàn)中只需要加法和比較運(yùn)算,且不需要知道信道情況,可以獲得性能和復(fù)雜度的良好折衷。考慮到PMS算法前后兩次迭代譯碼過程中,參與信息交換的置信度被過高估計(jì),文獻(xiàn)[5]通過引入歸一化權(quán)重因子來減少這種負(fù)面影響,使其性能逼近最優(yōu)BP算法的性能,可稱之為歸一化并行最小和(Normalized Parallel Min-Sum,N-PMS)算法。隨著研究的深入,人們提出了不同的譯碼機(jī)制來提高置信傳播的效率,其中較為重要的一類是采用權(quán)重因子的串行最小和(Normalized Serial Min-Sum,N-SMS)算法[6]。在電力線載波通信中,收發(fā)模塊通常采用具有低存儲量和低復(fù)雜度的編、譯碼算法。N-SMS算法雖然在存儲上較N-PMS算法有一定減少,但N-SMS算法由于每次迭代都采用min操作來更新最小值,復(fù)雜度相對較高。
為實(shí)現(xiàn)可靠通信,并綜合考慮實(shí)現(xiàn)成本、器件功耗以及處理復(fù)雜度的問題,針對N-SMS算法提出了一種基于競爭機(jī)制的歸一化的串行最小和(Normalized Competitive Min-Sum,N-CMS)算法。該算法在按照自然順序更新變量節(jié)點(diǎn)對校驗(yàn)節(jié)點(diǎn)消息的同時(shí),還利用競爭關(guān)系更新變量節(jié)點(diǎn)對校驗(yàn)節(jié)點(diǎn)消息集合中的最小值。與文獻(xiàn)[6]類似的是,N-CMS在更新某一變量節(jié)點(diǎn)時(shí),同時(shí)利用了與該節(jié)點(diǎn)之前已更新的軟信息和該節(jié)點(diǎn)之后還未更新的軟信息,所以N-SMS算法與N-CMS算法的性能相同。不同的是,N-CMS通過采用競爭機(jī)制來更新屬于同一校驗(yàn)式的變量節(jié)點(diǎn)集合中的最小值,避免了文獻(xiàn)[6]中采用min操作的復(fù)雜運(yùn)算,并進(jìn)一步減少了存儲量。
1 N-PMS算法簡介
為了簡化敘述,該文沿用文獻(xiàn)[7]中的部分符號定義。設(shè)m和n分別表示校驗(yàn)節(jié)點(diǎn)和變量節(jié)點(diǎn),H為LDPC碼對應(yīng)的校驗(yàn)矩陣,當(dāng)變量節(jié)點(diǎn)和校驗(yàn)節(jié)點(diǎn)有邊相連接時(shí),則hmn=1,它是H中的第m行和n列的元素。N(m)={n|hmn=1}表示參與校驗(yàn)方程m的變量節(jié)點(diǎn)的集合,N(m)\n為N(m)中除去元素n后構(gòu)成的集合;相應(yīng)地,M(n)={m|hmn=1}表示與變量節(jié)點(diǎn)n相連的校驗(yàn)節(jié)點(diǎn)的集合,M(n)\m為集合M(n)中除去元素m后構(gòu)成的集合。設(shè)![26)IPLI]CR2JI[@1M7JC_S4.png 26)IPLI]CR2JI[@1M7JC_S4.png](http://files.chinaaet.com/images/2017/01/12/6361982660851053851171961.png) 是從變量節(jié)點(diǎn)n傳遞給校驗(yàn)節(jié)點(diǎn)m的軟信息,表示在給定接收序列y,并且除了第m個(gè)校驗(yàn)方程外,其他與n相關(guān)的校驗(yàn)方程都滿足的條件下,xn=x的概率;
是從變量節(jié)點(diǎn)n傳遞給校驗(yàn)節(jié)點(diǎn)m的軟信息,表示在給定接收序列y,并且除了第m個(gè)校驗(yàn)方程外,其他與n相關(guān)的校驗(yàn)方程都滿足的條件下,xn=x的概率;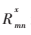 是由校驗(yàn)節(jié)點(diǎn)m傳遞給變量節(jié)點(diǎn)n的軟信息,表示在xn=x,且參加第m個(gè)校驗(yàn)方程的除n外的其他變量節(jié)點(diǎn)
是由校驗(yàn)節(jié)點(diǎn)m傳遞給變量節(jié)點(diǎn)n的軟信息,表示在xn=x,且參加第m個(gè)校驗(yàn)方程的除n外的其他變量節(jié)點(diǎn) 的概率Qmn已知的條件下,該校驗(yàn)方程成立的概率,其中
的概率Qmn已知的條件下,該校驗(yàn)方程成立的概率,其中 ∈N(m)\n。
∈N(m)\n。
設(shè)s為長為N的編碼序列x=[x1,x2,…,xN]T經(jīng)過BPSK調(diào)制后的信號,g是均值為0、方差為![HV[]OZ%0X@XAT0M4Z3UB6JF.png HV[]OZ%0X@XAT0M4Z3UB6JF.png](http://files.chinaaet.com/images/2017/01/12/6361982673620953857988851.png) 的高斯噪聲。設(shè)s經(jīng)過AWGN信道后的接收序列為y=[y1,y2,…,yN]T,BP譯碼后的序列為
的高斯噪聲。設(shè)s經(jīng)過AWGN信道后的接收序列為y=[y1,y2,…,yN]T,BP譯碼后的序列為![P%HB`7~L$P%YVJS3@]E$@EX.png P%HB`7~L$P%YVJS3@]E$@EX.png](http://files.chinaaet.com/images/2017/01/12/6361982674820453851559832.png) 。其中
。其中
![1S9Q8U5@KC4{JR9]APHB]~Y.png 1S9Q8U5@KC4{JR9]APHB]~Y.png](http://files.chinaaet.com/images/2017/01/12/6361982675601153858367176.png)
傳統(tǒng)的N-PMS算法可歸納如下:
初始化:令先驗(yàn)信息L(Pn)=yn,L(Qnm)=L(Pn)
步驟1:判斷是否達(dá)到設(shè)定的最大迭代次數(shù)MT,若是則程序結(jié)束;否則執(zhí)行步驟(2)。
步驟2:對m=1,2,…,M和所有的n∈N(m)計(jì)算:
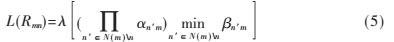
在上式中,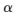 nm=sign(L(Qnm))和
nm=sign(L(Qnm))和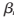 nm=abs(L(Qnm)),分別表示L(Qnm)的符號和絕對值,
nm=abs(L(Qnm)),分別表示L(Qnm)的符號和絕對值,![]%OZPKXTJ8X}R811CD)B75I.png ]%OZPKXTJ8X}R811CD)B75I.png](http://files.chinaaet.com/images/2017/01/12/6361982682270853854838095.png) 為歸一化權(quán)重因子,滿足0≤
為歸一化權(quán)重因子,滿足0≤![]%OZPKXTJ8X}R811CD)B75I.png ]%OZPKXTJ8X}R811CD)B75I.png](http://files.chinaaet.com/images/2017/01/12/6361982682682553855976389.png) ≤1。
≤1。
步驟3:對n=1,2,…,N和所有的m∈M(n)計(jì)算:
![Y9S55%}ZS88)OMZSI3]KQ%S.png Y9S55%}ZS88)OMZSI3]KQ%S.png](http://files.chinaaet.com/images/2017/01/12/6361982683921053859485236.png)
L(Qnm)=L(Qn)-L(Rmn)(7)
步驟4:對譯碼軟信息進(jìn)行硬判決,若L(Qn)<0,則![P%HB`7~L$P%YVJS3@]E$@EX.png P%HB`7~L$P%YVJS3@]E$@EX.png](http://files.chinaaet.com/images/2017/01/12/6361982685632453859623498.png) n=1,否則
n=1,否則![P%HB`7~L$P%YVJS3@]E$@EX.png P%HB`7~L$P%YVJS3@]E$@EX.png](http://files.chinaaet.com/images/2017/01/12/6361982686473053854788240.png) n=0,n=1,2,…,N。若H
n=0,n=1,2,…,N。若H![P%HB`7~L$P%YVJS3@]E$@EX.png P%HB`7~L$P%YVJS3@]E$@EX.png](http://files.chinaaet.com/images/2017/01/12/6361982688874153854208334.png) T=0,則譯碼成功,程序結(jié)束,否則轉(zhuǎn)到步驟(1)。
T=0,則譯碼成功,程序結(jié)束,否則轉(zhuǎn)到步驟(1)。
2 N-CMS算法的原理與實(shí)現(xiàn)步驟
在N-PMS中,校驗(yàn)節(jié)點(diǎn)和變量節(jié)點(diǎn)是分別并行更新的。文獻(xiàn)[4]指出,對于H矩陣中的第m個(gè)校驗(yàn)式,N-PMS在計(jì)算所有n∈N(m)集合中的最小值![M]B7]J{]Q5N72MRH8~~%0S4.png M]B7]J{]Q5N72MRH8~~%0S4.png](http://files.chinaaet.com/images/2017/01/12/6361982691770453852993720.png) 時(shí),可以通過找出該集合中最小的兩個(gè)量
時(shí),可以通過找出該集合中最小的兩個(gè)量![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982693506853851373096.png) 1和
1和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982693910653853015824.png) 2來簡化運(yùn)算。
2來簡化運(yùn)算。
基于文獻(xiàn)[4]的思想,設(shè)變量節(jié)點(diǎn)n更新前與更新后L(Qnm)的絕對值分別為 nm和
nm和![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982702455653856858088.png) ,
,![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982694377753853276462.png) 1和
1和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982695011253857577285.png) 2是集合n∈N(m)所有
2是集合n∈N(m)所有 nm中最小的兩個(gè)值,不失一般性令
nm中最小的兩個(gè)值,不失一般性令![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982695474553855928048.png) 1≤
1≤![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982695854853859849578.png) 2。當(dāng)
2。當(dāng)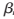 nm完成到
nm完成到![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982705695753857052079.png) 的更新后,使得n∈N(m)集合在
的更新后,使得n∈N(m)集合在 nm更新前求得的
nm更新前求得的![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982707412453857277207.png) 1和
1和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982707844253854185641.png) 2可能并不是當(dāng)前最小的兩個(gè)值,例如存在?茁
2可能并不是當(dāng)前最小的兩個(gè)值,例如存在?茁![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982708633953857494379.png) <
<![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982708985253858398543.png) 1的情況,此時(shí)的兩個(gè)最小值應(yīng)為
1的情況,此時(shí)的兩個(gè)最小值應(yīng)為![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982709755953858814577.png) 和
和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982710281253859948245.png) 1。倘若不對
1。倘若不對![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982757252053852353500.png) 1和
1和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982757714653853653131.png) 2進(jìn)行更新,則會(huì)導(dǎo)致
2進(jìn)行更新,則會(huì)導(dǎo)致![M]B7]J{]Q5N72MRH8~~%0S4.png M]B7]J{]Q5N72MRH8~~%0S4.png](http://files.chinaaet.com/images/2017/01/12/6361982711444753851738792.png) 的值不準(zhǔn)確,使得性能和收斂速率都會(huì)受到影響。但若要采用min操作來更新
的值不準(zhǔn)確,使得性能和收斂速率都會(huì)受到影響。但若要采用min操作來更新![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982715903753857029017.png) 1和
1和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982716531153856476624.png) 2,則計(jì)算復(fù)雜度會(huì)較高。如在文獻(xiàn)[6]中,對于碼率1/2的規(guī)則(N,J,2J)LDPC碼,N-SMS在每次迭代中,
2,則計(jì)算復(fù)雜度會(huì)較高。如在文獻(xiàn)[6]中,對于碼率1/2的規(guī)則(N,J,2J)LDPC碼,N-SMS在每次迭代中,![M]B7]J{]Q5N72MRH8~~%0S4.png M]B7]J{]Q5N72MRH8~~%0S4.png](http://files.chinaaet.com/images/2017/01/12/6361982713952853855977299.png) 操作需要NJ(2J+「log22J-2)次加法運(yùn)算,當(dāng)J較大時(shí),簡化N-SMS算法的復(fù)雜度是很有必要的。
操作需要NJ(2J+「log22J-2)次加法運(yùn)算,當(dāng)J較大時(shí),簡化N-SMS算法的復(fù)雜度是很有必要的。
![E@B({A)8__9C65S6]01U%1E.png E@B({A)8__9C65S6]01U%1E.png](http://files.chinaaet.com/images/2017/01/12/6361982718622553855419686.png)
步驟1:判斷是否達(dá)到設(shè)定的最大迭代次數(shù)MT,若是則程序結(jié)束;否則按照n=1,2,…,N的順序更新變量節(jié)點(diǎn)對校驗(yàn)節(jié)點(diǎn)的消息,執(zhí)行步驟(2)。
步驟2:對特定的n和每一個(gè)m∈M(n)按照式(5)計(jì)算L(Rmn),此處的min操作由![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982769948753854273565.png) 1和
1和![]%OZPKXTJ8X}R811CD)B75I.png ]%OZPKXTJ8X}R811CD)B75I.png](http://files.chinaaet.com/images/2017/01/12/6361982770489553854150520.png) 2取代。
2取代。
步驟3:對特定的n和每一個(gè)m∈M(n)依據(jù)式(6)、式(7)算出L(Qn)和L(Qnm),由更新后的L(Qnm)得出![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982721736653853948716.png) 后,再根據(jù)競爭模式更新
后,再根據(jù)競爭模式更新![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982751840953855939381.png) 1和
1和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982752294753855699016.png) 2。
2。
步驟4:若n≤N,對譯碼軟信息進(jìn)行硬判決,若L(Qn)<0,則![P%HB`7~L$P%YVJS3@]E$@EX.png P%HB`7~L$P%YVJS3@]E$@EX.png](http://files.chinaaet.com/images/2017/01/12/6361982723247653856843823.png) n=1,反之
n=1,反之![P%HB`7~L$P%YVJS3@]E$@EX.png P%HB`7~L$P%YVJS3@]E$@EX.png](http://files.chinaaet.com/images/2017/01/12/6361982723779153857636772.png) n=0,n=n+1轉(zhuǎn)到步驟(2)。否則執(zhí)行步驟(5)。
n=0,n=n+1轉(zhuǎn)到步驟(2)。否則執(zhí)行步驟(5)。
步驟5:若H![P%HB`7~L$P%YVJS3@]E$@EX.png P%HB`7~L$P%YVJS3@]E$@EX.png](http://files.chinaaet.com/images/2017/01/12/6361982724433853854422065.png) T=0,則譯碼成功,程序結(jié)束。否則轉(zhuǎn)到步驟(1)。
T=0,則譯碼成功,程序結(jié)束。否則轉(zhuǎn)到步驟(1)。
3 復(fù)雜度及存儲量分析


另一方面,N-PMS需要較大的存儲,根據(jù)式(5),對于每個(gè)校驗(yàn)式m,![M]B7]J{]Q5N72MRH8~~%0S4.png M]B7]J{]Q5N72MRH8~~%0S4.png](http://files.chinaaet.com/images/2017/01/12/6361982728930653857322904.png) 需要2個(gè)單元來存儲2個(gè)最小值,所以對于N/2個(gè)校驗(yàn)式,L(Rmn)總共需N個(gè)存儲單元;根據(jù)式(6)、式(7),L(Qn)、L(Qnm)分別需N和NJ個(gè)存儲單元。再來看N-SMS算法,由于變量節(jié)點(diǎn)串行更新,L(Rmn)只需2J個(gè)存儲,但N-SMS算法每次迭代都要進(jìn)行min操作,對于每個(gè)校驗(yàn)式m,L(Qnm)仍需2J個(gè)
需要2個(gè)單元來存儲2個(gè)最小值,所以對于N/2個(gè)校驗(yàn)式,L(Rmn)總共需N個(gè)存儲單元;根據(jù)式(6)、式(7),L(Qn)、L(Qnm)分別需N和NJ個(gè)存儲單元。再來看N-SMS算法,由于變量節(jié)點(diǎn)串行更新,L(Rmn)只需2J個(gè)存儲,但N-SMS算法每次迭代都要進(jìn)行min操作,對于每個(gè)校驗(yàn)式m,L(Qnm)仍需2J個(gè)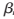 nm來計(jì)算
nm來計(jì)算![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982730581953854822252.png) ,從而L(Qn)、L(Qnm)分別仍需N和NJ個(gè)存儲單元。在N-CMS算法中,L(Rmn)也只需2J個(gè)存儲,由于N-CMS算法采用了競爭機(jī)制,每計(jì)算出一個(gè)
,從而L(Qn)、L(Qnm)分別仍需N和NJ個(gè)存儲單元。在N-CMS算法中,L(Rmn)也只需2J個(gè)存儲,由于N-CMS算法采用了競爭機(jī)制,每計(jì)算出一個(gè)![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982731943953858768767.png) ,便用于
,便用于![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982754883153854473189.png) 1和
1和![J_VAD@LY]R(5`$4WIW%[Q0M.png J_VAD@LY]R(5`$4WIW%[Q0M.png](http://files.chinaaet.com/images/2017/01/12/6361982755314553859933187.png) 2的更新。所以對于每個(gè)校驗(yàn)式m,只需分配1個(gè)臨時(shí)單元用于存儲
2的更新。所以對于每個(gè)校驗(yàn)式m,只需分配1個(gè)臨時(shí)單元用于存儲![}VKPU]]]1LI3[$DW]3X7KKJ.png }VKPU]]]1LI3[$DW]3X7KKJ.png](http://files.chinaaet.com/images/2017/01/12/6361982732377553858884232.png) ,從而L(Qnm)共需N/2個(gè)單元,L(Qn)需N個(gè)存儲單元。綜上所述,N-PMS、N-SMS和N-CMS所需存儲總量分別為2N+NJ、N+(N+2)J和3N/2+2J。顯而易見,相對于N-PMS算法和N-SMS算法,N-CMS算法具有極低的存儲需求,這對于設(shè)計(jì)成本低廉的譯碼模塊具有重要意義。
,從而L(Qnm)共需N/2個(gè)單元,L(Qn)需N個(gè)存儲單元。綜上所述,N-PMS、N-SMS和N-CMS所需存儲總量分別為2N+NJ、N+(N+2)J和3N/2+2J。顯而易見,相對于N-PMS算法和N-SMS算法,N-CMS算法具有極低的存儲需求,這對于設(shè)計(jì)成本低廉的譯碼模塊具有重要意義。
4 算法仿真與測試
仿真中選取碼率1/2的(512,3,6)規(guī)則LDPC碼通過AWGN信道,譯碼分別采用N-PMS算法和N-CMS算法。為了使得信息得到充分的傳播,在仿真中令最大迭代譯碼次數(shù)MT=30。下面從歸一化權(quán)重因子的選取、誤比特率(Bit Error Rate,BER)、誤幀率(Frame Error Rate,F(xiàn)ER)、收斂速率和譯碼平均譯碼復(fù)雜度幾個(gè)方面來進(jìn)行對比分析。
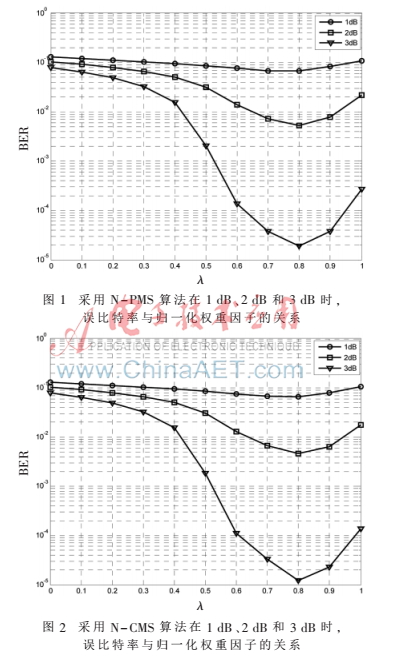
為簡化討論,此處利用蒙特卡羅方法來獲得N-PMS和N-CMS的歸一化權(quán)重因子。如圖1和圖2所示,兩者都在![]%OZPKXTJ8X}R811CD)B75I.png ]%OZPKXTJ8X}R811CD)B75I.png](http://files.chinaaet.com/images/2017/01/12/6361982737670953854738452.png) =0.8時(shí)表現(xiàn)出最佳的性能,因此將
=0.8時(shí)表現(xiàn)出最佳的性能,因此將![]%OZPKXTJ8X}R811CD)B75I.png ]%OZPKXTJ8X}R811CD)B75I.png](http://files.chinaaet.com/images/2017/01/12/6361982738001053857096666.png) =0.8作為最佳歸一化權(quán)重因子用于之后的仿真。
=0.8作為最佳歸一化權(quán)重因子用于之后的仿真。

圖3和圖4分別對比了PMS、N-PMS、CMS和N-CMS系統(tǒng)的BER和FER性能,按照是否引入歸一化權(quán)重因子分為兩組,即PMS和N-PMS,CMS和N-CMS。可以看出,不論哪一組歸一化算法均比非歸一化的算法性能要好得多,約有0.5~0.7 dB的性能差距。此外,即使都是歸一化算法,N-CMS較N-PMS也有0.1~0.2 dB的性能提升。


由圖5可知,CMS所需的平均迭代譯碼次數(shù)要少于PMS,類似的,N-CMS所需的平均迭代譯碼次數(shù)也少于N-PMS。從圖6可以得出,N-CMS在中低信噪比時(shí)譯碼復(fù)雜度較N-SMS有明顯的優(yōu)勢,但比N-PMS略高;在高信噪比時(shí)N-CMS與N-PMS復(fù)雜度接近,而且兩者都比N-SMS的復(fù)雜度低。
5 結(jié)論
本文提出了一種按照變量節(jié)點(diǎn)更新的歸一化串行最小和算法——N-CMS。N-CMS算法采用競爭機(jī)制實(shí)時(shí)更新變量節(jié)點(diǎn)對校驗(yàn)節(jié)點(diǎn)消息集合中最小的兩個(gè)值,它在保持與N-SMS算法相同性能的前提下大幅降低了運(yùn)算量。相對N-PMS算法而言,N-CMS算法不論是在收斂速度,還是在譯碼性能上都更有優(yōu)勢,其復(fù)雜度只有略微增加。最為重要的是N-CMS算法具有極低的存儲需求,尤其是在電力線載波通信所需的譯碼模塊的設(shè)計(jì)中,表現(xiàn)出巨大的實(shí)用價(jià)值。
參考文獻(xiàn)
[1] DEVELI I,KABALCI Y.Analysis of the use of different decoding schemes in LDPC coded OFDM systems over indoor PLC channel[J].Electronics & Electrical Engineering,2014,20(1):76-80.
[2] BERROU C,GLAVIEUX A,THITIMAJSHIMA P.Near Shannonlimit error-correcting coding:turbo codes[C].In ICC93,1993(5):1064-1070.
[3] MACKAY D J C.Good error-correcting codes based on very sparse matrice[J].IEEETrans.Inform.Theory,1999(45):399-431.
[4] FOSSORIER M P C,MIHALJEVIC M,IMAI H.Reduced complexity iterative decoding of low density parity check codes based on belief propagation[J].IEEE Trans.Commun,1999(47):673-680.
[5] CHEN J,F(xiàn)OSSORIER M P C.Decoding low-density parity check codes with normalized APP-based algorithm[C].Proc.IEEE Global Communications Conference,2001,9(1):1026-1030.
[6] 劉原華,王新梅,胡樹楷,等.一種改進(jìn)的卷積LDPC碼置信傳播譯碼算法[J].西安電子科技大學(xué)學(xué)報(bào),2009, 36(3):424-428.
[7] 楊帆,羅振東,田寶玉.改進(jìn)的LDPC串行譯碼[J].北京郵電大學(xué)學(xué)報(bào),2008,31(4):130-134.

