0 引言
    在無(wú)線(xiàn)通信系統(tǒng)中天線(xiàn)陣列可以用來(lái)提升系統(tǒng)容量和信號(hào)質(zhì)量，所以角度參數(shù)對(duì)天線(xiàn)陣列性能的影響很重要,。波達(dá)信號(hào)的角域包括水平方位到達(dá)角（Azimuth of Arrival,，AOA）和俯仰角（Elevation of Arrival，EOA）,。文獻(xiàn)[1]中研究包含三維(three Dimensional,，3D)天線(xiàn)陣列方法，假設(shè)方位到達(dá)角AOA在[0,，2π]上均勻分布,，仰角則是不均勻地分布在水平面上。文獻(xiàn)[1]中沒(méi)有給出與水平方位到達(dá)角AOA,、俯仰角EOA,、天線(xiàn)陣列幾何相關(guān)的閉合解析式。文獻(xiàn)[2]中研究表明大約65%的入射信號(hào)相對(duì)于水平方位角平面仰角大于10°,。文獻(xiàn)[3]中提到室內(nèi)到室外幾種環(huán)境中平均仰角擴(kuò)展為9°,。文獻(xiàn)[4]研究表明均勻線(xiàn)陣（Uniform Linear Array，ULA）和均勻圓陣（Uniform Circular Array,，UCA）下均勻分布和拉普拉斯分布的到達(dá)角概率分布函數(shù)和空間相關(guān)性函數(shù),，結(jié)果受限于方位平面。本文將研究方位到達(dá)角AOA和仰角EOA在均勻矩形陣列（Uniform Rectangular Array,，URA）下對(duì)空間相關(guān)性的影響,。
    本文介紹了定向信道模型和均勻矩形陣列導(dǎo)向矢量（Steer Vector，SV）,，推導(dǎo)出在3D均勻矩形陣列多種功率譜分布下空間衰落相關(guān)性的封閉形式表達(dá)式,，分析AOA、EOA,、方位角擴(kuò)展(Azimuth Spread,，AS)、俯仰角擴(kuò)展(Elevation Spread,，ES)及陣元間距對(duì)相關(guān)性的影響,。采用多重信號(hào)分類(lèi)（Multiple Signal Classification，MUSIC）算法對(duì)MIMO系統(tǒng)波達(dá)信號(hào)方向進(jìn)行空間譜估計(jì),，推導(dǎo)了多種天線(xiàn)陣列空間譜通用公式,。本文分析可以應(yīng)用于多輸入多輸出（Multiple Input Multiple Output,，MIMO）系統(tǒng)容量分析以及MIMO系統(tǒng)的波達(dá)信號(hào)方向（Direction of Arrival，DOA）估計(jì),。
1 多天線(xiàn)信道模型
    使用非頻率選擇性瑞利衰落信道模型分析天線(xiàn)陣列性能,。信道脈沖響應(yīng)表示為[5]：

圖1  均勻線(xiàn)性陣列URA三維空間接收模型

2 均勻矩形陣列空間衰落相關(guān)性
    下面討論在天線(xiàn)陣列為3D均勻矩形陣列時(shí)，均勻分布和高斯分布情況下的空間相關(guān)性,。在均勻矩形陣列URA下,，(n，p)和(m,，q)兩陣元之間空間相關(guān)性表示為：

2.1 均勻分布情況下空間衰落相關(guān)性
    假設(shè)波達(dá)信號(hào)水平方位角AOA和俯仰角EOA是均勻角能量分布函數(shù),。其函數(shù)表達(dá)式為：

2.2 高斯分布情況下空間衰落相關(guān)性
    假設(shè)波達(dá)信號(hào)水平方位角AOA和俯仰角EOA遵循高斯角能量分布[7]。其函數(shù)表達(dá)式為：

3 波達(dá)信號(hào)空間譜分析
    空間譜是陣列信號(hào)處理中的重要概念,，是信號(hào)在空間各個(gè)方向上的能量分布,。本文利用MUSIC算法來(lái)分析URA下入射信號(hào)空間譜與其他天線(xiàn)陣列比較情況。MUSIC算法是利用接收數(shù)據(jù)協(xié)方差矩陣分離信號(hào)子空間和噪聲子空間,，通過(guò)正交性來(lái)構(gòu)成空間掃描譜估計(jì)參數(shù),。假設(shè)有n信號(hào)入射到陣元數(shù)為p的天線(xiàn)陣列，n≤p,，則其接收信號(hào)表達(dá)式為：

    式中，U_s是由大特征值對(duì)應(yīng)的特征矢量張成的子空間也即信號(hào)子空間,，而U_n是由小特征值對(duì)應(yīng)的特征矢量張成的子空間也即噪聲子空間,。假設(shè)信號(hào)子空間與噪聲子空間正交，且波達(dá)信號(hào)為弱相關(guān)或不相關(guān),，通過(guò)MUSIC算法得到空間譜公式為[8]：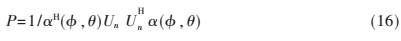

4 數(shù)值結(jié)果與分析

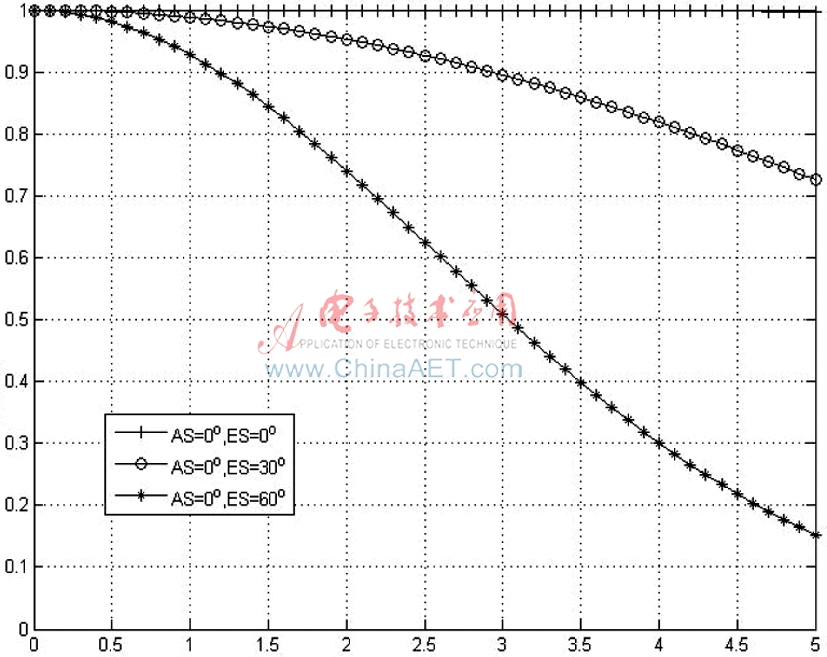
圖2  均勻分布下AS=0°時(shí)d/λ和ES對(duì)空間衰落相關(guān)性的影響

    圖2為入射信號(hào)遵循均勻分布時(shí),，俯仰角EOA和陣元間距對(duì)陣元(1，1)和陣元(2,，2)之間空間相關(guān)性的影響,。設(shè)定，AS為定值時(shí),，取ES為不同值,，比較兩個(gè)陣元之間相關(guān)性對(duì)于陣元間距的變化。隨著ES的增大,，兩陣元間相關(guān)性隨之減小,，隨著陣元間距的增大，空間相關(guān)性減小,。

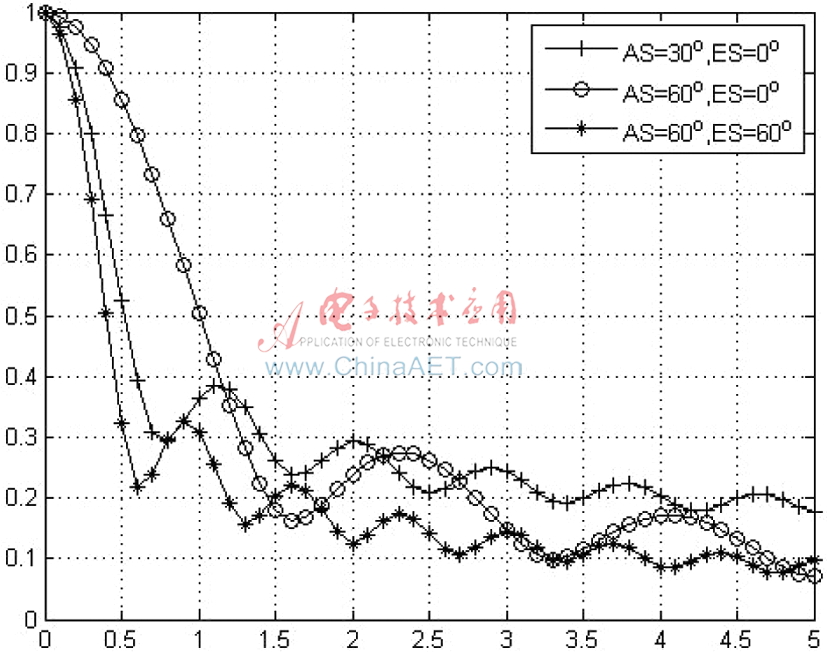
圖3  均勻分布下ES=0°時(shí)d/λ和AS對(duì)空間衰落相關(guān)性的影響

    圖3所示為方位到達(dá)角AOA和陣元間距對(duì)兩陣元間空間相關(guān)性的影響,。設(shè)定取90°，ES為定值時(shí),，取AS為不同值,，比較兩個(gè)陣元之間的相關(guān)性相對(duì)于陣元間距的變化,。從圖中可以明顯看出，隨著AS的增大,，兩陣元之間的相關(guān)性隨之減小,，同樣隨著陣元間距的增大，空間相關(guān)性減小,。

圖4  高斯分布下AS=0°時(shí)d/λ和ES對(duì)空間衰落相關(guān)性的影響

    圖4所示為入射信號(hào)遵循高斯分布時(shí),，方位到達(dá)角AOA和陣元間距對(duì)兩陣元間空間相關(guān)性的影響。當(dāng)AS為0°時(shí),，取ES為不同值,，比較兩個(gè)陣元之間的相關(guān)性相對(duì)于陣元間距的變化。從圖中可以看出隨著ES的增加空間相關(guān)性減小,。

圖5  高斯分布下ES=0°時(shí)d/λ和ES對(duì)空間衰落相關(guān)性的影響

    如圖5所示,，入射信號(hào)遵循高斯分布時(shí)，方位到達(dá)角AOA和陣元間距對(duì)兩陣元之間的空間相關(guān)性的影響,。當(dāng)ES為0°時(shí),，取AS為不同值，可以看出隨著AS的增加,，空間衰落相關(guān)性下降的更快,，結(jié)論與均勻分布情況下得出的結(jié)論一致。

圖6  均勻線(xiàn)性陣列下空間譜

圖7  均勻圓形陣列下空間譜

圖8  均勻矩形陣列下空間譜

    如圖6～圖8所示為MIMO天線(xiàn)陣列在分別采用ULA,、UCA和URA情況下的空間譜分析仿真結(jié)果,。假設(shè)有9個(gè)天線(xiàn)陣元，ULA陣元間距為d=0.5λ,，UCA陣元半徑r=0.5λ,，URA陣元間距為d_x=d_y=0.5λ。在到達(dá)角參數(shù)Ф和θ取相同值的情況下,，入射信號(hào)在三維空間中進(jìn)行定位時(shí),，會(huì)出現(xiàn)相位模糊情況。圖6所示ULA空間為非均勻性,，方向選擇性強(qiáng),，所以波達(dá)信號(hào)的相位模糊比較嚴(yán)重，出現(xiàn)許多的MUSIC偽譜峰值,。在圖7和圖8中可以看出,，UCA和URA情況下相位模糊情況比ULA減弱，在θ角測(cè)向時(shí)可能出現(xiàn)一個(gè)偽譜峰值,。所以分析空間譜時(shí)采用UCA和URA會(huì)得到更好的效果,，趨向于無(wú)模糊定位。
5 結(jié)論
    本文推導(dǎo)了三維多徑信道中均勻矩形陣列URA在多種角能量分布下的空間衰落相關(guān)性解析公式,，分析AOA,、EOA,、AS、ES以及陣元間距對(duì)空間衰落相關(guān)性的影響,。采用多重信號(hào)分類(lèi)MUSIC算法對(duì)MIMO系統(tǒng)波達(dá)信號(hào)方向進(jìn)行空間譜估計(jì),，推導(dǎo)了多種天線(xiàn)陣列空間譜通用公式。通過(guò)計(jì)算機(jī)程序模擬仿真驗(yàn)證了分析結(jié)果,，仿真結(jié)果表明方位角擴(kuò)展AS和仰角擴(kuò)展ES是天線(xiàn)相關(guān)性的主要決定因素,，空間衰落相關(guān)性隨著AS和ES的增加而減小。當(dāng)AS和ES增加同樣角度時(shí),，在AS增加的情況下,，空間衰落相關(guān)性下降的更快，表明了AS對(duì)空間相關(guān)性影響更大,。仿真結(jié)果還表明,，采用同樣的參數(shù)情況下估計(jì)MIMO系統(tǒng)空間譜，均勻矩形陣列URA相對(duì)于ULA和UCA更有優(yōu)勢(shì),。
參考文獻(xiàn)
[1] AULIN T.A modified model for the fading signal at a mobile radio channel[J].Vehicular Technology,，IEEE Trans-actions on，1979,，28(3)：182-203.
[2] KUCHAR A,，ROSSI J P，BONEK E.Directional macro-cell channel characterization from urban measurements[J].Anten-nas and Propagation,，IEEE Transactions on,，2000，48(2)：137-146.
[3] KALLIOLA K,，SULONEN K，LAITINEN H,，et al.Angular power distribution and mean effective gain of mobile antenna in different propagation environ ments[J].Vehicular Technology,，IEEE Transactions on，2002,，51(5)：823-838.
[4] TSAI J A,，BUEHRER R M，WOERNER B D.Spatial fading correlation function of circular antenna arrays with Laplacian energy distribution[J].IEEE Communications Letters,，2002,，6
(5)：178-180.[5] 周杰，陳靖峰,，邱琳.三維空間MIMO信道接收天線(xiàn)陣列互耦效應(yīng)及系統(tǒng)容量分析[J].通信學(xué)報(bào),，2012，33(6)：1-10.
[6] YONG S K,，THOMPSON J S.Three-dimensional spatial fading correlation models for compact MIMO receivers[J].Wireless Communications,，IEEE Transactions on,，2005，4(6)：2856-2869.
[7] ZHOU J,，SASAKI S,，MURAMATSU S．Spatial correlation functions for a circular antenna array and their applications in wireless communication system[J]．IEICE  Trans FUNDAM COMPUT SCI，2003,，E86-A(7)：1716-1723.
[8] SALIB F,，SEDDIK K G.Exploiting spatial spectrum holes in multiuser MIMO systems[C].Signals, Systems and Com-puters，2013 Asilomar Conference on.IEEE,，2013：1865-1868.