0 引言

　　無線通信系統(tǒng)中天線陣列（Antenna Arrays，AAs）的選擇對信道容量和信號質(zhì)量的提高有著重要的意義,。由于天線陣列的性能主要基于多徑信道空間特性的開發(fā),，因此提高角度參數(shù)對于天線陣列性能影響的認知勢在必行。前人已針對到達方位角（Azimuth of Arrival,，AOA）概率密度函數(shù)（Probability Density Functions,，PDFs）在均勻分布或者拉普拉斯分布下的均勻天線陣列（Uniform Antenna Arrays，UAA）的空間衰落相關(guān)性（Spatial Fading Correlation,，SFC）進行研究并取得珍貴的成果[1-2],。由于現(xiàn)今移動通信設(shè)備的隨身特性，要求手持設(shè)備天線處于任意隨機的空間位置上都可以獲得良好的信號,，因此只考慮到達方位角的二維天線陣列模型有所局限[3],。在此基礎(chǔ)上，進一步考慮綜合到達方位角和到達仰角共同影響的三維環(huán)境下角度參數(shù)對于天線陣列的空間衰落相關(guān)性的影響有著重要的意義,。

　　在多輸入多輸出（Multiple Input Multiple Output,，MIMO）技術(shù)中，多天線被應(yīng)用于基站（Base Station,，BS）和移動站（Mobile Station,，MS）中是為高效利用空間信道的多徑分量。信道容量隨天線陣元個數(shù)的增加而線性增大,，但是陣元間距的減小同時會導(dǎo)致增大陣元間相關(guān)性,，甚至受到互耦效應(yīng)的影響[4]。一種獲得良好性能的方式是有效地隔離BS、MS天線單元以獲得較大的分集階數(shù),。在BS引入多天線并沒有明顯的技術(shù)難度,，但是在MS引入多天線卻難以實現(xiàn)。因此,，本文介紹了均勻矩形陣列（Uniform Rectangular Array,，URA）和電磁矢量傳感器（Electromagnetic Vector Sensor，EVS）天線陣列兩種小型天線陣（Compact Antenna Array CAA）模型,，其中EVS陣列是替代URA等傳統(tǒng)標(biāo)量傳感器陣列（Scalar Sensor Array,，SSA）的優(yōu)良選擇。

　　如圖1所示,，單點EVS模型由3個正交的電偶極子和3個正交的磁偶極子供電配置而成,，其偶極子和磁環(huán)尺寸均小于半個波長，同時可感應(yīng)電磁信號的3個時分電場分量和相應(yīng)的3個磁場分量具有同點極化分集接收能力,。EVS已被廣泛用于雷達,、聲吶等定向應(yīng)用方面。由于其具有的極化多樣性較傳統(tǒng)的雙極化系統(tǒng)能夠帶來更大的信道容量,，因而在移動通信系統(tǒng)中亦有著良好的應(yīng)用前景,。EVS具有緊湊的結(jié)構(gòu)，故可在一個天線陣列中配置多個EVS以獲得更好的性能,。MIMO信道容量與各天線單元間的SFC密切相關(guān),，所以研究小型天線陣中各陣元間的SFC有著重要的意義。

　　本文的研究目的是嘗試建立不同小型天線陣模型的相關(guān)性方程,，確立MIMO系統(tǒng)發(fā)射和接收兩端的相關(guān)性協(xié)方差矩陣,，以改善無線信道的性能；同時深入分析平均到達方位角（Mean Azimuth of Arrival,，MAOA）,、方位角擴展（Azimuth Spread，AS）,、平均到達仰角（Mean Elevation of Arrival,，MEOA）和方位角擴展（Elevation Spread，ES）等不同的角度參數(shù)對于SFC的影響,，研究系統(tǒng)性能對于不同參數(shù)的敏感性,；最后分析采用不同天線陣列模型的MIMO多天線系統(tǒng)的信道容量，以直觀表征不同天線陣列條件下的系統(tǒng)性能,。

1 三維信道模型

　　本文針對定向頻率非選擇性瑞利衰落信道模型進行性能分析,。利用多個不同時延的信道的線性疊加進行MIMO信道建模，其信道脈沖響應(yīng)表達式可為[5]：

　　其中,，j(t)為零均值的復(fù)獨立同分布隨機變量,，a(j)為天線陣列的導(dǎo)向矢量（Steering Vector,，SV）；JMPC為發(fā)射端天線總數(shù),；[θ,，φ，γ,，η]T為空間矢量參數(shù),，其中0≤φ＜2π、0≤θ＜π分別為方位角和仰角,，0≤γ＜π/2,、-π≤η＜π分別表示輔助極化角和極化相位差。假設(shè)URA中的天線單元為垂直極化的,，則只與φ和θ取值有關(guān),。因此，對于參考相位位于xoy平面原點的N×M個陣元的URA,，其導(dǎo)向矢量方程為：

　　對于EVS，其導(dǎo)向矢量方程為[6]：

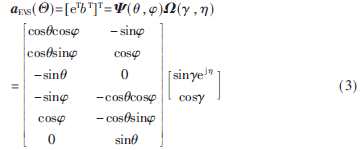
　　最后,，對于引入EVS的陣列,，其聯(lián)合導(dǎo)向矢量為：

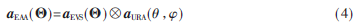
　　其中，kronecker乘積,，aEAA和aURA分別為實際情況下EVS和URA的導(dǎo)向矢量,。

2 空間衰落相關(guān)性

　　對于URA，陣元m和陣元n之間的SFC方程定義為[6-7]：

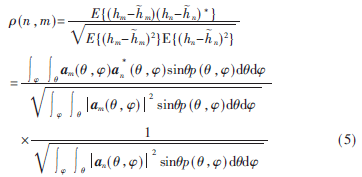
　　其中E[·]表示期望,，(·)?鄢表示復(fù)共軛,，hm表示陣元m信道脈沖響應(yīng)（即接收信號能量）均值，an(θ,，φ)為陣元n的導(dǎo)向矢量,，p(θ，φ)為多徑分量AOA聯(lián)合概率密度函數(shù),。在此假設(shè)天線數(shù)量足夠多,，故式(5)中的連續(xù)模型可以良好地近似式(1)中的離散模型。另假設(shè)AOA與EOA相互獨立,，則p(θ,，φ)可分解為p(θ)p(φ)。AOA在[φ0-Δφ,，φ0+Δφ]范圍內(nèi)均勻分布[1],，其中Δφ和φ0分別為AS和MAOA。同樣,，EOA在[θ0-Δθ,，θ0+Δθ]范圍內(nèi)均勻分布，其中Δθ和θ0分別為ES和MEOA。

　　在天線的每點陣元上配置EVS構(gòu)成小型天線陣列,，考慮包括極化域在內(nèi),，則式(5)將轉(zhuǎn)變?yōu)槿缦率絒8]：

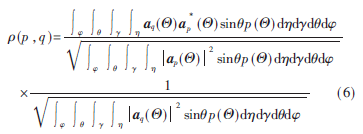
　　假設(shè)p分別為在[0，π/2]和在[-π,，π]上均勻分布,，故可推導(dǎo)出陣元m所接收入射信號的第p空間極化分量與陣元n所接收入射信號的第q空間極化分量之間的SFC的閉合表達式：

　　其中：

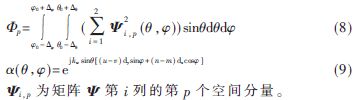
3 MIMO天線陣列信道容量

　　在對無線信道容量評估中，通常MIMO多徑衰落信號信道容量作為衡量包含信道鏈接端點的信道質(zhì)量的一種方式,。如果在接收端已知多徑信道信息,，而發(fā)送端未知時，可在發(fā)送端假設(shè)信道矩陣服從零均值空間白噪聲模型,。為使信道遍歷容量最大化,，最優(yōu)的策略是將功率平均分配到每個發(fā)送天線上，即遍歷容量最大化的輸入?yún)f(xié)方差矩陣為Rx=(MBS)I,。因此,，遍歷容量可表示為：

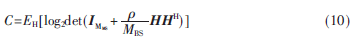
　　其中，MBS和MMS分別為BS和MS的天線陣元數(shù)量,；I為MMS階單位矩陣,；傳輸信號的信噪比（SNR）；H=RHw(R)T為MIMO多天線信道矩陣[9],，RMS是MS多天線陣元間衰落信號相關(guān)矩陣,，RBS是BS多天線陣元間衰落信號相關(guān)矩陣，Hw是具有相同分布的復(fù)高斯隨機矩陣,，表示矩陣的轉(zhuǎn)置,。由于在系統(tǒng)級的天線設(shè)計中基站的天線陣列形式一般不能任意選擇，考慮理想的垂直極化非相關(guān)天線陣列,，將基站相關(guān)矩陣RBS表示為RBS=I,。(·)H表示共軛轉(zhuǎn)置，EH(·)為求數(shù)學(xué)期望以對信道矩陣H的分布進行均值分析,。

4 仿真結(jié)果與分析

　　此節(jié)將對天線陣列的空間衰落相關(guān)性和所構(gòu)成MIMO系統(tǒng)的信道容量進行仿真模擬,，驗證所得結(jié)果與理論推導(dǎo)的結(jié)論是否符合，直觀顯示不同的天線陣列模型對于系統(tǒng)性能的影響,。此處仿真均假設(shè)AOA和EOA的概率密度函數(shù)均符合均勻分布,，MS多天線陣列包含6×6個陣元。

　　4.1 空間衰落相關(guān)性

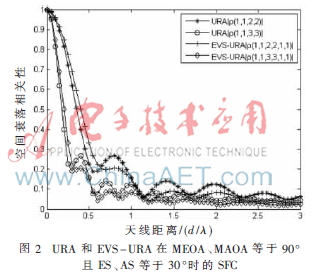
　　圖2給出天線陣列在MAOA和MEOA等于90°,、AS和ES等于30°時空間衰落相關(guān)性與天線距離間的關(guān)系,。對比陣元1、3與陣元1,、2的曲線,可以看出由于陣元間距增大會加速SFC的衰落,；EVS陣列相比SSA陣列衰落系數(shù)幅度更低,，并且波動更小，說明EVS陣列能夠有效抑制多徑信道相關(guān)特性,，并因此改善系統(tǒng)性能,。

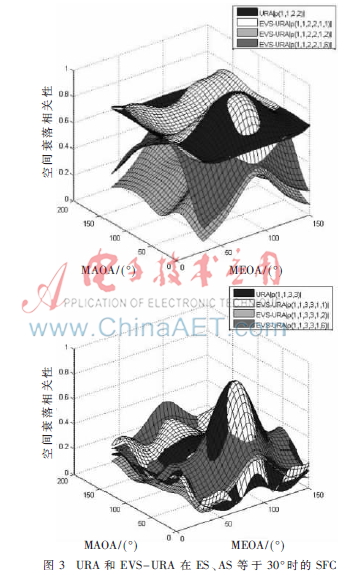
　　圖3給出天線陣列在d/λ等于0.5，AS和ES等于30°時空間衰落相關(guān)性與MAOA和MEOA的關(guān)系,，其中EVS陣列取空間極化分量1,、2、6,，并將對應(yīng)天線陣元 (a,，b)間的SFC表示為ρ(a，b,，1,，1)、ρ(a,，b,，1，2)和ρ(a,，b,，1，6),。

　　由圖中可以看出陣列的相關(guān)性曲面均關(guān)于仰角θ=90°左右對稱，且在90°處達到最大,；方位角φ的變化對于相關(guān)性的影響比θ更大,。引入EVS后，除了ρ(a,，b,，1，1)與ρ(a,，b)近似,，其他空間極化分量組合在相關(guān)性上有著明顯的不同，且均帶來相關(guān)特性的顯著改善,。

　　4.2 信道容量

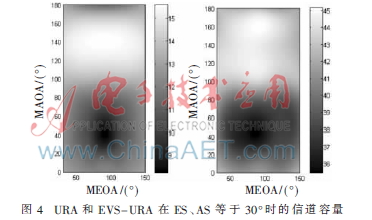
　　圖4給出在d/λ等于0.5,、AS和ES等于30°時信道容量與MAOA和MEOA的關(guān)系。由圖可以看出,，URA陣列信道容量關(guān)于φ,、θ均呈對稱趨勢，并在對稱中心容量達到最大,；在θ為0或者180°附近,，信道容量基本不受φ變化的影響,。EVS陣列相比SSA陣列均增加了約3倍的信道容量，極大地優(yōu)化了系統(tǒng)的性能,。綜上表明,，EVS陣列性能明顯優(yōu)于SSA陣列。

5 結(jié)語

　　本文建立了URA小型天線陣列模型,，并將EVS單元與其相結(jié)合,，推導(dǎo)出空間衰落相關(guān)性的表達式，并利用相關(guān)矩陣計算出信道容量,。最后通過一系列的仿真模擬,，得到了與理論推導(dǎo)符合的結(jié)果。天線陣元數(shù)量的增加能夠有效提高MIMO系統(tǒng)的性能,，但是陣元間的相關(guān)性和互耦效應(yīng)以及空間極化效應(yīng)則會導(dǎo)致信道容量的下降,。采用EVS的天線陣列能夠有效緩解多徑信道的相關(guān)特性，從而使信道容量顯著增加,，因此EVS天線陣列具有優(yōu)異的性能和良好的應(yīng)用前景,。

參考文獻

　　[1] SALZ J，WINTERS J H.Effect of fading correlation on adaptive arrays in digital mobile radio[J].IEEE Transactionson Vehicular Technology,，1994,，43(4)：1049-1057.

　　[2] TSAI J A，BUEHRER R B,，WOERNER B D.Spatial fadingcorrelation function of circular antenna arrays with laplaciandistribution energy[J].IEEE Communication Letters,，2002，6(5)：178-180.

　　[3] EGGERS P C F,，KOVACS I Z,，OLESEN K.Penetration effects on XPD with GSM 1800 handset antennas，relevant for BS polarization diversity for indoor coverage[C].VehicularTechnology Conference,，1998.VTC 98.48th IEEE.IEEE,，1998，3：1959-1963.

　　[4] FOSCHINI G J,，GANS M J.On limits of wireless commun-in a fading environment when using multiple antennas[J].Wireless Personal Communications,，1998，6(3)：311-335.

　　[5] IOANNIDES P,，BALANIS C.Uniform circular and rectang-ular arrays for adaptive beamforming applications[J].Antennasand Wireless Propagation Letters,，IEEE，2005,，4：351-354.

　　[6] YONG S K,，THOMPSON J S.Three dimensional spatial fading correlation models for compact MIMO receivers[J].IEEE Transactions on Communications，2005,，4(6)：2856-2869.

　　[7] ZHOU J,，SASAKI S,，MURAMATSU S，et al.Spatial correlationfor a circular antenna array and its applications in wireless communication[C].Global Telecommunications Conference,，2003.GLOBECOM′03,，IEEE.IEEE，2003,，2：1108-1113.

　　[8] YONG S K,，THOMPSON J S.A 3-Dimensional spatial fadingcorrelation model for electromagnetic vector sensors[A].IEEE International Symposium on Antennas，Propagation andEM Theory[C].Beijing,，China,，2003：843-847.