0 引言

    基于信道信息的物理層認證利用了豐富的無線信道資源,，以信道為“指紋”特征，是一種對傳統(tǒng)認證技術(shù)的有效補充和增強^[1,，2],，但是物理層認證在時變情況下受到挑戰(zhàn)。本文討論時變信道中連續(xù)數(shù)據(jù)幀的認證,，當前后兩個數(shù)據(jù)幀的時間間隔小于信道的“相干時間”,，同時非法攻擊者與合法發(fā)送者之間的距離大于傳輸波長的一半的情形下進行。傳統(tǒng)的結(jié)合最小二乘（Least Square,，LS）和二元假設(shè)檢驗的物理層認證利用了無線信道響應(yīng)的時空唯一性^[3],，但是由于利用LS方法進行信道探測時不考慮可分徑的各個抽樣值的相關(guān)性，無法準確跟蹤時變信道的時變特性,。本文提出采用基擴展模型（Basis Expansion Model,，BEM）作為信道探測的方法，其特點在于將可分徑的各個抽樣值在塊傳輸時間內(nèi)存在相關(guān)性作為一種資源,，用于補充和增強移動通信的接入安全認證機制,。

1 系統(tǒng)模型

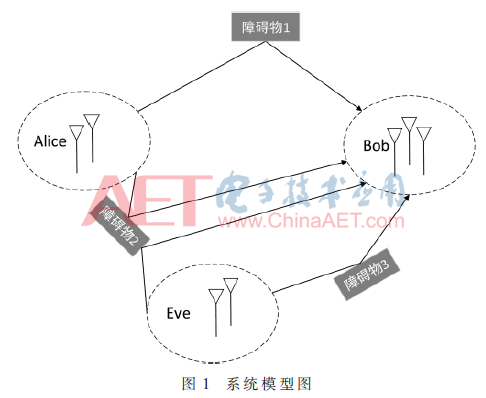
    本文的認證涉及到3種不同的身份，分別是：合法發(fā)送者Alice,、合法接收者Bob,，以及企圖偽冒Alice來欺騙Bob的非法發(fā)送者Eve。如圖1所示,，Alice和Eve發(fā)送的信號經(jīng)歷不同的路徑到達接收端Bob處,，Bob通過物理層認證區(qū)分這些不同，從而判斷消息是否合法,。

    在OFDM系統(tǒng)中,，OFDM符號是傳輸?shù)幕締卧１疚男诺澜Ｒ彩窃谝粋€OFDM符號中展開的,，設(shè)信道多徑數(shù)為L,，子載波數(shù)為N。BEM模型擬合時變信道,，實質(zhì)上是擬合時域信道的沖擊響應(yīng),。第l個信道抽頭在n時刻的信道沖擊響應(yīng)為h(n,，l)，BEM模型采用相互正交的基函數(shù)和不變的基系數(shù)來逼近該狀態(tài)^[4],，表示為：

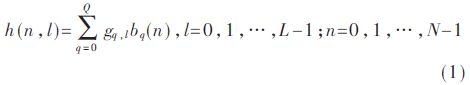
式中：Q為BEM模型的階數(shù),；g_q，l為第l個信道抽頭的第q個基系數(shù),，保持不變,；b_q(n)為第q個基函數(shù)，不同的BEM模型產(chǎn)生不同的基函數(shù),。

1.1 復(fù)指數(shù)BEM模型

    復(fù)指數(shù)基擴展模型(Complex Exponential BEM,，CE-BEM)是最常見的模型，采用傅里葉基作為基函數(shù),，即：

其中,，ω_q＝2π(q-Q/2)/N。采用Q階復(fù)指數(shù)BEM模型對信道建模時,，采用了多普勒譜的Q+1個分量,，誤差較大，容易導(dǎo)致頻譜泄露,，引起吉布斯效應(yīng),。文獻[5]將其改進為過采樣CE-BE(Oversampling CE-BEM，OCE-BEM)將周期設(shè)為CE-BEM的p倍,，避免頻譜泄露現(xiàn)象,。

1.2 多項式BEM模型

    多項式BEM模型（Polynomial BEM，P-BEM）采用泰勒級數(shù)展開得到的多項式的線性組合來擬合信道,，基函數(shù)為：

    P-BEM對多普勒擴展敏感,，僅適用于低多普勒擴展的情況。

1.3 離散卡-洛BEM模型

    離散卡-洛BEM模型(Discrete Karhunen-Loeve BEM,，DKL-BEM)在均方誤差準則下最優(yōu),。但是，適用DKL-BEM的前提是必須已知信道的相關(guān)矩陣,，并且信道的多功率譜滿足特定的形狀,。

1.4 離散長橢球序列BEM模型

    離散長橢球序列BEM模型(Discrete Prolate Spheroidal BEM，DPS-BEM)適用于所有的信道類型,。它采用矩形功率譜構(gòu)成階方陣,，再經(jīng)計算得到基函數(shù),。

1.5 基模型選取

    經(jīng)以上分析,，CE-BEM模型誤差大，容易導(dǎo)致頻譜泄露,；P-BEM模型對多普勒擴展敏感,；DKL-BEM模型必須已知信道的相關(guān)矩陣,，并且要求信道的多功率譜滿足特定的形狀，實際認證中無法滿足該條件,；DPS-BEM模型計算較為復(fù)雜,。本文中考慮可行性和高效性，選取OCE-BEM模型來擬合無線認證環(huán)境中的時變信道,。

2 二元假設(shè)檢驗統(tǒng)計量

    時變信道中,，在滿足物理層認證條件的前提下，Bob對發(fā)送的連續(xù)消息可以通過二元假設(shè)檢驗^[6]來實現(xiàn)認證,。

    當“差值”小于“閾值”時,，信道矩陣很相似，判定當前發(fā)送者為Alice,；當“差值”大于“閾值”時,，信道矩陣不相似，判定當前發(fā)送者為Eve,。由此可見,，“差值”的計算和“閾值”的選取是物理層認證的關(guān)鍵。

2.1 改進的歸一化LRT方法

    計算“差值”需要先選定檢驗統(tǒng)計量,，信道響應(yīng)的幅度差和相位差是最常用的檢驗統(tǒng)計量,。由于基于幅度的檢驗統(tǒng)計量和基于幅度和相位的統(tǒng)計檢驗量均含有未知的噪聲功率σ²，無法直接計算“絕對差值”,。改進的歸一化似然比檢驗（Likelihood Ratio Test,，LRT）方法使用連續(xù)3個數(shù)據(jù)幀（前兩幀已認證，第3幀待認證）,，求“相對差值”,，消除了噪聲功率σ²。改進的歸一化LRT統(tǒng)計量為：

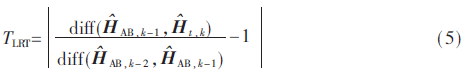
2.2 基于幅度的改進的歸一化LRT統(tǒng)計量

    基于幅度的改進歸一化LRT統(tǒng)計量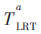考慮信道響應(yīng)的幅度差,，可得：

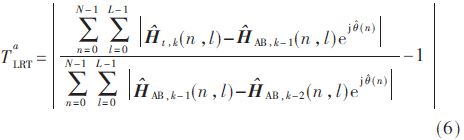
2.3 基于幅度和相位的改進歸一化LRT統(tǒng)計量

    基于幅度和相位的改進歸一化LRT統(tǒng)計量考慮信道響應(yīng)的幅度差和相位差,，可得：

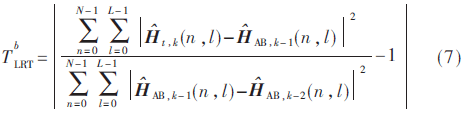
3 仿真實驗

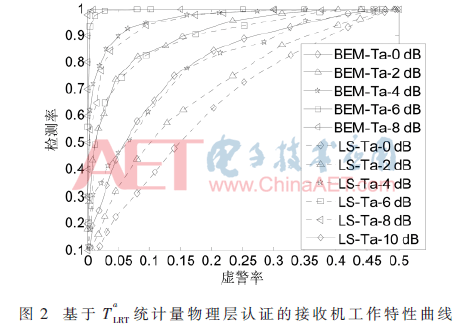
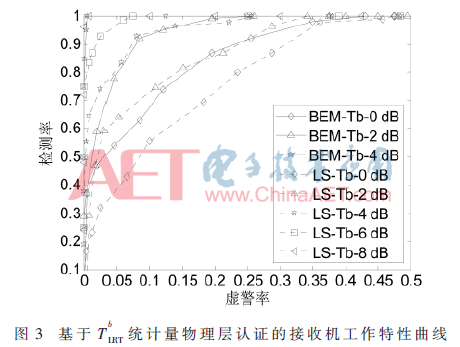
    本文采用Jakes模型產(chǎn)生瑞利信道，信道多徑數(shù)為6,，采樣間隔為5 μs,，子載波數(shù)為256，循環(huán)前綴長度為30,，載波頻率為2 GHz,，智能終端速度為40 km/h?；贐EM信道估計的導(dǎo)頻開銷為7/32(一個導(dǎo)頻簇長度為7),，基于LS信道估計的導(dǎo)頻開銷為1/4(導(dǎo)頻間隔為3)，近似認為二者導(dǎo)頻開銷相等,。設(shè)定BEM和LS信道估計的其他仿真條件均相同,，分別在基于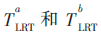統(tǒng)計量情況下,，“閾值”選取(0，3),，仿真1 000次,。圖2和圖3分別為基于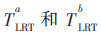統(tǒng)計量的物理層認證中接收機Bob的工作特性曲線。

4 結(jié)論

    本文提出基于基擴展模型的物理層認證方法,，通過在OFDM系統(tǒng)中進行的仿真實驗,，證明該認證方法的有效性，且相對于傳統(tǒng)的LS信道探測的物理層認證,，獲得2～4 dB性能提升,。性能提升的原因主要是信道探測準確率提高，原因有二：(1)基于BEM信道估計的導(dǎo)頻簇中兩側(cè)為保護導(dǎo)頻,，降低了時變子載波間干擾的影響,，非零導(dǎo)頻處的信道估計準確率更高；(2)基于BEM信道估計考慮了各個抽樣值在塊傳輸時間內(nèi)存在相關(guān)性,，比“插值”更準確地跟蹤信道變化,，從而使數(shù)據(jù)處信道估計準確度高。

參考文獻

[1] XIAO L,，GREENSTEIN L,，MANDAYAM N，et al.Finger-prints in the ether：Using the physical layer for wireless authentication[C].IEEE International Conference on Communications(ICC′07),，2007：4646-4651.

[2] WEN H,，WANG Y，ZHU X,，et al.Physical layer assist authentication technique for smart meter system[J].IET Communications,，2013，7(3)：189-197.

[3] MA T,，JIANG Y,，WEN H，et al.Physical layer assist mutual authentication scheme for smart meter system[C].IEEE Conference on Communications and Network Security(CNS 2014),，2014：494-495.

[4] 李昕.基于基擴展快時變信道模型的OFDM系統(tǒng)信道估計[D].成都：西南交通大學(xué),，2013.

[5] LEUS G.On the estimation of rapidly time varying channels[C].EUSIPCO 2004，Vienna,，Austria,，2004：2227-2230.

[6] 胡細寶，孫洪祥,，王麗霞.概率論·數(shù)理統(tǒng)計·隨機過程[M].北京：北京郵電大學(xué)出版社,，2007.

[7] 馬婷.智能電網(wǎng)中的輕量級物理層輔助認證技術(shù)研究[D].成都：電子科技大學(xué)，2015.