《電子技術(shù)應(yīng)用》
您所在的位置：首頁 > 嵌入式技術(shù) > 設(shè)計(jì)應(yīng)用 > 一種可實(shí)現(xiàn)的仿射組合自適應(yīng)濾波算法
一種可實(shí)現(xiàn)的仿射組合自適應(yīng)濾波算法
2014年電子技術(shù)應(yīng)用第5期
郭業(yè)才1,2， 張冰龍2， 吳彬彬2
1. 南京信息工程大學(xué) 江蘇省氣象探測(cè)與信息處理重點(diǎn)實(shí)驗(yàn)室, 江蘇 南京210044;2. 南京信息工程大學(xué) 電子與信息工程學(xué)院, 江蘇 南京 210044
摘要： 為了進(jìn)一步改善自適應(yīng)算法收斂速度和穩(wěn)態(tài)偏差的性能，在對(duì)仿射組合濾波器自適應(yīng)算法性能分析的基礎(chǔ)上，提出了一種新的組合參數(shù)更新公式,，該更新公式中的固定系數(shù)改為與子濾波器輸出相關(guān)的函數(shù),，使仿射組合自適應(yīng)濾波算法可以更好地實(shí)時(shí)跟蹤子濾波器的性能變化。仿真結(jié)果表明,，基于新組合參數(shù)更新公式的仿射組合自適應(yīng)濾波算法與基于理想組合參數(shù)更新公式的仿射組合自適應(yīng)濾波算法性能一致,，同時(shí)具有快的收斂速度和低的穩(wěn)態(tài)偏差，且對(duì)子濾波器步長變化具有良好的跟蹤性能,。
中圖分類號(hào)： TN911.6
文獻(xiàn)標(biāo)識(shí)碼： A
文章編號(hào)： 0258-7998(2014)05-0108-03
A realizable affine combination of adaptive filtering algorithm
Guo Yecai1,2, Zhang Binglong2, Wu Binbin2
1. Jiangsu Key Laboratory of Meteorological Observation and Information Processing, Nanjing University of Information Science & Technology, Nanjing 210044, China;2.School of Electronic＆Information Engineering, Nanjing University of Information Science＆Technology, Nanjing 210044,China
Abstract： In order to further improve the performance of convergence rate and steady deviation of the adaptive algorithm, this paper proposed a new combination parameter updating formula based on the analysis of performance on affine combination adaptive filters. In this proposed updating formula, the fixed coefficient is replaced with the function associated with the sub-filters output, which can make the affine combination adaptive filtering algorithm track the performance of sub-filters in real-time. Simulation results show that the performance of the affine combination adaptive filtering algorithm based on the proposed updating formula of the combination parameter is consistent with that of the affine combination adaptive filtering algorithm based on the ideal updating formula of the combination parameter, has fast convergence speed and low steady-state deviation, and can track the variable step-size of sub-filters.
Key words : adaptive algorithm; affine combination; combination parameter; convergence speed; steady-state deviation

　　在自適應(yīng)算法的設(shè)計(jì)中,，收斂速度和穩(wěn)態(tài)誤差是兩個(gè)重要的指標(biāo)，然而在一般的自適應(yīng)算法設(shè)計(jì)中,，這兩個(gè)指標(biāo)往往不能同時(shí)達(dá)到最佳值,，即收斂速度快、穩(wěn)態(tài)誤差大,，而收斂速度慢,、穩(wěn)態(tài)誤差小[1]。為了獲得收斂速度快,、穩(wěn)態(tài)誤差小的自適應(yīng)算法,，研究人員提出了自適應(yīng)濾波算法的凸組合方案[2-5]，它的優(yōu)點(diǎn)在于組成結(jié)構(gòu)相對(duì)簡(jiǎn)單,，并且在穩(wěn)態(tài)和非穩(wěn)態(tài)情況下均有良好的性能[6],。

　　最近，自適應(yīng)仿射組合算法被提出[7],，它是凸組合算法的推廣,。在凸組合算法中，采用sigmoid函數(shù)作為組合參數(shù)?姿(n),，因此?姿(n)的取值范圍是[0,1],；而對(duì)于仿射組合算法，組合參數(shù)?姿(n)的取值不受區(qū)間[0,1]的限制,，它的取值在穩(wěn)態(tài)下為負(fù)值[8],。組合參數(shù)?姿(n)是仿射組合算法中重要的控制因子，通過對(duì)組合參數(shù)的調(diào)整,，可以實(shí)現(xiàn)對(duì)每個(gè)子濾波器的切換,。從理論上說，該仿射組合算法可以獲得每個(gè)子自適應(yīng)濾波算法的優(yōu)點(diǎn),，即同時(shí)具有快的收斂速度和小的穩(wěn)態(tài)誤差,。

　　本文分析了仿射組合自適應(yīng)濾波算法的瞬態(tài)過程和穩(wěn)態(tài)過程，并提出了一種可實(shí)現(xiàn)的更新組合參數(shù)的方法,。仿真結(jié)果表明,，該組合參數(shù)的性能曲線同時(shí)具有快的收斂速度和低的穩(wěn)態(tài)誤差，與最佳性能曲線一致,。

1 仿射組合自適應(yīng)濾波算法

　　仿射組合自適應(yīng)濾波算法原理框圖如圖1所示,。

001.jpg

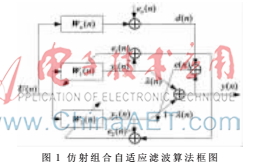
　　圖1中,，每個(gè)濾波器均采用LMS算法，濾波器1采用的LMS算法,，步長為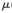%EM3_$K8JHQR8FQ9[QQ@J[U.jpg1,；濾波器2采用的LMS算法。

　　LMS自適應(yīng)算法濾波器權(quán)向量Wi(n)更新公式為:

　　68EB9HJEX%[G~2JKK6U3NSR.png

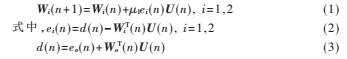
　　其中,，W1(n)是濾波器1的N階權(quán)向量,，W2(n)是濾波器2的N階權(quán)向量。假設(shè)eo(n)是均值為0,、方差為的噪聲信號(hào),，并且和其他信號(hào)統(tǒng)計(jì)獨(dú)立,。U(n)為輸入信號(hào),，U(n)=[u(n),…,u(n-N+1)]T。

　　組合后的輸出信號(hào)為：

　　LJJIH6_N`TG[3)6T{$[J`9O.png

　　式(10)表明,，當(dāng)系統(tǒng)處于穩(wěn)態(tài)時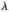(shí),，7E1L1I(9GP66LW8[6ATLIZO.pngo(n)<0。

　　由于兩個(gè)子濾波器對(duì)最佳權(quán)向量的估計(jì)有一定的相關(guān)性,，因此在穩(wěn)態(tài)時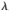(shí),，7E1L1I(9GP66LW8[6ATLIZO.png(n)<0表明采用子濾波器1估計(jì)系統(tǒng)最優(yōu)權(quán)向量值應(yīng)當(dāng)減去用子濾波器2估計(jì)系統(tǒng)最優(yōu)權(quán)向量的值，從而避免噪聲信號(hào)及兩個(gè)子濾波器對(duì)最佳權(quán)向量估計(jì)的相關(guān)性所帶來的誤差干擾[9],。

2 歸一化組合參數(shù)?姿(n)的更新公式

　　由于式(9)是在理想情況下得出的,，在實(shí)際應(yīng)用中難以實(shí)現(xiàn)，因此本文提出一種可實(shí)現(xiàn)的歸一化組合參數(shù)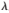7E1L1I(9GP66LW8[6ATLIZO.png(n)的更新公式,。

　　對(duì)E[e2(n)|W2(n),W12(n)]求偏導(dǎo)并使它等于0,，可得:

　　7P[VI%7UGB~FQUO7SZZ}~_C.png

　　式(12)是組合參數(shù)?姿(n)的一階隨機(jī)時(shí)變遞歸表達(dá)式。式(12)較穩(wěn)定,，但是跟蹤子濾波器的性能較差,；若N]3]4]TTD39~E$SC4TCO%FM.jpg>1時(shí)，系統(tǒng)的跟蹤性能較好,，但是容易導(dǎo)致式(12)的初始階段調(diào)整的不穩(wěn)定,。因此這里采用類似于NLMS算法形式的功率歸一化方案調(diào)整參數(shù)，在初始階段小于1,，以保持系統(tǒng)的穩(wěn)定性,；在過渡階段及穩(wěn)態(tài)階段大于1，以保證系統(tǒng)對(duì)子濾波器具有較好的跟蹤性能,。令:

　　~4}BRDIGIBSY0E1(TCJ$LXY.png

3 仿真分析

　　假設(shè)未知系統(tǒng)為7階FIR濾波器模型,，自適應(yīng)濾波器的階次與未知模型階次相同,并且每次仿真均采用100次蒙特卡洛循環(huán),方差為1的高斯白噪聲信號(hào)。這里采用均方偏差MSD(Mean Square Deviation)表征仿射組合算法的性能,。

002.jpg

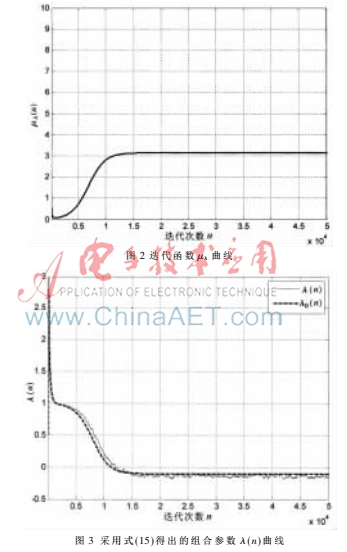
　　圖2 給出了迭代函數(shù)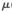%EM3_$K8JHQR8FQ9[QQ@J[U.jpg(n)曲線,。圖3給出了仿射組合濾波算法組合參數(shù)N]3]4]TTD39~E$SC4TCO%FM.jpg(n)曲線,。圖3中虛線表示由式(9)得出的最佳組合參數(shù)N]3]4]TTD39~E$SC4TCO%FM.jpgo(n)的曲線，實(shí)線表示采用式(15)得到的曲線,。圖3表明,，本文所提出的組合參數(shù)N]3]4]TTD39~E$SC4TCO%FM.jpg(n)的曲線和最優(yōu)組合參數(shù)N]3]4]TTD39~E$SC4TCO%FM.jpg(n)的曲線幾乎一致，在穩(wěn)態(tài)時(shí),，組合參數(shù)的值小于零,。

003.jpg

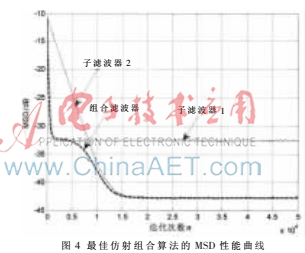
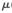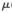　　圖4展示了在理想情況下仿射組合自適應(yīng)濾波算法的均方偏差性能曲線。圖4中收斂較快的曲線是濾波器1的收斂曲線,，收斂較慢的曲線是濾波器2的收斂曲線,，由于%EM3_$K8JHQR8FQ9[QQ@J[U.jpg1>%EM3_$K8JHQR8FQ9[QQ@J[U.jpg2，濾波器1的收斂速度比濾波器2的收斂速度快,。虛線表示根據(jù)理論推導(dǎo)所得出的理想組合算法的均方誤差曲線,。

004.jpg

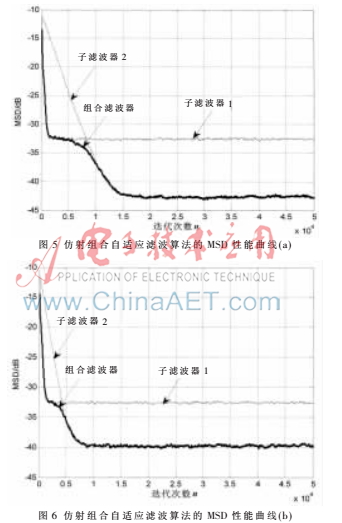
　　圖5和圖6展示了采用式(15)作為組合參數(shù)得出的仿射組合濾波算法穩(wěn)態(tài)偏差性能曲線。兩個(gè)組成濾波器的步長是固定的,，圖5中的濾波器1的步長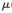%EM3_$K8JHQR8FQ9[QQ@J[U.jpg1=0.1,，濾波器2的步長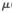%EM3_$K8JHQR8FQ9[QQ@J[U.jpg2=0.02。圖6中的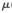%EM3_$K8JHQR8FQ9[QQ@J[U.jpg1=0.1, 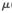%EM3_$K8JHQR8FQ9[QQ@J[U.jpg2=0.03,。從圖5和圖6可以看出,，組合后的均方偏差MSDc隨著濾波器1和濾波器2的均方偏差變化而變化。在初始階段,，組合濾波器的性能曲線跟隨濾波器1的性能曲線,；在過渡階段，組合濾波器的性能曲線逐漸由濾波器1過渡到濾波器2,；穩(wěn)態(tài)階段,，組合濾波器的性能曲線跟隨濾波器2的性能曲線，改變組成濾波算法的步長值,，組合后的算法性能曲線仍然具有良好的跟蹤性能,。

　　仿射組合自適應(yīng)濾波算法是凸組合算法的推廣，仿射組合自適應(yīng)濾波算法的組合參數(shù)N]3]4]TTD39~E$SC4TCO%FM.jpg(n)不受區(qū)間[0,1]的限制,。在仿射組合算法中,，每個(gè)子濾波器對(duì)未知信道產(chǎn)生獨(dú)立的估計(jì)，因此存在一個(gè)最佳仿射組合系數(shù)使穩(wěn)態(tài)偏差最小,。本文對(duì)兩個(gè)自適應(yīng)濾波器組成的仿射組合自適應(yīng)濾波算法的性能進(jìn)行了分析研究,，提出了一個(gè)可實(shí)現(xiàn)的組合參數(shù)N]3]4]TTD39~E$SC4TCO%FM.jpg(n)的更新公式，并得出了相應(yīng)的仿真結(jié)果,。仿真結(jié)果表明,，本文提出的組合參數(shù)更新公式與最佳組合參數(shù)更新公式一致，采用該組合參數(shù)的仿射組合算法可以實(shí)現(xiàn)自適應(yīng)算法快的收斂速度和低的穩(wěn)態(tài)偏差,，對(duì)信號(hào)處理領(lǐng)域研究具有一定的參考價(jià)值,。

　　參考文獻(xiàn)

　　[1] 張愛民,， 王星全. 自適應(yīng)陣列智能天線抗干擾性能研究[J].電子技術(shù)應(yīng)用,2012,38(1):94-96.

　　[2] 于霞，劉建昌,，李鴻儒.一種變步長凸組合自適應(yīng)濾波器及其均方性能分析[J].電子學(xué)報(bào),，2010,38(2):480-484.

　　[3] 芮國勝，苗俊,，張洋,等.基于凸組合的同步長最大均方權(quán)值偏差自適應(yīng)濾波算法[J].通信學(xué)報(bào),，2012,33(3):28-34.

　　[4] SILVA M T M, ARENAS G J. A soft-switching blindequalization scheme via convex combination of adaptive fil-ters[J].IEEE Transactions on Signal Processing,2013,61(5):1171-1182.

　　[5] NASCIMENTO V H, de LAMARE R C. A low-complexitystrategyfor speeding up the convergence of convex combina-tions ofadaptive filters[C].IEEE International Conference onAcoustics, Speech and Signal Processing.Kyoto,2012:3553-3556.

　　[6] SANG-WOOK S, JEONGKYU L,KYEONG-PYO L,et al.Subband adaptive convex combination of two NLMS basedfilters for sparse impulse response systems[C].IEEE Statisti-cal Signal Processing Workshop (SSP), Ann Arbor,2012:201-204.

　　[7] RAJIB L D, BIJIT K D, MRITYUNJOY C. Improve theper Formance of the LMS algorithm via cooperative learning[C]. National Conference Communication(NCC),New Delhi,2013:1-5.

　　[8] KALEEM A M, TAMBOLI A I. An affine combination oftwo time varying LMS adaptive filters[C].International Con-ference on Communication,Information&Computing Technolo-

gy(ICCICT),Mumbai,India,2012:1-4.

　　[9] BERSHAD N J, BERMUDEZ J C M, TOURNERET J Y.An affine combination of two LMS adaptive filters-Tran-sient mean-square analysis[J]. IEEE Transactions on SignalProcessing,2008,56(5):1853-1864.


此內(nèi)容為AET網(wǎng)站原創(chuàng)，未經(jīng)授權(quán)禁止轉(zhuǎn)載,。