0 引言

　　傳統(tǒng)的奈奎斯特采樣定理要求采樣率高于信號(hào)最高頻率的兩倍,，來實(shí)現(xiàn)信號(hào)的采集,、壓縮和恢復(fù)。但隨著采集數(shù)據(jù)和頻率的急劇增加,，壓縮過程中丟棄了絕大部分采集數(shù)據(jù),，只保留了小部分來恢復(fù)信號(hào)，導(dǎo)致增加大量不必要的存儲(chǔ)和傳輸設(shè)備,。Donoho,、Candès等人提出的壓縮感知理論很好地解決了這個(gè)難題[1-2]。壓縮感知將可稀疏的信號(hào)通過觀測從高階矩陣線性投影為低階,，信號(hào)的采集和壓縮在此過程同時(shí)進(jìn)行,，最后高概率精確地重建原始信號(hào)。在語音信號(hào)的處理過程中,，模擬信號(hào)的高采樣率必然會(huì)產(chǎn)生海量的冗余數(shù)據(jù),，根據(jù)語音信號(hào)的可壓縮性，DCT變換域以及小波變換的稀疏特性,，滿足壓縮感知理論的先驗(yàn)條件[3-4],。壓縮感知的理論包含三項(xiàng)內(nèi)容：選擇信號(hào)稀疏基，設(shè)計(jì)觀測矩陣和重構(gòu)原信號(hào),。其中信號(hào)是否具有稀疏性是前提條件,；設(shè)計(jì)觀測矩陣是實(shí)現(xiàn)的重要部分,，不僅關(guān)系到壓縮和采樣速率的快慢，而且影響重構(gòu)信號(hào)的質(zhì)量,；重構(gòu)原始信號(hào)是壓縮感知理論的核心,，決定著恢復(fù)原信號(hào)質(zhì)量的好壞。

1 語音自適應(yīng)壓縮感知的設(shè)計(jì)

　　信號(hào)在稀疏矩陣變換下越稀疏,，重構(gòu)時(shí)所用的觀測數(shù)目就越少,，重建信號(hào)的效率就越高。由于語音信號(hào)具有短時(shí)穩(wěn)態(tài)性,，因此基于壓縮感知的語音處理要先對信號(hào)進(jìn)行編幀,，然后利用隨機(jī)觀測矩陣對每幀信號(hào)壓縮采樣，最后逐幀恢復(fù)原信號(hào),。

　　實(shí)驗(yàn)仿真選用的一段女生聲音內(nèi)容為“hello,，酷狗”，共有44 100個(gè)樣點(diǎn),，采樣率為22.05 kS/s[5-6],。

　　1.1 自適應(yīng)信號(hào)稀疏

　　DCT是語音信號(hào)處理中應(yīng)用較多的稀疏方法，具有很強(qiáng)的能量集中功能,。但它屬于正交基變換,，信號(hào)的稀疏變換唯一，正交基的選擇影響稀疏性,，進(jìn)而影響信號(hào)重構(gòu),。冗余字典可以使信號(hào)呈現(xiàn)最佳稀疏，需要遵循各個(gè)基向量使輸入信號(hào)達(dá)到最佳稀疏的原則,?；谶@種原則，冗余字典是一定非正交并且冗余的矩陣,，可以通過增加稀疏基的梳理來提高變換系統(tǒng)的冗余性,，進(jìn)而增強(qiáng)信號(hào)逼近的靈活性，同時(shí)也提高了稀疏表示高階信號(hào)的能力,。研究采用基于K-均值的K-SVD算法作為自適應(yīng)冗余字典對語音信號(hào)稀疏,。K-SVD算法的方程表示為：

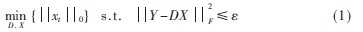
　　KSVD算法的相對誤差和平均幀重構(gòu)信噪比(AFSNR)示意如圖1。KSVD算法的平均幀重構(gòu)信噪比如表1所示,。

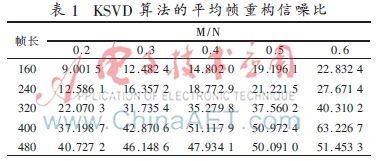
　　由表1的數(shù)據(jù)得到結(jié)論：經(jīng)過KSVD算法稀疏得到重構(gòu)語音的AFSNR隨幀長和信號(hào)壓縮比的增加而增大。

　　1.2 自適應(yīng)觀測矩陣

　　觀測矩陣的設(shè)計(jì)原則是與稀疏矩陣盡可能不相干,，且自身的列矩陣之間相互獨(dú)立,。隨機(jī)觀測矩陣具有上述特點(diǎn)，如高斯矩陣等,。在語音信號(hào)觀測投影時(shí)首先對信號(hào)進(jìn)行編幀,，然后選擇與稀疏矩陣盡量不相干的觀測矩陣相乘,，得到觀測值。

　　語音信號(hào)信號(hào)壓縮比值越大,，恢復(fù)信號(hào)的質(zhì)量就越高,；但觀測值越多，其恢復(fù)時(shí)間也越長,。根據(jù)語音信號(hào)每幀信息量的大小,，選擇相應(yīng)的觀測數(shù)，即自適應(yīng)觀測,；能量大的幀分配較多的觀測數(shù),，能量小的幀分配較小的觀測數(shù)，噪聲大部分存在于能量較小的幀,，較少的觀測數(shù)能起到去噪的作用,。

　　對已知的語音信號(hào)進(jìn)行自適應(yīng)觀測，得到的相對誤差和平均幀重構(gòu)信噪比（AFSNR）如圖2所示,。

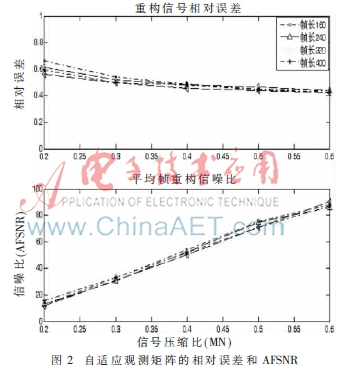
　　圖2的相對誤差表明,，語音信號(hào)的幀長對自適應(yīng)觀測的相對誤差值幾乎沒有影響，而壓縮比的值對信號(hào)相對誤差影響也較小,，自適應(yīng)觀測的相對誤差集中在0.45左右,。

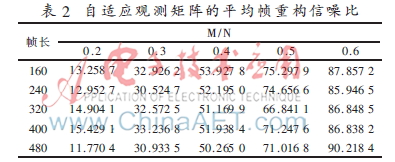
　　自適應(yīng)觀測矩陣的重構(gòu)語音質(zhì)量的好壞與壓縮比有直接關(guān)系，但每幀信號(hào)的幀長大小對重構(gòu)語音的影響微乎其微,，如表2所示,。

　　1.3 自適應(yīng)重構(gòu)算法

　　重構(gòu)信號(hào)是利用優(yōu)化求解的方法從觀測值和稀疏矩陣中重構(gòu)原信號(hào)。重建算法的設(shè)計(jì)應(yīng)遵循如下原則：算法應(yīng)使用較少的觀測值,，并且能精確和快速地恢復(fù)原信號(hào),。重構(gòu)語音需要對每幀語音信號(hào)逐一進(jìn)行恢復(fù)。常用的信號(hào)重構(gòu)算法有BP(Basic pursuit)算法和OMP算法,。

　　稀疏自適應(yīng)匹配追蹤算法（Sparse Adaptive Matching Pursuit,，SAMP）是基于OMP算法基礎(chǔ)上提出的，SAMP算法的主要思路是：在未知稀疏度的情況下進(jìn)行信號(hào)重構(gòu),，然后利用逐步加大步長的方法不斷增加所用的原子規(guī)模,，并引入回溯思想，在每次加大步長和選擇原子后,，都會(huì)與上步的原子合并,，最后從中選擇最佳的匹配原子。SAMP算法最大的優(yōu)點(diǎn)是在稀疏度未知的前提下能夠自適應(yīng)重構(gòu)原信號(hào),。

　　對已知語音信號(hào)采用SAMP算法進(jìn)行重構(gòu),，得到的相對誤差和平均幀重構(gòu)信噪比結(jié)果如圖3所示。

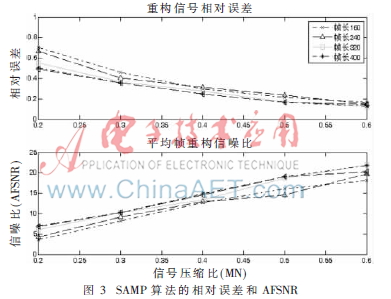
　　采用BP算法和OMP算法與SAMP算法進(jìn)行比較，AFSNR結(jié)果如圖4所示,。

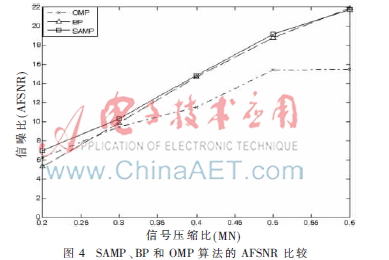
　　以重構(gòu)語音時(shí)間的角度評判,，運(yùn)行觀測矩陣約為1 s，剩余全部為重構(gòu)時(shí)間,，SAMP算法用時(shí)在10 s內(nèi),，OMP算法最少時(shí)間是10 s，而隨著壓縮比的增大,，重構(gòu)時(shí)間最高可達(dá)400 s,，BP算法時(shí)間更長，最小為40 s,，最高為2 500 s,。因此使用SAMP算法會(huì)大大減小壓縮感知重構(gòu)語音的時(shí)間。

2 自適應(yīng)壓縮感知

　　語音自適應(yīng)壓縮感知的設(shè)計(jì)流程如圖5所示,。

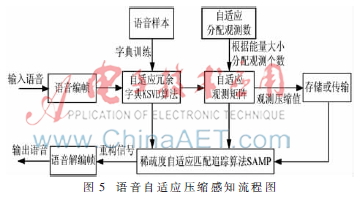
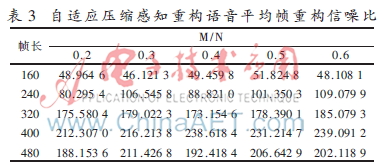
　　自適應(yīng)壓縮感知重構(gòu)語音平均幀重構(gòu)信噪比如表3所示,，表3的數(shù)據(jù)表明，幀長與信號(hào)壓縮比對重構(gòu)語音的質(zhì)量有積極影響,，而且信號(hào)壓縮比值較小的條件下,，恢復(fù)的語音質(zhì)量較高；在幀長400時(shí),，壓縮比的大小對重構(gòu)語音影響不大,，重構(gòu)的語音信號(hào)達(dá)到優(yōu)的級別，同時(shí)要遠(yuǎn)遠(yuǎn)高于KSVD算法,、自適應(yīng)觀測矩陣和SAMP算法單獨(dú)重構(gòu)語音的質(zhì)量,。3種自適應(yīng)算法組合一起能充分發(fā)揮各自的優(yōu)點(diǎn)，彌補(bǔ)了每個(gè)算法的缺陷：減少了KSVD所產(chǎn)生的噪聲,，重構(gòu)語音的相對誤差成倍的降低,，并且提高了重構(gòu)的AFSNR，使得語音的質(zhì)量更好,，同時(shí)提高了信號(hào)稀疏度,，降低了在重構(gòu)時(shí)計(jì)算的復(fù)雜度，從而進(jìn)一步減少重構(gòu)語音的時(shí)間,。

　　如圖6所示,，相對于普通壓縮感知，自適應(yīng)壓縮感知具有更好的重構(gòu)語音信號(hào)質(zhì)量,，采樣恢復(fù)語音時(shí)間更短,，而且在信號(hào)低壓縮的條件下，能恢復(fù)出良好的語音,。

3 結(jié)論

　　本文通過將自適應(yīng)算法引入壓縮感知,，結(jié)合自適應(yīng)冗余字典KSVD算法,、自適應(yīng)觀測矩陣和SAMP重構(gòu)算法，提出自適應(yīng)壓縮感知,，并分別進(jìn)行仿真分析，通過平均幀重構(gòu)信噪比,、相對誤差,，與普通壓縮感知進(jìn)行對比，驗(yàn)證了KSVD的稀疏的性能以及SAMP算法的優(yōu)勢,。最后對自適應(yīng)壓縮感知進(jìn)行仿真分析,，驗(yàn)證了將自適應(yīng)算法引入壓縮感知理論的可行性。

參考文獻(xiàn)

　　[1] CANDS E,，WAKIN M.An introduction to compressive sampling[J].IEEE Signal Processing Magazine,，2008，25(2)：21-30.

　　[2] CANDS E,，ROMBERG J,，TAO T.Robust uncertainty prin-ciples：exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory，2006,，52(2)：489-509.

　　[3] 余愷,，李元實(shí)，王智,，等.基于壓縮感知的新型聲信號(hào)采集方法[J].儀器儀表學(xué)報(bào),，2011，33(1)：106-112.

　　[4] 周小星,，王安娜,，孫紅英，等.基于壓縮感知過程的語音增強(qiáng)[J].清華大學(xué)學(xué)報(bào)(自然科學(xué)版),，2011,，51(9)：1234-1238.

　　[5] 羅武駿，陶文鳳,，左加闊,，等.自適應(yīng)語音壓縮感知方法[J].東南大學(xué)學(xué)報(bào)(自然科學(xué)版)，2012,，42(6)：1027-1030.

　　[6] 張雪英.數(shù)字語音處理及MATLAB仿真[M].北京：電子工業(yè)出版社,，2010.