鄧向林，唐飛岳

　?。ê辖煌殬I(yè)技術(shù)學(xué)院,，湖南 長(zhǎng)沙410132）

       摘要：電子商務(wù)的興起促進(jìn)了現(xiàn)代物流業(yè)的發(fā)展，但物流公司在貨物送達(dá)末梢客戶(hù)的“最后一公里”路徑規(guī)劃上,，多取決于具體配送人員的工作經(jīng)驗(yàn),，整體效率偏低,。為提高配送效率，對(duì)車(chē)輛路徑問(wèn)題(Vehicle Routing Problem, VRP),，以及由此延伸出的有載重限制的車(chē)輛路徑問(wèn)題(VRP with Capacitated, CVRP)的研究因而產(chǎn)生,。為提升現(xiàn)有的蜂群算法在CVRP問(wèn)題的求解效能，文章對(duì)蜂群算法進(jìn)行了改進(jìn),，在CVRP問(wèn)題中加入分群機(jī)制來(lái)限縮蜂群探索區(qū)域,，并搭配使用限制次數(shù)以增強(qiáng)對(duì)局部區(qū)域搜尋能力。模擬結(jié)果顯示,，在復(fù)雜度高的問(wèn)題求解上,，所提出的加強(qiáng)型蜂群算法比典型的蜂群算法能更有效地找到近似最佳解。

　　關(guān)鍵詞：車(chē)輛路徑問(wèn)題,；蜂群算法

　　中圖分類(lèi)號(hào)：TP29;F253.9文獻(xiàn)標(biāo)識(shí)碼：ADOI： 10.19358/j.issn.1674-7720.2017.01.017

　　引用格式：鄧向林,，唐飛岳. 基于蜂群算法的物流配送規(guī)劃研究［J］.微型機(jī)與應(yīng)用，2017,36（1）：56-58.

0引言

　　全國(guó)交通運(yùn)輸職業(yè)教育科研項(xiàng)目（2013B41）隨著現(xiàn)代物流行業(yè)的高速發(fā)展,，其已成為支持城市經(jīng)濟(jì)的重要?jiǎng)恿εc基礎(chǔ),，但物流行業(yè)的運(yùn)輸行為也對(duì)城市帶來(lái)了交通擁塞、環(huán)境污染等負(fù)面影響,，因此物流行業(yè)的運(yùn)營(yíng)能力水平高低成為評(píng)估城市區(qū)域競(jìng)爭(zhēng)力的關(guān)鍵因素之一,。 車(chē)輛路徑問(wèn)題是對(duì)物流配送行為的一種運(yùn)籌與模擬，目前絕大部分的車(chē)輛路徑問(wèn)題都是NP難題,，為有效解決此類(lèi)問(wèn)題,，相應(yīng)的新興算法由此產(chǎn)生，蜂群算法以其較強(qiáng)的全局尋優(yōu)能力以及較快的收斂速度得到了廣泛的應(yīng)用,。

1研究背景

　　社會(huì)的進(jìn)步與現(xiàn)代科技的發(fā)展帶來(lái)了以網(wǎng)絡(luò)購(gòu)物為典型應(yīng)用的電子商務(wù)活動(dòng)的驟增,，這也推動(dòng)了物流行業(yè)的變革。按傳統(tǒng)B2B的物流配送方式,，貨物需經(jīng)廠(chǎng)商,、中間商、分銷(xiāo)商,、零售商才能送達(dá)消費(fèi)者手中,，這已經(jīng)無(wú)法滿(mǎn)足在線(xiàn)購(gòu)物的需求。直接送貨上門(mén)的C2C模式成為更受歡迎的新方式,。目前物流公司多在收送貨物后，才讓該區(qū)域配送人員考慮路線(xiàn)問(wèn)題,，但這往往取決于配送人員本身的經(jīng)驗(yàn),，因行駛距離、配送時(shí)間的不確定性使得配送成本難以控制,。

　　最早的車(chē)輛路程問(wèn)題(Vehicle Routing Problem, VRP)由DANTZIG G B和RAMSER J H在1959 年首次提出［1］,，迄今為止仍然是國(guó)內(nèi)外研究的難點(diǎn)問(wèn)題,，由于VRP問(wèn)題是屬于NPcomplete 問(wèn)題，因此在傳統(tǒng)的VRP問(wèn)題上只能找到近似最佳解,。隨著VRP復(fù)雜度的提高與問(wèn)題模式的改良,，其困難度也呈指數(shù)型成長(zhǎng)［2］。傳統(tǒng)蟻群算法求解小型VRP問(wèn)題相當(dāng)便捷,，該算法主要是建構(gòu)一條路徑再藉由費(fèi)洛蒙的揮發(fā)程度去更改路徑,，每條路徑上都必須計(jì)算移轉(zhuǎn)率并判別行駛該路線(xiàn)的可能性，且?guī)缀醵紴閱吸c(diǎn)的路徑改善,，并無(wú)蜂群算法多樣化的鄰近搜尋方式,，因此當(dāng)數(shù)據(jù)結(jié)構(gòu)增大，蟻群算法在效率及準(zhǔn)確性上就會(huì)相對(duì)降低,。隨著C2C模式物流配送需求度的不斷增長(zhǎng),，為了提高貨物送達(dá)客戶(hù)的效率，對(duì)于貨物配送路線(xiàn)的優(yōu)化成為需要研究的決策支持問(wèn)題,。

2CVRP問(wèn)題描述

　　本文對(duì)車(chē)輛載重限制的CVRP（VRP with Capacitated, CVRP）問(wèn)題,，即從起始點(diǎn)(倉(cāng)庫(kù))配貨至各個(gè)客戶(hù)的最優(yōu)路線(xiàn)問(wèn)題進(jìn)行探討。對(duì)本文所研究CVRP問(wèn)題條件設(shè)置為：

　?。?）倉(cāng)庫(kù)：只有一個(gè)配送貨物的定點(diǎn)倉(cāng)庫(kù),，且只考慮單純配送情形；

　?。?）車(chē)輛：每輛貨車(chē)只有單位100 的貨物裝載量,，并且只考慮單一車(chē)種問(wèn)題，貨車(chē)均由倉(cāng)庫(kù)出發(fā),，行駛過(guò)每個(gè)指派的需求點(diǎn),，且車(chē)輛沒(méi)有油耗、維修等問(wèn)題,；

　?。?）客戶(hù)點(diǎn)與客戶(hù)需求：每位客戶(hù)的地點(diǎn)與需求都為已知；

　?。?）行駛路線(xiàn)：每輛貨車(chē)都必須到達(dá)指派地點(diǎn),；

　　（5）求解目標(biāo)為：對(duì)一系列需要到訪(fǎng)的載貨點(diǎn)與卸貨點(diǎn),，組成合理的最短路程,，使貨車(chē)按照規(guī)定的行車(chē)路線(xiàn)去行駛，在滿(mǎn)足貨車(chē)容量限制條件的同時(shí),，使路程最短,、整體使用車(chē)輛最少。

　　對(duì)本文研究的CVRP問(wèn)題數(shù)學(xué)模型描述如下：首先必須對(duì)n個(gè)客戶(hù)送貨，第i個(gè)客戶(hù)的需求量為di(i=1,2,3…,n),，由倉(cāng)庫(kù)派出m輛車(chē)來(lái)載運(yùn),，第t輛車(chē)容量為ct(t=1,2,3…,m)，將貨物送往各個(gè)客戶(hù),，最后再回到倉(cāng)庫(kù),。限制條件為：

　　(1)每輛貨車(chē)的載貨量不得超過(guò)該輛貨車(chē)的最大載貨量；

　　(2)每個(gè)客戶(hù)最多只能由一輛貨車(chē)拜訪(fǎng),；

　　(3)每一條配送路線(xiàn)的長(zhǎng)度不得超過(guò)貨車(chē)的最大行駛距離,；

　　(4)客戶(hù)的配送順序不變，例如必須在拜訪(fǎng)a點(diǎn)之前先到b點(diǎn),。

　　最終目標(biāo)為運(yùn)輸總成本最小(車(chē)輛最少,、路徑最短)，如式（1）所示：

　　其中,，Cij表示從客戶(hù)i到客戶(hù)j的運(yùn)輸成本,，Xijt表示車(chē)輛t是否由i到j(luò)。Xijt是決策變量,，1表示是,，0表示否。

　　若配送到ij點(diǎn)必須由t車(chē)輛單獨(dú)完成,，分別記為yit,、yjt，如式（2）所示：

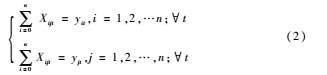
　　限制每輛車(chē)的載貨量不得超過(guò)該輛車(chē)的最大載貨量qt,，如式（3）所示：

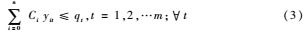
　　每個(gè)客戶(hù)只能由一輛車(chē)完成,而整個(gè)VRP 任務(wù)則由m輛車(chē)共同完成,。分別如式（4）、（5）所示：

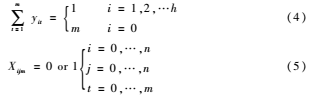
3蜂群算法改善設(shè)計(jì)

　　蜂群算法是2005年由KARABOGA D提出的一種啟發(fā)式算法［3］,，分別由工蜂,、觀(guān)察蜂、探索蜂來(lái)執(zhí)行趨近局部?jī)?yōu)化解,，再效仿蜜蜂群集智慧將最佳解突顯出來(lái),，在效率上比起以往的算法都有顯著的提升，較適用于解決多目標(biāo)的函數(shù)問(wèn)題,。在一般仿生式算法中,，初始解幾乎都為隨機(jī)式，在數(shù)據(jù)較小時(shí)雖能求出近似最佳解,，但隨著數(shù)據(jù)變大,，復(fù)雜度也成指數(shù)型增長(zhǎng)，而在使用鄰近求解的過(guò)程中,，效率因而降低［46］,。本文基于蜂群算法進(jìn)行改善,，結(jié)合掃描法使得整體的搜索空間縮小，對(duì)初始解的產(chǎn)生方法予以改變,。

　　首先工蜂負(fù)責(zé)的工作內(nèi)容為產(chǎn)生初始解,每只工蜂代表一個(gè)解（工蜂數(shù)量以FS表示）。接著計(jì)算該初始解是否超過(guò)本貨車(chē)的負(fù)載量(如超過(guò)則再加一臺(tái)貨車(chē)),，然后按式（6）從所有的初始解中計(jì)算適應(yīng)值并產(chǎn)生可能的候選解,。

　　工蜂產(chǎn)生初始解前，將先對(duì)原本無(wú)規(guī)律的節(jié)點(diǎn)進(jìn)行有順序性的分群,，再將節(jié)點(diǎn)依序劃分為4個(gè)群,，使工蜂的搜尋面積由整個(gè)搜尋區(qū)塊縮小成4個(gè)等份。降低單個(gè)工蜂的搜尋面積再進(jìn)一步將所求得的解交至觀(guān)察蜂收斂,。

　　觀(guān)察蜂主要是從工蜂所產(chǎn)生的候選解中每個(gè)逐步地鄰近搜尋,，對(duì)初始解進(jìn)行鄰近搜尋(采用隨機(jī)置換解、隨機(jī)插入解,、隨機(jī)反轉(zhuǎn)解,、隨機(jī)反轉(zhuǎn)與插入解的組合策略)，計(jì)算該鄰近解的適應(yīng)值并讓觀(guān)察蜂判斷此鄰近解是否小于原初始解,，是則進(jìn)入探索蜂階段,，否則重復(fù)臨近搜索。觀(guān)察蜂數(shù)量以O(shè)B表示,。

　　探索蜂的工作內(nèi)容為判斷觀(guān)察蜂的搜尋狀況,，找出個(gè)解的最大限制次數(shù)，判斷其是否大于探索蜂的限制次數(shù)(max_limit),，若是則由探索蜂隨機(jī)找出一解,，否則告知觀(guān)察蜂繼續(xù)對(duì)該食物源進(jìn)行搜尋。

4實(shí)驗(yàn)?zāi)M與結(jié)果分析

　　本研究以MATLAB 7.10.0(R2010a)編寫(xiě)程序,，執(zhí)行代碼的服務(wù)器主要配置為Intel(R)2.53 GHz 處理器/內(nèi)存4 GB,。實(shí)驗(yàn)樣本是CVRP 標(biāo)準(zhǔn)數(shù)據(jù)集來(lái)作為測(cè)試樣本，每組數(shù)據(jù)皆進(jìn)行20次統(tǒng)計(jì)測(cè)試,。將工蜂數(shù),、迭代數(shù)逐步增大，對(duì)比典型蜂群算法與本文改進(jìn)的蜂群算法所求得的平均路徑成本,，其結(jié)果如表1所示,。

　　取其中最低路徑成本的參數(shù)值,即FS=100、Iterations=1 000,，再分別代入不同的探索蜂的限制次數(shù)參數(shù)（max_limit）進(jìn)行兩種算法的效能對(duì)比,，如表2所示。

　　由于分群法其主要目的就是規(guī)律性地限縮其探索范圍,，至此將所求得的優(yōu)化參數(shù)（即FS=100,、Iterations=1 000,、max_limit=100）代入不同客戶(hù)數(shù)量數(shù)據(jù)集中，兩種算法的效能對(duì)比結(jié)果見(jiàn)表3,。

　　從實(shí)驗(yàn)數(shù)據(jù)可以看出,，在客戶(hù)節(jié)點(diǎn)數(shù)小于60時(shí)，以典型蜂群算法的成本較佳,，但在客戶(hù)節(jié)點(diǎn)數(shù)超過(guò)60后,，本文所提出的蜂群算法較佳。若客戶(hù)節(jié)點(diǎn)數(shù)持續(xù)增長(zhǎng),，由于本文所用的改進(jìn)蜂群算法在初始解產(chǎn)生方式上明顯優(yōu)于典型蜂群算法,，其成本優(yōu)勢(shì)將更為明顯。

5結(jié)論

　　本文主要是對(duì)典型蜂群算法進(jìn)行改善,，用于針對(duì)CVRP問(wèn)題求解,。有別于以往的仿生式算法，研究中使用分群式產(chǎn)生規(guī)律性的初始解,，并使用單點(diǎn)置換法作為鄰近搜索主要求解法,，然后以滿(mǎn)足搜索限制條件為約束，使用單一置換,、反轉(zhuǎn)法,、插入法的組合搜尋策略，實(shí)驗(yàn)數(shù)據(jù)證實(shí)了本文所提出的加強(qiáng)型蜂群算法可減少算法的計(jì)算開(kāi)銷(xiāo),。

　　參考文獻(xiàn)

　?。?］ DANTZIG G B， RAMSER J H.The truck dispatching problem［J］. Management Science, 1959(6):80-91.

　?。?］ CHRISTOFIDES N, MINGOZI A, TOTH P. The vehicle routing problem［M］.  New York: John Wiley & Sons,1978:318-338.

　?。?］ KARABOGA D. An idea based on honey bee swarm for numerical optimization［R］. Technical ReportTR06, Erciyes University,2005

　　［4］ KARABOGA D, BASTURK B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm［J］. Journal of Global Optimization,2007,39(3):459-471.

　?。?］ KARABOGA D, BASTURK B. On the performance of artificial bee colony (ABC) algorithm［J］. Soft Computing,2008,8(1): 687-697.

　?。?］ KARABOGA N. A new design method based on artificial bee colony algorithm for digital IIR filters［J］. Journal of the Franklin Institute,2009,346(4):328-348.