董智鵬

　　(桂林電子科技大學(xué) 機電工程學(xué)院,，廣西 桂林 541004)

       摘要：微位移精密定位系統(tǒng)中的壓電陶瓷元器件具有非光滑特性，無法直接測得壓電元器件的輸入輸出信號,，常規(guī)方法難以對其進行有效的辨識和控制,。文章采用三明治模型來描繪納米微位移平臺，并提出一種基于最小二乘支持向量機優(yōu)化的辨識方法解決三明治遲滯模型的辨識問題,。最后基于已經(jīng)辨識的三明治模型,，設(shè)計一個PID逆補償控制器，解決定位系統(tǒng)的精密軌跡控制問題,。

　　關(guān)鍵詞：三明治系統(tǒng),；遲滯,；最小二乘支持向量機,；逆補償前饋控制

　　中圖分類號：TP273.1文獻(xiàn)標(biāo)識碼：ADOI： 10.19358/j.issn.1674-7720.2017.03.017

　　引用格式：董智鵬.MPT系列微位移定位系統(tǒng)的辨識與控制［J］.微型機與應(yīng)用，2017,36（3）：55-58.

　0引言

　　微位移定位平臺主要應(yīng)用于天文射電望遠(yuǎn)鏡,。因其具有反應(yīng)速度快和輸出大等特點［13］也適用于工廠自動化中的精確定位,。經(jīng)過柔性鉸鏈裝置將微小的位移量進一步放大，從而得到所需要的實際信號輸出,。為了獲得精準(zhǔn),、可控的微位移運動軌跡，直接加載在壓電器件上的壓電信號較大,。因此,，由控制器產(chǎn)生的弱電控制信號必須經(jīng)過調(diào)制解調(diào)、放大等處理,。圖1描述了PEA的工作過程,。遲滯環(huán)節(jié)的兩端可以直接線性化處理；但具有逆壓電效應(yīng)的壓電陶瓷是一個非光滑非線性遲滯系統(tǒng),。精密定位系統(tǒng)中的遲滯環(huán)節(jié)不僅會降低控制精度,，更嚴(yán)重的還會使得控制系統(tǒng)發(fā)散［2 3］。所以對遲滯三明治系統(tǒng)的辨識一直是個熱點。

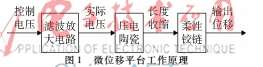
1含有遲滯三明治系統(tǒng)的描述和分析

　　根據(jù)文獻(xiàn)［4］對微位移系統(tǒng)的定義,，三明治系統(tǒng)是兩端線性環(huán)節(jié)中間夾著一個非線性環(huán)節(jié)的模型結(jié)構(gòu),，如圖2所示。

　　圖2中,，L1(·)和L2(·)表示線性動態(tài)環(huán)節(jié),，H(·)表示非線性環(huán)節(jié)；u(k)為輸入信號,y(k)為輸出信號,ω1(k)為中間環(huán)節(jié)的輸入信號,ω2(k)是中間環(huán)節(jié)的輸出信號,。本文采用ARMRAX模型來描述L1(·)和L2(·),，則微位移定位系統(tǒng)可表示為：

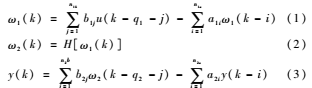
　　式中，n1a和n1b,、a1i和a2i分別為L1(·)和L2(·)的階次和權(quán)重,，q1和q2為純延時；非線性環(huán)節(jié)由函數(shù)H(·)描述,。

2基于LSSVM的三明治系統(tǒng)辨識

　　2.1最小二乘支持向量機

　　與標(biāo)準(zhǔn)的ε支持向量機相比,，LSSVM在樣本不是很大的情況下具有較好的擬合性。其基本思想也是通過在高維空間構(gòu)造決策函數(shù)y(x)再引進內(nèi)積變換和相應(yīng)的核函數(shù),。

　　y(x)=sgn［ω(x)+b］（4）

　　對于最小二乘支持向量機,，尋優(yōu)問題為：

　　為求解上述尋優(yōu)問題，需要構(gòu)造拉格朗日等式,，把約束決策問題變?yōu)闊o約束超平面問題：

　　式中,αi(i=1,2,…,，n)是Lagrange權(quán)值。

　　根據(jù)KuhnTucker條件,得:

　　

　　可以發(fā)現(xiàn)最小二乘支持向量機的訓(xùn)練實際上是通過奇異值分解法求解一個線性方程組,。

　　2.2線性環(huán)節(jié)辨識

　　在三明治系統(tǒng)中,，遲滯環(huán)節(jié)H(·)不僅具有非光滑、次環(huán),、多值映射等復(fù)雜特性,，而且無法測得其信號，現(xiàn)有的辨識方法很難奏效,。從圖3（a）中可知,，遲滯具有復(fù)雜的特性。首先設(shè)計一個退化激勵信號［5］,將遲滯環(huán)節(jié)限制在單調(diào)上升的模態(tài)之中,，即：

　　ω2(k)=f［ω1(k)］（10）

　　退化后的單模態(tài)遲滯環(huán)節(jié)如圖3（b）所示,。

　　這樣就可以將線性環(huán)節(jié)辨識出來，在具體編寫程序時采用增量斜坡信號代替原始信號,。根據(jù)文獻(xiàn)［6］的關(guān)鍵項分離原則,，于是式（1）~式（3）所描述的系統(tǒng)構(gòu)建了一個具有參數(shù)線性化結(jié)構(gòu)的整體模型。

　　這樣就可以采用廣義梯度算法［7］來辨識兩端線性環(huán)節(jié),。

　　2.3動態(tài)遲滯環(huán)節(jié)的辨識

　　重新設(shè)計一個正弦衰減信號形式如下：

　　式中：φ是相位,，γ是幅值偏置；Am和fm是信號的峰值和截止頻率，α和β是幅值和信號的退化系數(shù),。根據(jù)2.2節(jié)已經(jīng)辨識的線性環(huán)節(jié)將遲滯環(huán)節(jié)的輸入輸出信號重構(gòu)出來,，即

　　由文獻(xiàn)［8 9］可得“基于最小二乘支持向量機”所構(gòu)造的微位移模型可以很好地描述遲滯的復(fù)雜特性，尤其是參數(shù)具有較好的冗余性,，可以降低計算機的故障率,。從而使得PEA具有更高的運動精度，因此本文采用LSSVM代表遲滯環(huán)節(jié),。

3基于三明治模型的軌跡控制器設(shè)計

　　根據(jù)已經(jīng)辨識的遲滯三明治模型及其逆模型,，設(shè)計一個帶有逆補償控制器的系統(tǒng)，如圖4所示,。

　　圖4中,，r(k)、e(k),、u(k),、y(k)分別為閉環(huán)控制信號；ω(k)和v(k)為對象及其逆模型的中間信號,?？刂破饔蓛刹糠纸M成：逆補償控制器和前向控制器，uf(k)和up(k)分別表示系統(tǒng)中兩個子控制器的輸出信號,，且有：

　　u(k)=uf(k)+up(k)（15）

　　在所設(shè)計的控制器中,，逆補償控制器由三明治系統(tǒng)逆模型構(gòu)成，用于抵消PEA中的遲滯特性,。另一方面,，當(dāng)逆模型存在建模誤差或者系統(tǒng)受到外界干擾產(chǎn)生誤差綜上，從性能指標(biāo)可以看出,，本文算法對含有不同程度高斯噪聲或者椒鹽噪聲的巖石顆粒圖像的去噪表現(xiàn)良好,，優(yōu)于基于Contourlet的BayesShrink去噪效果。

4實驗結(jié)果

　　采用江蘇匯博公司生產(chǎn)的MPT系列壓電陶瓷執(zhí)行器來驗證所提出的辨識和控制方案,。額定輸入電壓和輸出位移為10 V和10 μm；控制器由研華公司生產(chǎn)的PCL818LS型組成,，使用Turbo C編寫控制程序,，采用控制頻率為33 kHz。

　　4.1辨識結(jié)果

　　(1)線性環(huán)節(jié)辨識信號采用M序列,，幅值mf=3 mV,，斜率mA=10>2 mf。這樣就可以使遲滯特性限制在單調(diào)上升模態(tài)內(nèi),，具體在相關(guān)程序中可以采用3階多項式逼近,。接下來采用關(guān)鍵項分離原理［6］來辨識兩端線性環(huán)節(jié)，RGIA的初始值為：P(0)=1.0×106×I(6)，γ(0)=0.001,，θ(0)=0.001×J(1,6),。e(k－1)2+e(k)2<ε是判斷線性環(huán)節(jié)收斂的依據(jù)，式中ε=10－8,，I是單位陣,，J是單位行向量。經(jīng)過608步迭代后收斂,，圖5是線性模型參數(shù)的收斂過程,。

　　(2)重新設(shè)計一個正弦衰減信號：

　　(3)采用最小二乘支持向量機來辨識遲滯環(huán)節(jié)的神經(jīng)網(wǎng)絡(luò)模型。核函數(shù)選取高斯徑向基函數(shù),，經(jīng)過32次迭代后神經(jīng)網(wǎng)絡(luò)收斂,，如圖6所示。

整個系統(tǒng)辨識完成后,，還需要設(shè)計一個正弦調(diào)制信號來驗證建模的精度,。

　　uv(k)=(3.0×e－10×k)×［sin(2π×(300×e－20×k))+1.0］(17)

　　并且在檢驗信號中隨機加入一個幅值為10 V、寬度為0.1 ms的強干擾噪聲,。對應(yīng)的模型檢驗結(jié)果如圖7所示,。實驗證明，該建模方法具有良好的動態(tài)性能,。

　　4.2軌跡控制結(jié)果

　　實驗中,，控制頻率fs=33 kHz，由于過高的電壓可能會破壞電路,，所以需要對輸入信號u(k)進行一定限制,，具體限制在［-10,10］之間。依據(jù)式(13）,、（14),，可以首先將補償環(huán)節(jié)上的逆模型－11(·)和－12(·)計算出來，再由相應(yīng)的遲滯環(huán)節(jié)辨識結(jié)果,，利用每次給出的反饋來不斷訓(xùn)練對應(yīng)的遲滯逆模型,。最終的前向控制器C(·)被設(shè)計為：C(·):Kp=1.120 4;Ki=0.382 0;Kd=0.152 0;被控對象的輸入輸出如圖8所示,。

　　為了更好地說明本建模方法的優(yōu)越性,，本文還采用了普通PID控制器進行軌跡的預(yù)測控制,，在編程過程中進行了一系列的微調(diào),，最終的PID控制器參變量為：Kp=1.756,，Ki=0.627和Kd=4.234,，軌跡跟蹤對比如圖9所示,。

5結(jié)論

　　經(jīng)過一系列的實驗論證,，所提出的辨識方案與實際軌跡對比具有很小的誤差,；在此基礎(chǔ)上設(shè)計的逆補償控制器不僅精度很高,，而且動態(tài)效果很好,，完全滿足了微位移控制的要求。

　　參考文獻(xiàn)

　?。?］ GE P. Modeling and control of hysteresis in piezoceramic actuator ［D］. Kingston: University of Rhode Island, 1996.

　?。?］ HU H.Compensation of hysteresis in piezoceramic actuators and control of nanopositioning system ［D］. Toronto: University of Toronto, 2003.［3］ MAYERGOYZ I D. Mathematical models of hysteresis［M］. New York: SpringerVerlag, 1991.

　　［4］ TAWARE A, TAO G. Control of sandwich nonlinear systems ［M］.New York: Springer, 2003.

　?。?］ 謝揚球,譚永紅.壓電陶瓷執(zhí)行器的非光滑三明治模型辨識與內(nèi)?？刂疲跩］.控制理論與應(yīng)用，2013,30（5）：567-576.

　?。?］ TAN Y H,DONG R L,LI R Y.Recursive identification of sandwich system with deadzone and application［J］.IEEE Transactions on Control System Technology,2009,17(4):945-951.

　?。?］ 方崇智,蕭德云.過程辨識［M］.北京：清華大學(xué)出版社,2004.

　　［8］ 閻威武,邵惠鶴.支持向量機和最小二乘支持向量機的比較及應(yīng)用研究［J］.控制與決策,，2003,18（3）：358-360.

　?。?］ 桂衛(wèi)華，宋海鷹,，楊春華.HammersteinWiener模型最小二乘向量機辨識及其應(yīng)用［J］.控制理論與應(yīng)用,，2008,25（3）：393-397.