熊群芳,陶青川,葉重陽(yáng)
(四川大學(xué) 電子信息學(xué)院,四川 成都 610065)
摘要:提出一種基于雙線陣相機(jī)的全視角高精度三維測(cè)量系統(tǒng),實(shí)現(xiàn)對(duì)空間大尺寸物體三維測(cè)量。首先,通過兩臺(tái)高速線陣相機(jī)結(jié)合高精度單軸回轉(zhuǎn)平臺(tái)、高速圖像采集卡對(duì)空間物體掃描成像,然后利用空間前方交會(huì)原理以及空間三維測(cè)量系統(tǒng)定向解算出空間物體的實(shí)際空間三維坐標(biāo)。該三維測(cè)量系統(tǒng)的優(yōu)點(diǎn)是不必提前對(duì)線陣相機(jī)進(jìn)行內(nèi)參標(biāo)定,且自動(dòng)化程度高,測(cè)量速度快。實(shí)驗(yàn)結(jié)果表明,該三維測(cè)量系統(tǒng)精度高,可以廣泛地運(yùn)用到大尺寸空間測(cè)量領(lǐng)域,具有良好的實(shí)用價(jià)值。
關(guān)鍵詞:雙線陣相機(jī);三維測(cè)量系統(tǒng);高精度
中圖分類號(hào):TN911.73;TN247文獻(xiàn)標(biāo)識(shí)碼:ADOI: 10.19358/j.issn.1674-7720.2017.05.014
引用格式:熊群芳,陶青川,葉重陽(yáng).基于雙線陣相機(jī)的全視角高精度三維測(cè)量系統(tǒng)[J].微型機(jī)與應(yīng)用,2017,36(5):42-45,49.
0引言
隨著計(jì)算機(jī)機(jī)器視覺這一新興學(xué)科的興起以及科學(xué)技術(shù)和航天工業(yè)[12]的發(fā)展,非接觸式空間三維測(cè)量系統(tǒng)在視覺測(cè)量領(lǐng)域中占有越來越重要的地位。近幾年,以經(jīng)緯儀作為傳感器,用兩臺(tái)或兩臺(tái)以上經(jīng)緯儀配合計(jì)算機(jī)及相應(yīng)的硬件、軟件所組成的空間坐標(biāo)測(cè)量系統(tǒng)在工程測(cè)量以及計(jì)量學(xué)中得到廣泛的應(yīng)用[34]。經(jīng)緯儀系統(tǒng)雖是非接觸式的,但在測(cè)量的過程中必須通過專用測(cè)量孔或粘貼瞄準(zhǔn)靶標(biāo)來指示目標(biāo),基準(zhǔn)孔的制造誤差對(duì)建立坐標(biāo)系所帶來的誤差影響很大。基于非接觸式面陣相機(jī)的大尺寸測(cè)量系統(tǒng)[5],由于不需要逐點(diǎn)測(cè)量,實(shí)時(shí)性好,大大提高了測(cè)量效率,但由于面陣相機(jī)圖像分辨率受限,需要移動(dòng)設(shè)備進(jìn)行多位置測(cè)量,不能快速完成全尺寸測(cè)量。
針對(duì)傳統(tǒng)經(jīng)緯儀自動(dòng)化程度低、測(cè)量精度低、面陣相機(jī)圖像分辨率受限等不足,本文提出一種基于雙目線陣相機(jī)的全視角高精度三維測(cè)量系統(tǒng),采用交會(huì)測(cè)量原理,結(jié)合高分辨率線陣相機(jī)、高精度回轉(zhuǎn)平臺(tái)、圖像靶標(biāo)提取等設(shè)備和方法,構(gòu)建了一個(gè)自動(dòng)化程度高、測(cè)量速度快的全視角三維測(cè)量系統(tǒng),可一次性實(shí)現(xiàn)空間物體大量特征點(diǎn)的三維坐標(biāo)測(cè)量。
1測(cè)量系統(tǒng)基本原理
1.1空間前方交會(huì)原理
測(cè)量系統(tǒng)用兩臺(tái)相同的CMOS線陣相機(jī)以及高精度回轉(zhuǎn)平臺(tái)構(gòu)成全視角高精度采集儀,采用空間前方交會(huì)原理[6]。如圖1所示,A、B兩臺(tái)采集儀,以A中線陣相機(jī)的光心為坐標(biāo)原點(diǎn),A、B連線在水平方向的投影為X軸,過A的鉛錘方向?yàn)閆軸,以右手法則確定Y軸,以此構(gòu)成測(cè)量坐標(biāo)系。
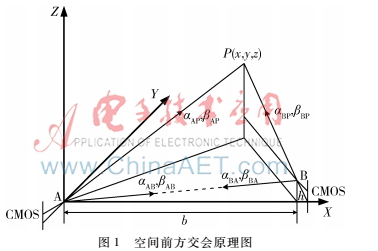
其中,A、B互瞄以及分別從A、B觀測(cè)目標(biāo)P的觀測(cè)值(水平方向和豎直方向的旋轉(zhuǎn)角度)分別為:αAB、βAB、αBA、βBA、αAP、βAP、αBP、βBP,A、B兩臺(tái)采集儀掃描目標(biāo)P的水平旋轉(zhuǎn)角度和豎直旋轉(zhuǎn)角度滿足下式:
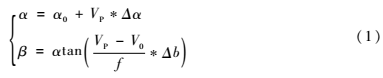
式(1)中,α為采集儀掃描目標(biāo)P在水平面的水平旋轉(zhuǎn)角度。α0為掃描靶標(biāo)時(shí)的起始角度,由兩個(gè)高精度回轉(zhuǎn)平臺(tái)給定,為已知值。Δα為圖像中一個(gè)像素對(duì)應(yīng)的旋轉(zhuǎn)角度,由回轉(zhuǎn)平臺(tái)給定,為已知值。Δb為像元尺寸。VP包括VAP、VBP,為目標(biāo)P在A、B相機(jī)成像的豎直方向的像素坐標(biāo),通過靶標(biāo)提取算法可以得到。β為采集儀測(cè)量裝置掃描目標(biāo)P在垂直面的豎直旋轉(zhuǎn)角度。V0包括V0A、V0B,分別為采集儀測(cè)量裝置中線陣相機(jī)A和B的主點(diǎn)。f包括fA、fB,為采集儀測(cè)量裝置A和B中線陣相機(jī)的焦距。
令水平旋轉(zhuǎn)角αA、αB為:

式中,b為基線長(zhǎng)(即兩儀器A、B的水平間距),h為兩全視角高精度采集儀器的高差,且有:

由式(3)、(4)可知,建立了被測(cè)點(diǎn)的空間坐標(biāo)系,此時(shí)只需求出式中未知參數(shù)基線b、h、αAB、αBA、V0A、fA、V0B、fB,即可得到P的空間坐標(biāo)。
1.2圖像采集
線陣相機(jī)每次成像僅為一列像素,要完成圖像采集,需移動(dòng)相機(jī)或者移動(dòng)待成像物體。將相機(jī)安裝在水平放置的回轉(zhuǎn)平臺(tái)上,通過轉(zhuǎn)臺(tái)的旋轉(zhuǎn),完成對(duì)物體的成像。線陣相機(jī)設(shè)置為外觸發(fā)模式,由轉(zhuǎn)臺(tái)提供觸發(fā)脈沖,轉(zhuǎn)臺(tái)每轉(zhuǎn)動(dòng)一定的角度就發(fā)送一個(gè)觸發(fā)脈沖,相機(jī)就在對(duì)應(yīng)位置采集一列像素,那么圖像的每一列都對(duì)應(yīng)一個(gè)轉(zhuǎn)臺(tái)角度,這樣就把圖像像素坐標(biāo)與空間實(shí)際角度對(duì)應(yīng)起來了。在左右相機(jī)掃描獲得的圖像中,通過靶標(biāo)提取算法,獲取目標(biāo)P的靶標(biāo)中心,這兩個(gè)中心的圖像坐標(biāo)VAP、VBP為目標(biāo)P在不同相機(jī)里的成像位置,以該位置信息結(jié)合轉(zhuǎn)臺(tái)轉(zhuǎn)動(dòng)的角度信息計(jì)算光軸與兩臺(tái)相機(jī)光心連線的夾角,即水平角αAP、αBP,由式(1)可以求出該水平角。靶標(biāo)中心的縱坐標(biāo)與相機(jī)主點(diǎn)、焦距和像元尺寸聯(lián)合可求得靶標(biāo)中心的垂直角度βAP、βBP,由于線陣相機(jī)的主點(diǎn)和焦距為未知參數(shù),所以垂直角度βAP、βBP為未知參數(shù)。
1.3空間三維測(cè)量系統(tǒng)定向原理
由上述空間交會(huì)原理中式(3)、(4)可知,每個(gè)坐標(biāo)都與定向參數(shù)αAB、βAB、αBA以及b有關(guān),這些參數(shù)的精度直接影響特征點(diǎn)的空間坐標(biāo)的精度,因此,準(zhǔn)確測(cè)定這4個(gè)參數(shù)至關(guān)重要,這就是通常講的定向測(cè)量[7]。定向是指確定測(cè)站間的相互位置和方向,包括相對(duì)定向和絕對(duì)定向,相對(duì)定向指的是確定測(cè)站間的相互方位,絕對(duì)定向是指確定測(cè)站間的相互位置。
1.3.1相對(duì)定向
相對(duì)定向是用來確定起始方向,在本文中,全視角高精度采集儀A和B在同時(shí)觀測(cè)目標(biāo)P時(shí),由于在采集儀A和B上外貼標(biāo)志進(jìn)行互瞄時(shí),得到的αAB、βAB、αBA、βBA角度值不準(zhǔn)確,所以將這4個(gè)參數(shù)定為未知參數(shù),在測(cè)量平差中一同解算。
1.3.2絕對(duì)定向
由1.2節(jié)可知,全視角采集儀只能得到水平角度αAP、αBP和P點(diǎn)的像素坐標(biāo)VP(VAP、VBP)的值,無法進(jìn)行距離的測(cè)量,絕對(duì)定向?qū)嶋H上就是給出三維測(cè)量系統(tǒng)的尺度基準(zhǔn)——確定基線b的值,由于測(cè)距儀無法達(dá)到高的精度,若用激光干涉儀,雖具有高的測(cè)量精度,但在三維測(cè)量中很難實(shí)現(xiàn),所以,在三維測(cè)量系統(tǒng)中,通常用采集儀對(duì)某一基準(zhǔn)進(jìn)行觀測(cè)來反算采集儀之間的基線長(zhǎng)。由已知任意兩個(gè)靶標(biāo)的中心點(diǎn)距離d來確定基線的原理如圖2所示。
首先,A、B采集儀來完成相對(duì)定向,A、B互瞄時(shí),有未知參數(shù)αAB、βAB、αBA、βBA,然后A、B分別對(duì)任意兩個(gè)靶標(biāo)的中心點(diǎn)進(jìn)行觀測(cè),得到已知值αAPi、βAPi、αBPi、βBPi(i=1,2)。令:

依前方交會(huì)原理式(3)、(4)可得P1、P2兩點(diǎn)的空間坐標(biāo):
![FGC3C]}IFHE~J`{QJ`TSHMG.png FGC3C]}IFHE~J`{QJ`TSHMG.png](http://files.chinaaet.com/images/2017/04/07/6362715920809468762397995.png)
兩靶標(biāo)中心點(diǎn)的距離:
![DHVP_BM@G}_)VA%ZO@U18]1.png DHVP_BM@G}_)VA%ZO@U18]1.png](http://files.chinaaet.com/images/2017/04/07/6362715921642349304785162.png)
首先,由于未提前對(duì)線陣相機(jī)A進(jìn)行內(nèi)參標(biāo)定,所以此時(shí)V0A、fA為未知參數(shù)。由式(7)、(8)可知:在已知d、αAP、αBP、VP(VPi為VAP)的情況下,該方程有αAB、αBA、b、V0A、fA5個(gè)未知參數(shù)。在該方程中,由于式(8)為非線性方程組,則需在方程個(gè)數(shù)大于等于5的情況下,由牛頓迭代法把以上5個(gè)未知數(shù)求出。其次,由于未提前對(duì)線陣相機(jī)B進(jìn)行內(nèi)參標(biāo)定,所以此時(shí)V0B、fB為未知參數(shù)。由式(7)、(8)可知:在已知d、αAP、αBP、VP(VPi為VBP)的情況下,該方程有αAB、αBA、b、h、V0B、fB6個(gè)未知參數(shù)。在該方程中,則需在方程個(gè)數(shù)大于等于6的情況下,由牛頓迭代法把6個(gè)未知參數(shù)求出。最后,將上面兩次得到的αAB、αBA、b兩兩相加,取平均值,可以得到高精度的αAB,αBA,b。當(dāng)基線b以及采集儀A和B的高度差h確定時(shí),由式(5)可以求出βAB、βBA。此時(shí),所有未知參數(shù)b、h、αAB、βAB、αBA、βBA、V0A、fA、V0B、fB確定完畢,測(cè)量坐標(biāo)系也就建立起來了,即可以進(jìn)行三維測(cè)量。
2測(cè)量系統(tǒng)裝置構(gòu)建與測(cè)量流程
2.1測(cè)量系統(tǒng)裝置
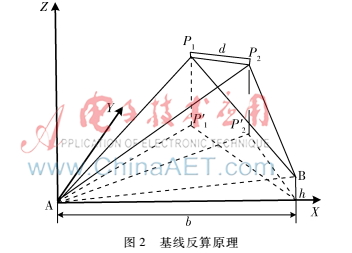
基于視覺測(cè)量技術(shù)的水平全視角高精度三維測(cè)量系統(tǒng)根據(jù)攝影測(cè)量原理,在測(cè)量場(chǎng)內(nèi)布置2臺(tái)全視角高精度數(shù)據(jù)采集儀,采集儀由兩臺(tái)相同的CMOS線陣相機(jī)以及高精度轉(zhuǎn)臺(tái)組成,測(cè)量系統(tǒng)裝置示意圖如圖3所示。
2.2測(cè)量總體流程
(1)使用兩套測(cè)量裝置,測(cè)量裝置連接安裝完畢,軟硬件已經(jīng)通過聯(lián)調(diào);
(2)布置測(cè)量場(chǎng),在測(cè)量場(chǎng)周圍安放足夠的靶標(biāo);
(3)將兩套測(cè)量裝置布放在測(cè)量場(chǎng)中央,并使它們具有一定距離,調(diào)節(jié)轉(zhuǎn)臺(tái),確定轉(zhuǎn)臺(tái)零度角位置;
(4)設(shè)定相機(jī)的工作參數(shù)(采樣頻率、曝光時(shí)間等)、轉(zhuǎn)臺(tái)的工作參數(shù)(轉(zhuǎn)速、觸發(fā)脈沖的頻率等);
(5)啟動(dòng)相機(jī)和轉(zhuǎn)臺(tái)進(jìn)行水平全視角掃描并實(shí)時(shí)使用圖像采集卡采集圖像數(shù)據(jù);
(6)對(duì)獲取的圖像進(jìn)行靶標(biāo)提取,得到靶標(biāo)像素;
(7)利用靶標(biāo)中心,結(jié)合轉(zhuǎn)臺(tái),求解靶標(biāo)中心對(duì)應(yīng)的水平角度;
(8)由第1節(jié)求解三維坐標(biāo)信息并平差優(yōu)化。
3測(cè)量系統(tǒng)實(shí)驗(yàn)測(cè)試
3.1仿真數(shù)據(jù)
在該仿真試驗(yàn)中,假設(shè)被測(cè)大尺寸物體為一個(gè)平面,已知平面上有9個(gè)靶標(biāo),以采集儀A中線陣相機(jī)光心為空間坐標(biāo)系原點(diǎn),其各靶標(biāo)的中心點(diǎn)空間坐標(biāo)如下表1所示。
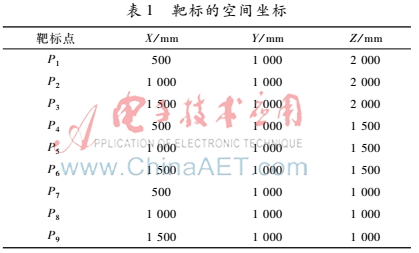
在已知各靶標(biāo)中心點(diǎn)的空間坐標(biāo)時(shí),可以計(jì)算得到任意兩個(gè)靶標(biāo)中心點(diǎn)的空間距離d,在本文中,假設(shè)轉(zhuǎn)臺(tái)A的起始角度α0A=800,轉(zhuǎn)臺(tái)B的起始角度α0B=400,Δb=7.04 μm,αAB=1800,βAB=0.477 5°,αBA=00,βBA=89.522 5,b=6 mm,h=50 mm,V0A=4 096,fA=60 mm,V0B=4 096,fB=60 mm。當(dāng)全視角高精度數(shù)據(jù)采集儀A、B從兩個(gè)不同視角掃描同一個(gè)靶標(biāo)時(shí),其仿真模型裝置如圖3所示,在已知各靶標(biāo)中心點(diǎn)的空間坐標(biāo)以及b、h、αAB、βAB、αBA、βBA、V0A、fA、V0B、fB的值時(shí),由靶標(biāo)中心點(diǎn)的空間三角函數(shù)關(guān)系式以及式(2)、(3),可以快速地求出靶標(biāo)面上9個(gè)靶標(biāo)中心點(diǎn)的αAP、βAP、αBP、βBP的角度以及像素坐標(biāo)值VPA、VPB。
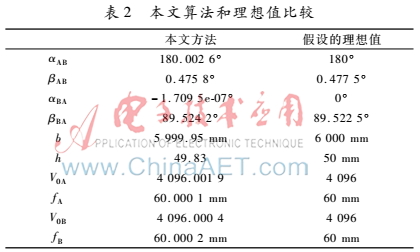
在全視角高精度三維測(cè)量系統(tǒng)中,全視角高精度采集儀A和B采集到的數(shù)據(jù)中,在已知d、αAP、βAP、VPA的情況下,由式(7)、(8)可以求出采集儀A的未知參數(shù)αAB、βAB、b、V0A、fA。同理,在已知d、αBP、βBP、VPB的情況下,可以求出采集儀B的未知參數(shù)αAB、βAB、b、h、V0B、fB,由式(5)求出βAB、βBA。所求參數(shù)的值如表2所示。
3.2真實(shí)數(shù)據(jù)

全視角高精度三維測(cè)量系統(tǒng)中,采用TELEDYNE DALSA公司的Piranha4 8K Camera (P4-CC-08K050-00-R)線陣相機(jī),主要參數(shù)如表3所示。表3線陣相機(jī)主要參數(shù)名稱參數(shù)值分辨率/pixels8192像素單元尺寸/(μm)27.04×7.04采樣頻率/kHz≥20曝光時(shí)間/μs>50控制和數(shù)據(jù)接口CameraLink Full電源接口Hirose電源電壓12 V~24 VDC
被測(cè)靶標(biāo)平面中靶標(biāo)的實(shí)際排列位置如圖4(a)所示。其三維測(cè)量掃描裝置如圖4(b)所示。
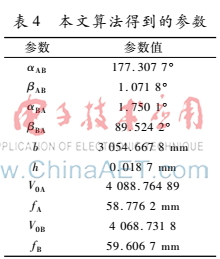
圖4中,轉(zhuǎn)臺(tái)A的起始角度α0A=800,轉(zhuǎn)臺(tái)B的起始角度α0B=400,每列像素對(duì)應(yīng)的旋轉(zhuǎn)角度圖4空間靶標(biāo)板平面及其三維測(cè)量掃描裝置Δα=0.007 50,由表3可知,像元尺寸Δb=7.04 μm。在已知靶標(biāo)中心點(diǎn)像素坐標(biāo)的條件下,由式(1)計(jì)算兩個(gè)測(cè)量裝置掃描靶標(biāo)時(shí)采集一次圖像的旋轉(zhuǎn)水平角度αAP、αBP,接下來由人為直接測(cè)量P1~P16中任意兩個(gè)靶標(biāo)的實(shí)際距離d,將測(cè)量裝置掃描靶標(biāo)時(shí)采集一次圖像的旋轉(zhuǎn)水平角度αAP、αBP以表4本文算法得到的參數(shù)參數(shù)參數(shù)值αAB177.307 7°βAB1.071 8°αBA1.750 1°βBA89.524 2°b3 054.667 8 mmh0.018 7 mmV0A4 088.764 89fA58.776 2 mmV0B4 068.731 8fB59.606 7 mm及d帶入式(7)、(8),可以求出采集儀A的未知參數(shù)αAB、βAB、b、V0A、fA,以及采集儀B的未知參數(shù)αAB、βAB、b、h、V0B、fB。求出未知參數(shù)如表4所示。

將表4中求出的參數(shù)帶入式(7)中,以采集儀A中線陣相機(jī)光心為空間坐標(biāo)系原點(diǎn),用表5中的坐標(biāo)算出P1~P16中部分任意兩個(gè)靶標(biāo)的實(shí)際距離d,如表5所示。

4結(jié)論
本文基于全視角高精度三維測(cè)量系統(tǒng)在測(cè)量過程中采用兩臺(tái)測(cè)量裝置進(jìn)行測(cè)量,采用以掃描速度等于其旋轉(zhuǎn)速度的方式進(jìn)行圖像的采集,從而保證了后續(xù)計(jì)算靶標(biāo)中心空間坐標(biāo)的精度。本文不僅解決了電子經(jīng)緯儀測(cè)量精度不高、自動(dòng)程度低以及面陣相機(jī)圖像分辨率受限等問題,同時(shí)解決了傳統(tǒng)基于計(jì)算機(jī)視覺測(cè)量技術(shù)的三維測(cè)量系統(tǒng)不能實(shí)現(xiàn)全視角(水平360°)測(cè)量的問題,實(shí)現(xiàn)了水平全視角圖像采集的不失真。同時(shí)采用非接觸式測(cè)量,測(cè)量范圍大、精度高,具有良好的實(shí)用價(jià)值。
參考文獻(xiàn)
[1] 黃桂平,欽桂勤,盧成靜.數(shù)字近景攝影大尺寸三坐標(biāo)測(cè)量系統(tǒng)V-STARS的測(cè)試與應(yīng)用[J].宇航計(jì)測(cè)技術(shù),2009,29(2):5-9.
[2] 李廣云.工業(yè)測(cè)量系統(tǒng)最新進(jìn)展及應(yīng)用[J].測(cè)繪工程,2001,10(2):36-40.
[3] 戴相龍.三維非接觸式測(cè)量中編碼標(biāo)志的研究與應(yīng)用[D].西安:西安電子科技大學(xué),2014.
[4] 黃桂平.數(shù)字近景工業(yè)攝影測(cè)量關(guān)鍵技術(shù)研究與應(yīng)用[D].天津:天津大學(xué),2005.
[5] 張旭蘋,汪家其,張益昕,等. 大尺度三維幾何尺寸立體視覺測(cè)量系統(tǒng)實(shí)現(xiàn)[J].光學(xué)學(xué)報(bào),2012,32(3):140-147.
[6] 趙立,王佩賢,張貴豪. 基于T3000電子經(jīng)緯儀的工業(yè)測(cè)量系統(tǒng)及其精度分析[C]. 第二屆中國(guó)衛(wèi)星導(dǎo)航學(xué)術(shù)年會(huì)CSNC,2011.
[7] 張益昕.基于計(jì)算機(jī)視覺的大尺度三維幾何尺寸測(cè)量方法及應(yīng)用[D].南京:南京大學(xué),2011.

