陳德華,洪靈濤,潘喬
(東華大學 計算機科學與技術學院,上海 201620)
摘要:糖尿病在治療過程中,其生化檢驗指標的變化受患者基本特征、指標等影響。文中針對預測患者糖尿病生化指標的問題,結合神經(jīng)網(wǎng)絡等機器學習方法,構建了一個基于改進神經(jīng)網(wǎng)絡的糖尿病生化指標預測模型。該模型考慮了糖尿病生化指標和患者的基本特征對指標的影響,同時又將患者之前的檢驗數(shù)據(jù)樣本加入到模型中。實驗證明,對于糖尿病患者的指標數(shù)據(jù),3個主要血檢指標預測訓練集的R2值達到0.772 1、0.551 8、0.706 3,測試集的R2值達到了0.644 7、0.584 0、0.804 6,對比實驗也證明了該模型相較于常用的機器學習模型有著更好的預測效果。
關鍵詞:糖尿病;神經(jīng)網(wǎng)絡;指標預測
中圖分類號:TP302文獻標識碼:ADOI: 10.19358/j.issn.1674-7720.2017.05.017
引用格式:陳德華,洪靈濤,潘喬.基于改進神經(jīng)網(wǎng)絡的糖尿病生化指標值預測[J].微型機與應用,2017,36(5):54-56,59.
0引言
糖尿病作為一個高發(fā)的內分泌疾病,其各項指標的預測都有很重要的意義。糖化血紅蛋白(HbA1c) 指標是人體血液中紅細胞內的血紅蛋白與血糖結合的產(chǎn)物, 通常可以反映患者近8~12周的血糖控制情況;空腹血糖(Glu)指標能夠代表基礎胰島素的分泌功能;而胰島素釋放試驗(Ins)反應了胰β細胞的儲備功能,這些糖尿病的主要指標預測具有調整治療方案、評估患者狀態(tài)、衡量治療結果等重要的實際意義。
以往糖尿病的指標預測僅僅停留在醫(yī)學領域或者簡單的統(tǒng)計分析上。隨著機器學習技術的發(fā)展,各類機器學習模型也被應用到醫(yī)療行業(yè)的各個領域。但是對于大量有不同特性的數(shù)據(jù)樣本,許多機器學習的模型過于泛用,而對于糖尿病指標數(shù)據(jù)的預測而言,以往的模型大多停留在解決指標間的相關性上,而沒有考慮到患者一直以來的指標變化。同時患者指標變化數(shù)據(jù)具有不規(guī)則時序特性,這些特性也阻礙了一些模型應用到這類特殊的數(shù)據(jù)集上。
本文提出了一個基于改進神經(jīng)網(wǎng)絡的模型,該模型不僅充分考慮到患者指標間的相互影響,同時通過加入隱藏層來擬合患者多次檢查中不規(guī)則的時序特性,對比實驗也證明了該模型相較于常用的機器學習模型有著更好的預測效果。
1糖尿病臨床數(shù)據(jù)建模
糖尿病臨床數(shù)據(jù)主要由兩部分組成:患者的基本信息,此維數(shù)據(jù)主要包括了患者的性別、年齡、妊娠狀態(tài)等;患者的檢驗數(shù)據(jù),此維數(shù)據(jù)主要包括了患者歷次的各項生化指標的檢驗時間和指標值。
由以上兩類數(shù)據(jù)源可以得到一個以患者、時間和患者屬性(包括患者特征和指標等)為3個維度的三維數(shù)據(jù)模型,而這個數(shù)據(jù)模型有以下特點:
(1)不規(guī)則的時序特性
例1.表1中列舉了一個患者血液檢查中糖尿病主要指標的數(shù)據(jù)樣本。該數(shù)據(jù)的時間跨度從2011年~2012年,共有5次檢查數(shù)據(jù),每次檢查與上一次檢查的時間間隔分別為110天、103天、128天和60天。
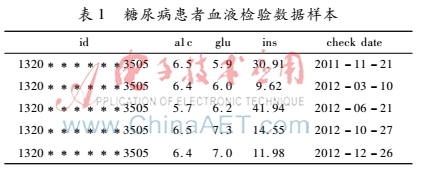
例1中可以看到,醫(yī)療數(shù)據(jù)的確具有時序特性,但相較于標準的或者較為正規(guī)的時序數(shù)據(jù)集,醫(yī)療數(shù)據(jù)的時序點更為殘缺和稀疏。這就使得很多數(shù)學模型并不適用于真實醫(yī)療數(shù)據(jù)的預測。
(2)指標和患者基本信息具有相關性
例2. 表2為不同性別分組A1C指標的統(tǒng)計描述。展示了不同年齡和性別分組的情況下患者的A1C指標分布情況。從例2中可以看出,不同性別的患者指標分布并不均勻,同時患者的年齡對指標的分布也有著影響。
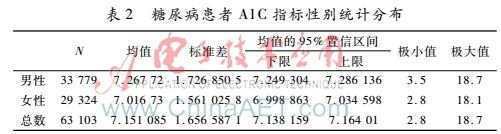
(3)指標間具有相關性
患者的指標存在相互影響的關系,相關資料也表明,患者的疾病指標也與很多的患者特性有著諸多相關,所以指標間的相互影響不可忽略。
2神經(jīng)網(wǎng)絡及存在的不足
BP神經(jīng)網(wǎng)絡[1 2]是一種按誤差逆?zhèn)鞑ニ惴ㄓ柧毜亩鄬忧梆伨W(wǎng)絡,是目前應用最廣泛的神經(jīng)網(wǎng)絡模型之一。神經(jīng)網(wǎng)絡擅長于處理內部機制復雜的問題,具有較強的非線性映射能力,因而神經(jīng)網(wǎng)絡在處理指標間、患者基本屬性與指標預測的關系時有較強的能力[3]。但是,由于需要同時考慮到患者多次檢查對患者指標的影響,一般的神經(jīng)網(wǎng)絡無法處理多次輸入之間的關系,不能很好地適應當前的數(shù)據(jù)模型。因而為了較好地預測糖尿病患者的幾個主要指標變化,提高預測精確度,本文利用糖尿病患者特征、治療時間和治療過程中的指標變化特性,提出了一個基于神經(jīng)網(wǎng)絡的改進神經(jīng)網(wǎng)絡模型,利用了BP神經(jīng)網(wǎng)絡[2 3]中的思想,來完成糖尿病指標的預測。
3預測模型架構
根據(jù)上節(jié)的描述,考慮到患者的各種特征對指標預測的影響,將患者性別、年齡、妊娠狀態(tài)等也作為模型的輸入。同時,如例1種所述,考慮到醫(yī)療數(shù)據(jù)所具有的時序特性,本文在改進的模型中加入了一個隱藏層,用于保存上一次隱層的輸出,并將它用于下一次的隱層計算,以此來擬合醫(yī)療數(shù)據(jù)的時序特性。為了簡化部分計算,減低模型可能的過擬合概率,模型將一些與預測結果直接相關的輸入單獨列出,作為特殊的節(jié)點輸入,直接連接到輸出節(jié)點。
3.1模型描述
實驗中的模型是基于BP神經(jīng)網(wǎng)絡改進的,具體包括4個層次,即輸入層、隱藏層1、隱藏層2和輸出層次。
將輸入?yún)?shù)x1,x2,…,xn記作x,對輸入?yún)?shù)先進行線性變換,對于隱層1節(jié)點j的輸入有:

其中ωTj表示連接輸入層和隱層1節(jié)點j的權值向量,ωi→j表示輸入層節(jié)點i到隱層j的權值,n表示輸入層節(jié)點數(shù)量。
隱層中激勵函數(shù)選用sigmoid函數(shù),所以為了保證sigmoid有較好的感知效果,本文利用sigmoid在定義域為0附近較為敏感的特性,結合數(shù)據(jù)特點,將式(1)中的kj進行雙曲變換,然后再附上偏置量,由此得到隱層的激勵函數(shù)為:
![_@{S43L}}EC`[6S]2A[OYG5.png _@{S43L}}EC`[6S]2A[OYG5.png](http://files.chinaaet.com/images/2017/04/07/6362716384665684358787926.png)
其中pi表示隱層1節(jié)點i的輸出,βi為對應偏置量。
隱層2的節(jié)點i保存著上一次隱層1節(jié)點的輸出,將隱層的節(jié)點i輸出記作yi,隱層2的節(jié)點i所保存的值記作y′i(注:隱層1、2的節(jié)點數(shù)相同),則對于隱層節(jié)點i的實際輸出有:
yi=pi+αiy′i(3)
其中αi表示隱層2節(jié)點i所對應的輸出權值。
對于輸入層中包含特殊節(jié)點N,筆者認為在這樣一份時序數(shù)據(jù)中,每條數(shù)據(jù)的時間與其輸出有直接關系,則不將該節(jié)點通過隱層處理,而是直接連接到輸出層。將隱層的輸出y1,y2,…,yn記作y,在輸出層采用purelin函數(shù),可以得到輸出層的輸出zj為:
zj=υTj·y+γj·g+bj=∑m1υi→j·yi+γj·g+bj(4)
其中υTj表示連接隱層和輸出層節(jié)點j的權值向量,υi→j表示隱層節(jié)點i到輸出層節(jié)點j的權值,bj表示對應偏置量,m為隱層節(jié)點數(shù)量,g表示特殊節(jié)點輸入值,γj為對應權值。
3.2學習過程
整個訓練過程基本采用BP算法的思想,首先,模型的整體MSE為:
![4HED[]DK@]6_G[QIV3}K]AV.png 4HED[]DK@]6_G[QIV3}K]AV.png](http://files.chinaaet.com/images/2017/04/07/6362716386612717967363517.png)
其中rj 為預測結果的實際值。為后續(xù)計算方便,這里添加了系數(shù)12。
訓練學習過程以最小化MSE為目的,利用梯度下降算法,以目標負梯度方向對參數(shù)進行調整,對于誤差函數(shù)(5)和給定學習率η,參數(shù)ωi→j的負梯度變化量為:
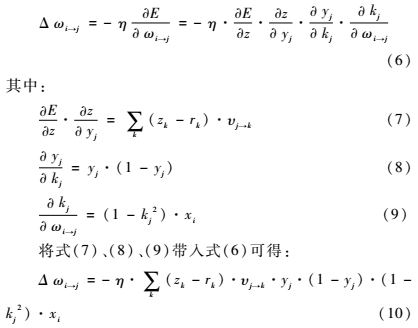
同理,根據(jù)式(10)同樣的推導方式可以得到其他參數(shù)的變化量為:
![Y2U{`})$9J]}V~}~4QDJACE.png Y2U{`})$9J]}V~}~4QDJACE.png](http://files.chinaaet.com/images/2017/04/07/6362716388528499244792652.png)

4實驗評估
本實驗中的醫(yī)療數(shù)據(jù)源于國內某大型三甲醫(yī)院的糖尿病患者的醫(yī)療數(shù)據(jù)。共有348位患者的信息,每個患者至少包括了3條以上的檢查數(shù)據(jù)。共1 399條檢查數(shù)據(jù)。數(shù)據(jù)以7:3的比例劃分訓練集和測試集。模型的輸出為預測時間下的A1C、GLU、INS 3個指標的值。
4.1模型評價標準和參數(shù)設定

首先對模型的數(shù)值數(shù)據(jù)進行歸一化處理。本節(jié)選取均方誤差(Mean Square Error, MSE)和決定系數(shù)(coefficient of determination, R2)來作為實驗的評價指標。兩者的計算公式如下:
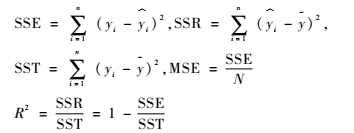
后續(xù)實驗均選取R2來衡量實驗結果。
圖1給出了在不同BP迭代次數(shù)的情況下模型的R2值。可以看到,當BP的迭代次數(shù)大于500次時,模型預測結果的R2值已經(jīng)基本保持不變。所以本文實驗中對于每一次BP過程,每一個參數(shù)迭代500次或迭代至該參數(shù)收斂為止。

實驗時模型采用動態(tài)學習率,學習率在每一個新樣本進入模型時更新,學習率公式為:
![VV_J$V1]Q@7LF$~U72`K`2K.png VV_J$V1]Q@7LF$~U72`K`2K.png](http://files.chinaaet.com/images/2017/04/07/6362716390325520559174020.png)
其中,η′為上一個樣本時模型的學習率。本系列實驗中學習率的初始值為0.05。
4.2實驗結果評估
在上述實驗條件下,經(jīng)過100次隨機初值實驗獲得3個指標值預測結果的R2均值。實驗可以看出,該模型對于本數(shù)據(jù)集的預測效果較好,無論是訓練集還是測試集的決定系數(shù)R2都在0.6~0.8左右,模型的擬合程度較好。
實驗過程中進行了對比實驗,對比實驗中使用了普通的BP神經(jīng)網(wǎng)絡、xgboost等算法對相同的數(shù)據(jù)進行了預測,在表4中可見各個算法的對指標預測的R2值。在對比實驗結果中可以看到,本文提出的模型總體的表現(xiàn)最好; xgboost在測試集表現(xiàn)與本文提出的模型相近,但是迭代次數(shù)在20次時就已過擬合。而一般的神經(jīng)網(wǎng)絡模型擬合的效果較差,并不能達到良好的預測效果。
5結論
本文提出了一個基于BP神經(jīng)網(wǎng)絡,針對糖尿病醫(yī)療數(shù)據(jù)集所構建的改進神經(jīng)網(wǎng)絡預測模型。與一般的神經(jīng)網(wǎng)絡相比,該模型針對于特定數(shù)據(jù)集,添加了隱層用來保存上一次隱層節(jié)點的輸出,修改了隱層的激勵函數(shù),加入了特殊節(jié)點來更好地擬合數(shù)據(jù)。在第四節(jié)的實驗中,可以看到本文所構建的模型對于糖尿病的醫(yī)療數(shù)據(jù)集的預測有良好的表現(xiàn)。在預測準確性上,要優(yōu)于傳統(tǒng)的神經(jīng)網(wǎng)絡及其他的模型。
參考文獻
[1] Cai Binghuang, Jiang X. A novel artificial neural network method for biomedical prediction based on matrix pseudo-inversion[J]. Journal of Biomedical Informatics, 2014, 48(3):114-121.
[2] PAPPADA S M, CAMERON B D, ROSMAN P M, et al. Neural network based real time prediction of glucose in patients with insulin-dependent diabetes[J]. Diabetes Technology & Therapeutics, 2011, 13(2):13541.
[3] WYSOCKI, LAWRYN'CZUK A, MACIEJ. Elman neural network for modeling and predictive control of delayed dynamic systems[J]. Archives of Control Sciences, 2016, 26(1):117 142.
[4] RODRIGUEZ P, WILES J, ELMAN J L. A recurrent neural network that learns to count[J]. Connection Science, 1999, 11(1):540.

