于一丁,王永川,王長(zhǎng)龍

　　（軍械工程學(xué)院 無(wú)人機(jī)工程系,，河北 石家莊 050003）

        摘要：為了分析基于多值量化的混沌擴(kuò)頻序列的性能,，以Chebyshev混沌映射為例，結(jié)合其概率密度分布函數(shù)的特點(diǎn)給出對(duì)其進(jìn)行多值量化的方法,。仿真分析多值量化混沌序列的平衡性和相關(guān)性,，在高斯白噪聲信道中對(duì)傳統(tǒng)二值量化混沌序列和多值量化混沌序列擴(kuò)頻通信系統(tǒng)進(jìn)行誤碼率仿真，并從低檢測(cè)概率和低利用概率兩個(gè)角度對(duì)多值量化混沌序列的抗截獲性能進(jìn)行分析,。仿真結(jié)果表明多值量化混沌序列的誤碼率性能更好,，其抗截獲性能也有所提高。

　　關(guān)鍵詞：混沌序列,；多值量化,；抗截獲

　　中圖分類號(hào)：TN914文獻(xiàn)標(biāo)識(shí)碼：ADOI： 10.19358/j.issn.1674-7720.2017.06.018

　　引用格式：于一丁,王永川,王長(zhǎng)龍. 基于多值量化的混沌擴(kuò)頻序列及其性能分析［J］.微型機(jī)與應(yīng)用，2017,36（6）：58-61.

0引言

　　*基金項(xiàng)目：裝備預(yù)研基金項(xiàng)目（9140A25031314JB34004）混沌現(xiàn)象是非線性動(dòng)態(tài)系統(tǒng)中出現(xiàn)的確定性的類隨機(jī)過(guò)程,這種過(guò)程具備高度的初值敏感性,非周期又不收斂,。通過(guò)混沌映射可以生成大量具有尖銳自相關(guān)性,、近似正交互相關(guān)性、類噪聲的混沌序列［1］,。相比傳統(tǒng)的擴(kuò)頻序列如m序列,、Gold序列等，混沌序列具有更好的偽隨機(jī)性,、更高的復(fù)雜度和抗截獲能力,，更加適合作為擴(kuò)頻碼應(yīng)用到擴(kuò)頻通信系統(tǒng)中［2］。

　　目前針對(duì)混沌序列的生成和優(yōu)選方法國(guó)內(nèi)外已經(jīng)做過(guò)大量研究［35］,，但仍存在一些問(wèn)題：由混沌映射生成的混沌序列通常要經(jīng)過(guò)數(shù)字量化處理后才能應(yīng)用于擴(kuò)頻通信系統(tǒng)中,，目前對(duì)混沌序列通常采用二值化處理，常用的方法有門限量化法［6］,、比特抽取量化法［7］,、中值量化法［8］等，但在二值化的過(guò)程中混沌序列會(huì)損失大量信息,。為了改善混沌擴(kuò)頻序列的性能,，本文將多值量混沌序列作為擴(kuò)頻碼應(yīng)用于擴(kuò)頻通信系統(tǒng)中,，以Chebyshev混沌映射為例，將傳統(tǒng)二值量化混沌序列和多值量化混沌序列應(yīng)用于直接序列擴(kuò)頻（DSSS）系統(tǒng)中并進(jìn)行仿真,，仿真結(jié)果表明多值量化混沌擴(kuò)頻序列的性能優(yōu)于傳統(tǒng)的二值量化混沌擴(kuò)頻序列,，更加符合擴(kuò)頻通信系統(tǒng)的要求。

1混沌擴(kuò)頻通信系統(tǒng)

　　混沌擴(kuò)頻通信系統(tǒng)的基本原理和傳統(tǒng)直接序列擴(kuò)頻系統(tǒng)類似,，只是將偽隨機(jī)序列換成混沌序列,，其基本原理是將信源數(shù)據(jù)用混沌序列進(jìn)行擴(kuò)頻調(diào)制，調(diào)制之后信源數(shù)據(jù)的頻譜被擴(kuò)展并通過(guò)天線傳入信道,，在接收端則采用與發(fā)送端同步的混沌序列進(jìn)行相關(guān)解擴(kuò)恢復(fù)數(shù)據(jù),。圖1為混沌擴(kuò)頻通信系統(tǒng)框圖。

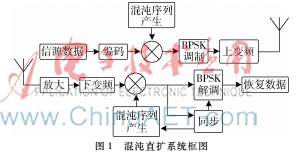
　　混沌擴(kuò)頻通信系統(tǒng)采用混沌序列作為擴(kuò)頻碼,，充分利用了混沌序列數(shù)量眾多,、偽隨機(jī)性良好、序列復(fù)雜度高等優(yōu)勢(shì),，提高了直擴(kuò)系統(tǒng)的可靠性和安全性,。

2混沌序列的多值量化

　　混沌序列一般通過(guò)非線性混沌映射反復(fù)迭代產(chǎn)生，常見(jiàn)的混沌映射有Logistic映射,、Chebyshev映射,、Tent映射等。本文以Chebyshev混沌映射作為模型進(jìn)行研究,，其映射公式為：

　　xn+1=f(x)=cos(ωarccosxn)(1)

　　初始值x0∈(－1,1),，ω為映射的階數(shù)，當(dāng)ω=2n時(shí),，系統(tǒng)處于混沌狀態(tài),，其概率密度分布函數(shù)為：

　　混沌序列應(yīng)用于擴(kuò)頻通信系統(tǒng)中通常需要經(jīng)過(guò)數(shù)值量化處理，相比于常規(guī)的二值量化,，經(jīng)過(guò)多值量化處理后的序列混沌特性損失減小,，序列復(fù)雜度更高，偽隨機(jī)性更強(qiáng),，有利于提升擴(kuò)頻通信系統(tǒng)的性能,。下面對(duì)混沌序列多值量化的方法進(jìn)行分析。

　　假設(shè)對(duì)混沌序列進(jìn)行N值量化,，則需要通過(guò)N+1個(gè)劃分點(diǎn)將區(qū)間 ［-1,1］ 劃分成N段連續(xù)的子區(qū)間,，劃分點(diǎn)設(shè)為a0,a1，…,aN+1,，其中a0=－1,aN+1=1,。為了保證N值量化的均勻性，要求混沌序列在每個(gè)子區(qū)間上的分布概率相同,，由式（2）可知Chebyshev混沌映射在子區(qū)間［ak,ak+1］上的分布概率為：

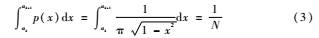
　　可得

　　ak=－cos(kπ/N) ,k=0,1,2,…,N(4)

　　由于改進(jìn)型Logistic混沌映射同Chebyshev混沌映射具有相同的概率密度分布函數(shù),，因此文中給出的多值量化方法也同樣適用于改進(jìn)型Logistic混沌映射,。

3多值量化混沌序列性能分析

　　3.1平衡性

　　混沌序列的平衡性與載波抑制度有密切的關(guān)系，低平衡性的混沌序列會(huì)導(dǎo)致直擴(kuò)系統(tǒng)的載漏增大,，將破壞擴(kuò)頻系統(tǒng)保密性,、抗干擾和抗偵破的能力。二值量化序列的平衡度E為：

　　E=|U－V|/L（5）

　　式中U與V分別表示混沌序列中1與-1的數(shù)目,，L表示序列長(zhǎng)度。鑒于二值量化平衡度公式不適用于衡量多值量化序列的平衡性,，本文采用一種新指標(biāo)來(lái)替代E對(duì)多值量化序列的平衡性進(jìn)行衡量,。對(duì)于多值量化序列，定義其平衡指數(shù)：

　　rn=|un－1/N|（6）

　　定義最大平衡指數(shù)：

　　rmax=|umax－1/N|max（7）

　　式中1/N代表多值量化混沌序列中每種量化值應(yīng)占的理想比例,，un代表一種量化值在整個(gè)擴(kuò)頻序列中所占的百分比,。最大平衡指數(shù)表征了整個(gè)序列平衡性的最大差異，最大平衡指數(shù)越接近零,，代表序列的整體平衡性能越好,，下面通過(guò)仿真對(duì)二值量化序列和多值量化的最大平衡指數(shù)進(jìn)行分析。仿真條件：N=4,，對(duì)混沌序列進(jìn)行四值量化,，量化值設(shè)為±1、±2,，觀察最大平衡指數(shù)隨著序列長(zhǎng)度增加的變化趨勢(shì),，仿真結(jié)果如圖2所示。從圖中可以看出兩種量化方法均具有良好的平衡性,，當(dāng)序列長(zhǎng)度大于1 000時(shí),，最大平衡指數(shù)的數(shù)值曲線趨于平穩(wěn)并接近于零，這證明了本文采用的量化方法是可行的,，可以確保多值量化序列擁有良好的平衡性,。

　　3.2相關(guān)性

　　相關(guān)性是衡量擴(kuò)頻序列性能的重要指標(biāo)，與擴(kuò)頻通信系統(tǒng)的抗干擾能力和抗多址能力密切相關(guān),。理想的擴(kuò)頻序列應(yīng)該具備類似白噪聲一樣尖銳的自相關(guān)函數(shù)和處處為零的互相關(guān)函數(shù)［9］,。設(shè){x}和{y}是周期為L(zhǎng)的兩個(gè)混沌序列，則{x}與{y}的互相關(guān)函數(shù)Rxy(m)定義為：

　　m為兩個(gè)序列間的相關(guān)間隔,，定義序列{x}的自相關(guān)函數(shù)Rx(m)為：

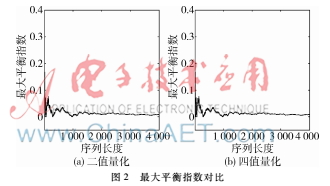
　　圖3和圖4給出了二值量化和多值量化后混沌序列的自相關(guān)函數(shù)曲線和互相關(guān)函數(shù)曲線,。從圖中可以看出多值量化混沌序列相關(guān)特性良好，其自相關(guān)函數(shù)有尖銳的相關(guān)峰,，互相關(guān)函數(shù)值非常小,，幾乎接近于零。同二值量化混沌序列相比多值量化混沌序列的互相關(guān)性能差別不大,其自相關(guān)函數(shù)有更大的相關(guān)峰值,，有利于合作通信方對(duì)擴(kuò)頻信號(hào)的檢測(cè)以及同步過(guò)程中對(duì)擴(kuò)頻序列的捕獲識(shí)別,。

　　3.3誤碼率性能分析

　　為了進(jìn)一步驗(yàn)證多值量化混沌擴(kuò)頻序列的性能,，將其作為擴(kuò)頻碼應(yīng)用到直接序列擴(kuò)頻系統(tǒng)中并進(jìn)行仿真，為保證結(jié)果的準(zhǔn)確性和可靠性,，采用蒙特卡羅方法進(jìn)行仿真,，考慮到平衡性要求，仿真過(guò)程中設(shè)定混沌擴(kuò)頻序列長(zhǎng)度為1 000,，默認(rèn)碼元速率為1,，調(diào)制方式為BPSK，系統(tǒng)信道為高斯白噪聲信道（AWGN）,，信噪比取值范圍是［-20 dB,，10 dB］，為了進(jìn)一步驗(yàn)證多值量化對(duì)系統(tǒng)誤碼率的影響,，仿真過(guò)程中補(bǔ)充加入八值量化混沌擴(kuò)頻序列進(jìn)行對(duì)比分析,，仿真結(jié)果如圖5所示。

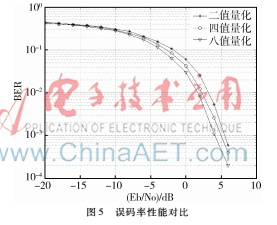
　　從圖5中可以看出多值量化序列在AWGN信道下的誤碼率性能好于二值量化混沌序列,，八值量化序列的誤碼率性能優(yōu)于四值量化序列,，其原因在于多值量化在一定程度上彌補(bǔ)了擴(kuò)頻序列混沌特性的損失，序列的隨機(jī)性和復(fù)雜度均有所提升,。仿真結(jié)果表明多值量化混沌擴(kuò)頻序列可以有效提高擴(kuò)頻系統(tǒng)的可靠性,，降低信號(hào)傳輸?shù)恼`碼率，更適用于擴(kuò)頻通信系統(tǒng),。

　　3.4抗截獲性能分析

　　抗截獲性能是衡量通信系統(tǒng)可靠性,、安全性的重要指標(biāo)。本文從低檢測(cè)概率（LPD）和低利用概率（LPE）兩個(gè)角度對(duì)多值量化混沌擴(kuò)頻序列的抗截獲性能進(jìn)行分析,。

　　直擴(kuò)通信的LPD性能指的是直擴(kuò)信號(hào)被非合作方截獲接收機(jī)發(fā)現(xiàn)的性能,。對(duì)于一組擴(kuò)頻序列{xn}定義:

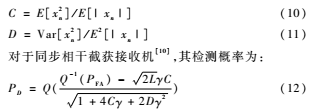
　　式中γ是截獲接收機(jī)接收端擴(kuò)頻信號(hào)的信噪比，L是截獲接收機(jī)一次觀察的切普數(shù),，PFA為虛警概率,。仿真參數(shù)設(shè)定PFA=0.01，L=1 000,。多值量化序列的檢測(cè)概率PD隨γ的變化情況如圖6所示,。

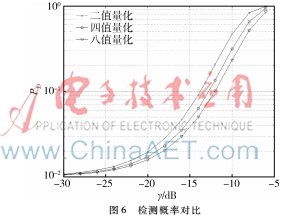
　　圖7抗截獲誤碼率對(duì)比從圖6中可以看出經(jīng)過(guò)八值量化的擴(kuò)頻信號(hào)的檢測(cè)概率最低，四值量化次之,，二值量化擴(kuò)頻信號(hào)的檢測(cè)概率最高,。仿真結(jié)果表明多值量化混沌序列可以降低擴(kuò)頻信號(hào)的檢測(cè)概率，提高系統(tǒng)的LPD性能,。

　　直擴(kuò)通信的LPE性能指的是直擴(kuò)信號(hào)被敵方接收機(jī)截獲后,，其攜帶的信息和情報(bào)被還原和獲取的能力。相對(duì)于二值量化混沌序列，多值量化混沌序列的系統(tǒng)動(dòng)力學(xué)特性更加復(fù)雜,系統(tǒng)的參數(shù)變量更多,，即使敵方接收機(jī)檢測(cè)到我方擴(kuò)頻信號(hào),，甚至分析出擴(kuò)頻序列碼長(zhǎng)、碼元速率等系統(tǒng)參數(shù),，在不清楚我方混沌擴(kuò)頻序列多值量化規(guī)則的情況下也難以對(duì)信號(hào)攜帶的信息情報(bào)進(jìn)行還原,。敵方在檢測(cè)到我方直擴(kuò)信號(hào)后經(jīng)過(guò)常規(guī)二值相關(guān)解擴(kuò)得到的誤碼率仿真曲線如圖7所示。

　　從圖7中可以看出經(jīng)過(guò)四值量化混沌擴(kuò)頻序列調(diào)制過(guò)的信號(hào)誤碼率失真嚴(yán)重,，經(jīng)過(guò)八值量化混沌擴(kuò)頻序列調(diào)制的信號(hào)幾乎完全失真,。仿真結(jié)果表明經(jīng)過(guò)多值量化后的混沌擴(kuò)頻序列LPE性能更好，有利于提高通信系統(tǒng)的可靠性和安全性,。

　4結(jié)論

　　本文研究了對(duì)混沌序列進(jìn)行多值量化的方法,，分析了多值量化混沌擴(kuò)頻序列的平衡性、相關(guān)性等性能,，并將其作為擴(kuò)頻碼應(yīng)用到直接序列擴(kuò)頻通信系統(tǒng)中進(jìn)行仿真，仿真結(jié)果表明多值量化擴(kuò)頻序列擁有良好的平衡性和相關(guān)性,，經(jīng)過(guò)多值量化序列調(diào)制后的信號(hào)在AWGN信道中可獲得更好的誤碼率性能,，抗截獲性能也有所提高，基于多值量化的混沌擴(kuò)頻序列更適用于擴(kuò)頻通信系統(tǒng),。

參考文獻(xiàn)

　?。?］ 劉嘉興，何世彪.混沌測(cè)控的概念,、特性與實(shí)現(xiàn)［J］.飛行器測(cè)控學(xué)報(bào),，2011，30(1):1-5.

　?。?］ 俞斌,，賈雅瓊.一種新的混沌擴(kuò)頻序列及其性能分析［J］.電子技術(shù)應(yīng)用，2014,39（1）：136-137.

　?。?］ 杜秀麗,，甄旭亮，陳波.基于混沌復(fù)合序列的直擴(kuò)系統(tǒng)及其性能分析［J］.計(jì)算機(jī)仿真,2013,30(11):173-176.

　?。?］ 黃展,，陳曉萍，趙衛(wèi)東.截短混沌擴(kuò)頻序列的優(yōu)選與性能分析［J］.電訊技術(shù),，2011,51(2):11-15.

　?。?］ VOLOS C, KYPRIANIDIS I M, STOUBOLOS I N. Motion control of robots using a chaotic truly random bits generator［J］.Journal of Engineering Science and Technology Review,2012,5(2):6-11.

　　［6］ 張曉蓉,，吳成茂.基于混沌與自編碼相關(guān)融合擴(kuò)頻碼的構(gòu)造［J］.電訊技術(shù),，2014,54(6):769-773.

　　［7］ 廉晨，達(dá)新宇,，張亞普.一種新型混沌擴(kuò)頻衛(wèi)星隱蔽通信算法［J］.計(jì)算機(jī)科學(xué),，2014,41（11）：158-161.

　　［8］ 易新兵,，楊凱.復(fù)合混沌碼的直擴(kuò)系統(tǒng)優(yōu)化及抗干性能研究［J］.計(jì)算機(jī)工程與設(shè)計(jì),2012,33(10):3716-3719.

　?。?］ 余振標(biāo)，馮久超.一種混沌擴(kuò)頻序列的產(chǎn)生方法及其優(yōu)選算法［J］.物理學(xué)報(bào),，2008,57(03):1409-1415.

　?。?0］ Yu Jin, Yao Yudong. Detection performance of chaotic spreading LPI waveforms［J］. IEEE Transaction on Wireless Communications,2005,4(2):390-396.