0 引言

    數(shù)控振蕩器(Numerically Controlled Oscillator,，NCO)是信號處理系統(tǒng)的重要組成部分,。隨著現(xiàn)代通信系統(tǒng)的不斷發(fā)展，NCO憑借其相位可連續(xù)線性變化,、頻率分辨率高,、全數(shù)字化處理等優(yōu)越特性，在圖像處理,、快速傅里葉變換,、直接數(shù)字頻率合成器等設(shè)計中得到了廣泛應(yīng)用。

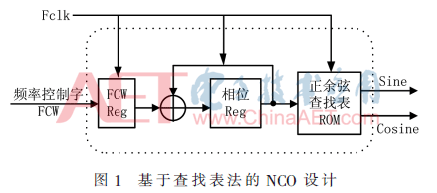
    傳統(tǒng)數(shù)控振蕩器的實現(xiàn)方法為只讀存儲器查找表法（ROM LUT）,，如圖1所示,。這種方法在對分辨率要求不高的情況下,，是一種簡單的實現(xiàn)方式。但是若要進一步提高分辨率,，就會消耗大量的ROM資源,；此外，存儲器讀取速度的瓶頸也限制了NCO的輸出速度,。而CORDIC算法易于使用數(shù)字電路實現(xiàn)，僅通過簡單的加減法和移位操作就可以完成多種硬件電路難以直接實現(xiàn)的復(fù)雜運算,，因此在NCO的設(shè)計中也得到了很好的應(yīng)用,。本文將對傳統(tǒng)CORDIC算法進一步改進，并結(jié)合改進方法提出一種適合于硬件實現(xiàn)的數(shù)控振蕩器的設(shè)計方法,，從而提高輸出精度和運算速度,。

1 CORDIC算法原理

    坐標(biāo)旋轉(zhuǎn)數(shù)字計算(Coordinate Rotation Digital Computer，CORDIC)首次由Jack Volder于1959年提出,，1971年Walther統(tǒng)一了CORDIC算法的形式,。CORDIC的基本思想是通過一系列只與運算基數(shù)有關(guān)的固定小角度的不斷偏擺從而逼近期望角度，此算法具有線性收斂域和序列特性^[3],。

    CORDIC算法的基本原理是運用了Givens旋轉(zhuǎn)法則,。假設(shè)給定向量A(x₀，y₀),，當(dāng)旋轉(zhuǎn)過一定角度θ后得到新向量B(x₁,，y₁)，如圖2所示,。

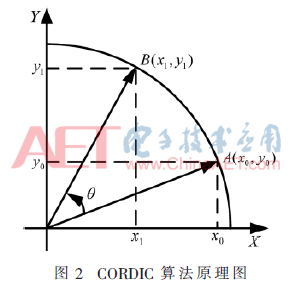
    根據(jù)旋轉(zhuǎn)變換法則,，可得式(1)：

    當(dāng)N→∞時，K_N收斂于一個常數(shù),，即K_N≈0.607 252 935,。當(dāng)?shù)螖?shù)N得到確定，K_N的值也就確定了,，可以把它看作一個常數(shù),，所以只要提前計算出定標(biāo)因子K_N，就能正確地使用式(6)進行CORDIC求值運算,?？梢妼τ诿恳淮涡〗嵌圈?sub>i的旋轉(zhuǎn)運算，實際上只與δ_i2^-i運算有關(guān),，這在硬件上的反映就是加/減法和移位操作,。

    最后，通過引入?yún)?shù)z表示當(dāng)前角度和期望角度的偏差值,，來確定下一次旋轉(zhuǎn)的方向,，即判斷δ的符號,。令z_i+1=z_i-θ_i(z₀=θ，i=0,，1,，…，N-1),，當(dāng)z≥0時,，δ=+1；當(dāng)z≤0時,，δ=-1,。若經(jīng)過多次旋轉(zhuǎn)后，就可以得到與期望角度充分接近的旋轉(zhuǎn)向量,。如果選取初始值(x₀,，y₀)=(K_N，0),，在進行N次迭代運算后,，結(jié)果將收斂于(sinθ，cosθ),。

2 CORDIC算法改進

2.1 算法迭代結(jié)構(gòu)

    由CORDIC算法的原理可以看出,，此算法每一次的運算結(jié)構(gòu)相似，具有可迭代的特性,。對于傳統(tǒng)的反饋結(jié)構(gòu),，每次運算都利用同一組硬件反復(fù)進行迭代，此結(jié)構(gòu)占用硬件資源少,，能夠在一定程度上縮小電路面積,。但是由于需要不斷向輸入端反饋輸出數(shù)據(jù)，而且還需要一個狀態(tài)機來跟蹤全部迭代過程,，會導(dǎo)致整個系統(tǒng)運行速度降低,，吞吐量減小。如果需要實現(xiàn)高速高精度的輸出,，就必須采用高速全流水線結(jié)構(gòu),，如圖3所示。流水線結(jié)構(gòu)的每一級迭代都使用單獨的運算單元,，與反饋結(jié)構(gòu)相比,，雖然消耗了較多的硬件資源，但換來的是運算速度提高,，吞吐量增大,，特別適合在硬件上實現(xiàn)^[4]。

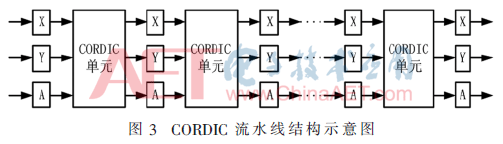
    此外,，有限次數(shù)的迭代運算通常無法完全消除累加角度與期望角度間的誤差,，因此我們引入殘余角誤差ε,，并將式(4)改寫為：

    由式(8)可以看出，隨著迭代次數(shù)或者流水級數(shù)的不斷增加,，近似誤差ε的趨勢是減小的,，角度累加所得到的值會逐漸逼近期望角度，CORDIC算法的精度也會不斷提高,。但是考慮到實際設(shè)計中不能無限制增加流水線級數(shù),，一方面流水線級數(shù)過多會降低系統(tǒng)整體運算速度，另一方面流水增加至一定級數(shù)后,，對精度的提高微乎其微,，但是卻消耗了大量的硬件資源，因此必須選擇適合的流水線級數(shù),，來控制硬件成本和計算復(fù)雜度。根據(jù)Yu Hen Hu提出ε的上界^[8]：

其中A_N-1為最后一次的旋轉(zhuǎn)角度,，N為旋轉(zhuǎn)次數(shù),。為了達到所需要的精度，我們選擇N=16,，即通過16級并行流水線結(jié)構(gòu)來實現(xiàn)CORDIC算法,。

2.2 覆蓋角度擴展

    CORDIC算法每一級的角度旋轉(zhuǎn)由式(3)得到了確定，表1中列舉了其中的部分角度,。

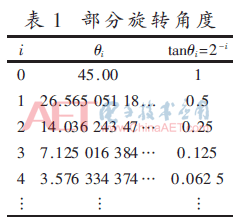
    式(3)是關(guān)于i的遞減函數(shù),，將這些角度累加，當(dāng)i→∞時：

    可見CORDIC算法能夠計算角度的收斂域為[-99.88°,，99.88°],，而我們需要輸出整個圓周范圍內(nèi)角度的正余弦值，顯然常規(guī)的方法無法滿足,。

    利用三角函數(shù)的對稱性,，通過象限轉(zhuǎn)移的方法就能夠?qū)⒂嬎憬嵌葦U展至[-π，π],。文獻[5]將[-π,，π]映射至[0，π/4],，但是在最后對輸出的一組數(shù)據(jù)是否交換或改變符號需要進行判斷,，而文獻[7]中將[-π，π]映射至[0,，π/8],，但需要對產(chǎn)生的常數(shù)因子進行補償。本文將整個圓周[-π,，π]劃分為8個象限(如圖4所示),，并將所有角度映射至[-π/4,，π/4]，即1號和8號象限,，并同時對初始值X₀和Y₀進行處理,。這樣既不會產(chǎn)生額外的常數(shù)因子，也不需要在最后對輸出結(jié)果進行數(shù)據(jù)交換或符號改變,。

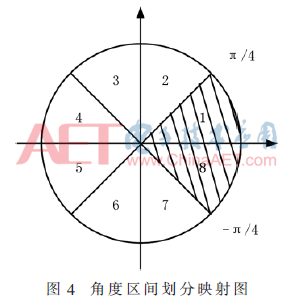
    利用三角函數(shù)的對稱性,，根據(jù)θ所在象限，對初始值分別做如表2的處理,。

    這樣的數(shù)據(jù)預(yù)處理過程雖然會消耗一定的硬件資源,，但特別適合流水線結(jié)構(gòu)的CORDIC算法，對提高整個系統(tǒng)的速度有很大幫助,。

2.3 計算數(shù)據(jù)位擴展

    在實際電路的實現(xiàn)中,，由于CORDIC算法每一級迭代使用的都是有限精度的代數(shù)計算，就導(dǎo)致了另外一種誤差,，這種因數(shù)據(jù)位寬有限而產(chǎn)生的誤差稱為舍入誤差,。所以除了增加迭代次數(shù)以外，還可以通過擴展CORDIC算法數(shù)據(jù)的位寬來提高精度,。舍入誤差σ的大小與運算數(shù)據(jù)的位寬b有關(guān),，根據(jù)σ=2^-b-1這一關(guān)系式可知，操作數(shù)的位寬每擴展一位,，就能夠?qū)⑸崛胝`差縮小為原來的一半,。當(dāng)增加流水的級數(shù)無法大幅提高算法精度時，擴展CORDIC計算數(shù)據(jù)位寬是另一種很好的方法,，如圖5所示,。

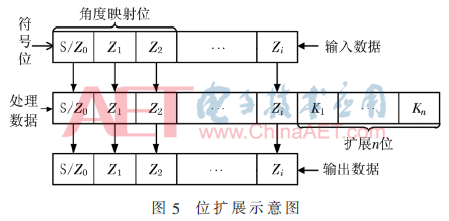
    在本設(shè)計中，由于NCO后端接入了混頻模塊,，輸出數(shù)據(jù)必須為16位與之匹配,，但是在CORDIC內(nèi)部迭代計算時，我們把數(shù)據(jù)擴展至20位,，最后對輸出結(jié)果截位處理,，然后再送入下一級。通過對數(shù)據(jù)位寬擴展4位的方法,，可以有效地提高運算精度,。

3 基于CORDIC改進算法的NCO系統(tǒng)結(jié)構(gòu)

    NCO主要用于產(chǎn)生正、余弦信號,，本設(shè)計基于CORDIC改進算法,，由前端處理、CORDIC迭代以及輸出處理這3個部分組成，其系統(tǒng)結(jié)構(gòu)如圖6,。當(dāng)輸入不同的頻率控制字時,，NCO輸出波形的頻率也隨之改變。

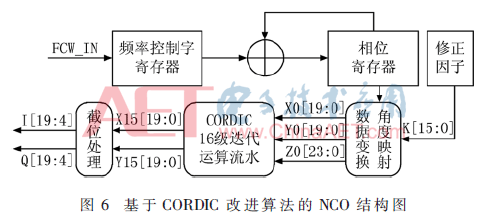
    在前端處理中,，我們采用了24位相位累加器以保證頻率分辨率達到要求,，并通過判斷相位值的高3位θ[23：21]，將目標(biāo)角度映射至[-π/4,π/4]區(qū)間,，具體映射方法見表2,；而修正因子可以根據(jù)式(7)求出，由于算法的流水級數(shù)事先已經(jīng)確定,，所以只要將N=16代入就可以準(zhǔn)確的得到K_N,，再通過數(shù)據(jù)預(yù)處理確定X₀和Y₀的初始值，從而在迭代之前就完成對輸出結(jié)果的補償,，進一步提高整個系統(tǒng)的速度,。

    第二部分為16級CORDIC流水線，它是整個系統(tǒng)的核心,，流水線結(jié)構(gòu)中的每一行相當(dāng)于CORDIC算法中的一級迭代,，其硬件結(jié)構(gòu)如圖7所示。每一級電路包括三個加/減法器和兩個移位器,，其中A_i表示各級基本旋轉(zhuǎn)角度值，Sign為各級運算的加/減控制信號,，它的符號由Z_i的最高位確定,。

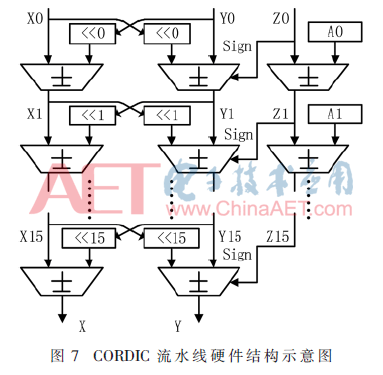
    最后一部分對數(shù)據(jù)舍入截位，并輸出正,、余弦兩路信號,。本設(shè)計適用于多種旋轉(zhuǎn)精度的需求，靈活性好,，資源利用率高,，全并行流水的結(jié)構(gòu)具有速度快、吞吐量大的特點,。

4 系統(tǒng)仿真及性能分析

    本設(shè)計根據(jù)圖5,，在Xilinx ISE 14.7環(huán)境下搭建軟件平臺，采用Verilog HDL硬件描述語言完成編譯綜合,，使用Modelsim SE 10.1c進行功能仿真驗證,，最后通過MATLAB R2012b對結(jié)果進行分析。

    在Xilinx ISE中完成代碼編寫后,，調(diào)用Modelsim進行軟件仿真,，當(dāng)輸入不同頻率控制字，得到NCO產(chǎn)生的正余弦信號結(jié)果如圖8所示。從圖中可以看出,，生成的 I,、Q兩路波形信號具有完全正交性，并且經(jīng)過角度映射后實現(xiàn)了整個圓周區(qū)間的覆蓋,，完全可以替代基于查找表的傳統(tǒng)NCO設(shè)計方式,。

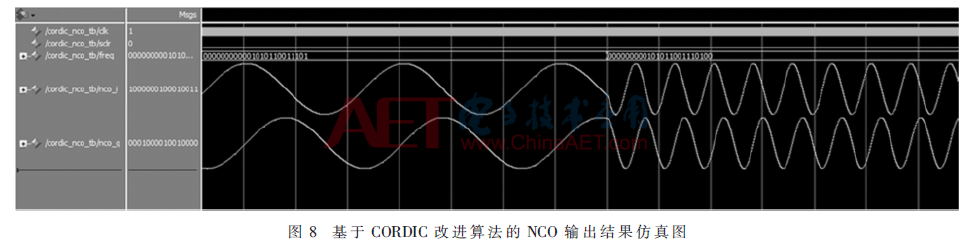
    本文選用Xilinx Virtex-4芯片，經(jīng)過Xilinx ISE對代碼編譯綜合后,，得到設(shè)計所消耗的硬件資源及最高工作頻率等信息,。在16位小數(shù)精度、16級流水迭代的情況下,，傳統(tǒng)CORDIC算法設(shè)計而成的NCO使用了1 021個邏輯單元,，而基于CORDIC改進算法的NCO模塊使用了904個邏輯單元，節(jié)省了約11.46%的硬件資源,。從表3可以看出,，采用經(jīng)過優(yōu)化后的CORDIC算法，系統(tǒng)最高頻率可達287.64 MHz,，比基于查表法及常規(guī)CORDIC算法NCO的性能分別提高了354.6%和144.3%,。

    最后將Modelsim仿真得出的數(shù)據(jù)在[-π，π]之間平均采樣5 000個點并導(dǎo)入MATLAB,，經(jīng)過處理后得到圖9,。再從[-π/4，π/4]中選取若干角度進行誤差對比分析,，如表4所示,。

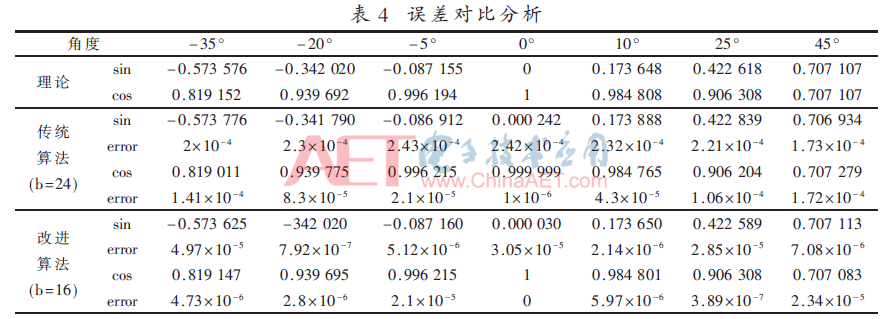
    I、Q通路正余弦值的誤差主要由迭代次數(shù)以及位寬的限制引起,，通過對表4的數(shù)據(jù)分析可知,，傳統(tǒng)算法在使用24位小數(shù)位的情況下進行運算，誤差達到10^-4,；而基于本文的CORDIC改進算法僅使用16位數(shù)據(jù)位寬就能夠?qū)⒕忍嵘?0^-5~10^-6的數(shù)量級,，所以本設(shè)計在提高精度的同時還減少了硬件資源的消耗，在精度和面積上均具有一定的優(yōu)勢,。

5 結(jié)束語

    本文在傳統(tǒng)CORDIC算法基礎(chǔ)上,，提出改進方案并應(yīng)用于數(shù)字控制振蕩器的設(shè)計，通過仿真驗證及性能分析證明其可行性,。實驗結(jié)果表明,，本設(shè)計進一步提升了系統(tǒng)的速度和精度，并在一定程度上減少了硬件資源消耗,。目前,，該NCO模塊已經(jīng)成功的應(yīng)用于某DDC芯片的產(chǎn)品中，并且表現(xiàn)出良好的性能及穩(wěn)定性。

參考文獻

[1] LIU Y,，F(xiàn)AN L,，MA T.A modified CORDIC FPGA implementation for wave generation[J].Circuits，Systems and Signal Processing,，2014,，33(1)：321-329.

[2] Pramod Kumar Meher，Sang Yoon Park.CORDIC designs for fixed angle[J].IEEE Transaction on Very Large Scale Integration(VLSI) System,，2013,，21(2)：217-227.

[3] 張曉彤，辛茹.基于改進混合式CORDIC算法的直接數(shù)字頻率合成器設(shè)計[J].電子學(xué)報,，2008,，36(6)：1144-1148.

[4] KAUSHIK B，RAKESH B.Architectural design and FPGA implementation of radix-4 CORDIC proseccor[J].Micropro-cessors and Microsystems,，2010,，34(2-4)：96-101.

[5] 徐成，秦云川.免縮放因子雙步旋轉(zhuǎn)CORDIC算法[J].電子學(xué)報,，2014,，42（7）：1441-1445.

[6] 張朝柱，韓吉南,，燕慧智.高速高精度固定角度旋轉(zhuǎn)CORDIC算法的設(shè)計與實現(xiàn)[J].電子學(xué)報,，2016，44（2）：485-490.

[7] MAHARATNA K,，BANERJEE S,，GRASS E，et al.Modified virtually scaling-free adaptive CORDIC rotator algorithm and architecture[J].IEEE Transaction on Circits Systems for Video Technolog,，2005，15(11)：1463-1474.

[8] HU H Y.The quantization effects of the CORDIC algorithm[J].IEEE Transactions on Signal Processing,，1992,，40：834-844.

作者信息:

王申卓，胡春林,，胡廣垠,，徐大誠

（蘇州大學(xué) 電子信息學(xué)院，江蘇 蘇州215000）