邱菁，黃繼偉,，陳阿輝,，柯玉山

　　（福州大學(xué) 物理與信息工程學(xué)院,，福建 福州350002）

　　摘要：在調(diào)頻連續(xù)波（FMCW）雷達測距算法中,，快速傅里葉（FFT）算法頻譜分析的誤差是由FFT頻譜線之間間隔造成的。因此,，為了提高FFT算法的測距精度,，減少頻譜分析的誤差，提出了頻移補償?shù)母倪M措施,。頻移補償?shù)念l譜搬移因子的獲取是利用頻譜圖對稱性與最值和鄰近兩個譜線點坐標(biāo)之間的距離差得到的,。仿真實驗的結(jié)果說明，該措施在不大幅提高測距時間的情況下得到的最值更接近實際峰值,，可以較好地改進雷達的測距精度,。

　　關(guān)鍵詞：傅里葉變換；雷達,；譜最大值估計算法,；測距精度；頻譜偏移

　　中圖分類號：TN953+.2文獻標(biāo)識碼：ADOI： 10.19358/j.issn.1674-7720.2017.09.007

　　引用格式：邱菁,，黃繼偉,，陳阿輝，等.高精度調(diào)頻連續(xù)波雷達測距算法的研究［J］.微型機與應(yīng)用,，2017,36（9）：22-24,，27.

0引言

　　*基金項目： 福建省科技計劃項目（2014H0026）

　　常用的雷達測距有調(diào)頻連續(xù)波和單脈沖雷達，其中調(diào)頻連續(xù)波雷達具有較高的距離分辨率,、低功率以及無測量盲區(qū)等特點［1 4］,。調(diào)頻連續(xù)波雷達廣泛應(yīng)用于雷達測距系統(tǒng)中，通過對信號進行采樣和FFT算法分析進而提取測量距離的信息,。由于FFT本身的“柵欄效應(yīng)”,，存在著較大的誤差。而工業(yè)上如油罐的液位測量等應(yīng)用中［5 6］,，對測量的精度有很高的要求,。人們常用提高頻率細化率來提高精度，卻增加了計算時間,。因而產(chǎn)生了擬合法［7］,、Rife算法［8］,、譜最大值估計算法［8 11］、CZT［10 15］等方法來提高測距精度,。其中CZT算法精度最高。本文對這些方法進行改進,，設(shè)計了一個利用坐標(biāo)中最值和鄰近兩個譜線點坐標(biāo)之間距離差的方法與CZT相結(jié)合來改進測距精度,，并對此進行了仿真和驗證。

1FMCW雷達測距原理分析和誤差分析

　　文獻［10 18］對雷達測量原理進行了分析,。雷達測距原理是混頻器通過雷達測距系統(tǒng)的天線獲得發(fā)射和接收信號,，從而得到差頻信號［16 18］，通過差頻信號的主頻來提取距離信息,，然后對距離信息進行數(shù)字信號處理獲得目標(biāo)距離,。圖1是發(fā)射信號與回波信號的時域關(guān)系。

　　圖1中實線為雷達信號發(fā)射器發(fā)出的發(fā)射信號頻率與時間的關(guān)系,，虛線則為接收到的回波信號,。雷達發(fā)射信號的本振信號與接收信號經(jīng)過混頻器混頻之后可以得到差頻信號。要獲得所測量的距離就需要利用差頻信號進行傅里葉變換,，獲取頻譜圖的最大采樣值,。

　　傅里葉變換就是把連續(xù)的時間利用加窗函數(shù)進行截斷，截斷成N點滿足DFT在時域和頻域上的離散信號的要求,。而這些離散點之間存在著間隔,，會受到柵欄效應(yīng)的影響，所以FFT處理后采樣點之間的間隔△R使得信號處理后的峰值會相對理論峰值偏左或者偏右,。所以通過最大采樣點的頻率值計算出來的距離會產(chǎn)生△R/2的測距誤差,。其中這N個離散的譜線包絡(luò)可以近似為一條曲線，但與理論的曲線相比,，并不是對稱的,。為了減少誤差，可以通過增加N點的大小,，當(dāng)大量增加N點的值時,，采樣點間隔會越來越密，包絡(luò)的峰值也會不斷增大,，兩側(cè)的值也就越來越接近,，逐步形成一個類似拋物線的對稱曲線，而測得的距離誤差也隨之降低,。但是運算量會大大增加,，處理的速度也會變慢，對雷達系統(tǒng)的實時性造成不少影響［812］,。

2利用頻譜圖坐標(biāo)估計最大采樣點

　　對于譜最大值估計算法,，文獻［910］提到當(dāng)理論的采樣點與實際的采樣點一致時,，次大值就為0。但該方法也無法保證理論與實際的采樣點的最大值是一樣的,，所以次大值不為零,。由于FFT頻譜圖是對稱的，也就可以近似認為頻譜圖中最大采樣值點到相鄰的兩點的距離是相等的,。由于FFT存在的柵欄效應(yīng)兩邊的距離不一致,，即存在最大值兩邊的次大值不一樣。根據(jù)排序分為3個大小不一樣的幅度值,，以最大值為圓心,，最大值與次大值的距離為半徑畫圓可以交于最大值與第三大值兩點所在的直線上，兩者之間會有距離差,，而當(dāng)兩者之間的距離差小于某個值時,，可以認為此時最大值點就是所要找的最大采樣點，如圖2所示,。

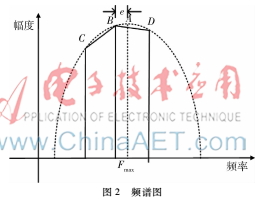
　　取頻譜圖上最大值及相鄰兩邊的值B(f1,k1),、C(f3,k3)、D(f2,k2),，其中B對應(yīng)的譜線是頻譜線上的最大值,D是譜線的次大值,，C是第三大值。則頻譜的最大值A(chǔ)在B~D之間,，由于距離譜是關(guān)于最大值對稱的,因此可以認為當(dāng)B與A重合時,，D的對稱點為C。

　　首先設(shè)定誤差為Δf1,，然后通過對最大值點到兩個相鄰序列的距離差Δk的分析,，取BC、BD在坐標(biāo)軸上線段距離的差值即距離差的一半作為估值點帶入距離公式獲得相應(yīng)的值Δf,，再通過比較BD,、BC距離的大小來判斷B點相對于最大值偏左還是偏右，把頻譜左右移動Δf就可以獲得B的新坐標(biāo)值,，可以得到新的距離差Δk以及Δf,，對比Δf，若Δf1<Δf,，需要重新對頻譜進行移動,，重復(fù)上面的方法，直到細分的Δf小于誤差為止,。該方法就是通過縮小距離差來獲得最大值點,。設(shè)D、B,、C分別是頻譜的次大值,、峰值和第三大值,，A為實際的頻譜峰值，則線段BC與線段BD相等,，B在D的左側(cè),。若B與主瓣實際的峰值一樣，根據(jù)距離相等可得：

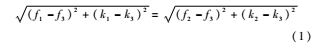
　　若B與主瓣的實際峰值不一樣,，可以設(shè)兩者的距離差為Δk,，有：

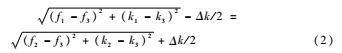
　　設(shè)B點與主瓣峰值中心點的差值為Δf。設(shè)主瓣的中心點坐標(biāo)為(f1+Δf,k1+Δk1),，由式（1）可得：

　　其中對于頻譜上最大的3個點是序列號相鄰的3個值，則可得f1,、f2相差2個序列且f1+f2=2×f3,。當(dāng)整個頻譜左右移動時，B,、C,、D所在的點的幅值也會相應(yīng)增加或減少，設(shè)Δk1,、Δk/2近似相等,，則把式（2）結(jié)果帶入到式（5）即可解出Δf。

　　然后整個頻譜平移Δf,，至于平移的方向需要依靠最大值和次大值的序列號的大小來決定,。若次大值f2<f3，則整個頻譜左移d,；若f2>f3,則整個頻譜右移,。

　　再次獲得此時的B、C,、D 3個點的新坐標(biāo),，設(shè)誤差為Δf1，當(dāng)BC,、BD的距離誤差大于這個值則重復(fù)上面的步驟,；當(dāng)BC、BD的距離誤差小于這個值,，結(jié)束運行,。所得到的B點就是峰值點。圖3為改進后的算法流程圖,。

3仿真與驗證

　　對上述所述的方法進行仿真和驗證,，并對比不同距離下不同方法的仿真程序運行的精度。雷達發(fā)射波的仿真條件為：

　　調(diào)頻信號的帶寬B為109 Hz,；

　　鋸齒波調(diào)制信號的周期T為0.2 s,；

　　中心頻率為24×109 Hz,。

　　對雷達的發(fā)射信號、回波信號,、差頻信號進行仿真,，如圖4、圖5所示,。

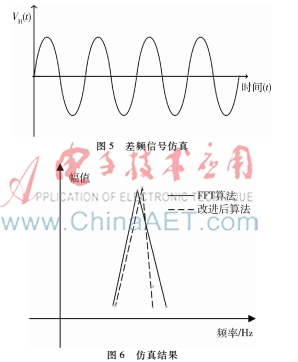
　　設(shè)定目標(biāo)的位置為100 m,，得到如圖6所示的頻譜。根據(jù)FFT法,，取N=1 024,，目標(biāo)所在的位置為99.61 m，誤差為0.39%,，然而經(jīng)過最大值法得到目標(biāo)所在的位置為99.98 m,，誤差為0.02%。

　　設(shè)定距離范圍為10～100 m,，目標(biāo)為單目標(biāo)時的計算機仿真結(jié)果見表1,。

4結(jié)束語

　　本文對雷達系統(tǒng)測距過程和原理進行分析，對測距算法進行一定改進,，利用坐標(biāo)的距離差提出了一種簡單估計目標(biāo)真實位置的方法,，并將該方法與傳統(tǒng)的快速傅里葉變換進行了對比。仿真實驗結(jié)果說明該方法可以較好地改進雷達的測距精度,。經(jīng)過對時間的測量,，F(xiàn)FT算法用時0.02 s，改進后用時0.034 s,，頻譜平移的次數(shù)在10次以內(nèi),，對時間的影響不大。

　　參考文獻

　?。?］ 包敏.線性調(diào)頻連續(xù)波雷達信號處理技術(shù)研究與硬件實現(xiàn)［D］. 西安：西安電子科技大學(xué),，2009.

　　［2］ 郭云,，余奎,，陳堅.幾種連續(xù)波雷達系統(tǒng)參數(shù)設(shè)計和信號處理方法［J］.電子科技,2015，28(2):158-163.

　?。?］ 孫艷敏,，周長林，常青美,等.減少防撞雷達虛假目標(biāo)的信號處理研究［J］. 微型機與應(yīng)用,，2011,，30(18):46-51.

　　［4］ 胡玉蘭,，趙子銘,，片兆宇.高分辨雷達一維距離像的融合特征識別［J］. 微型機與應(yīng)用,，2015，34(4):52-57.

　?。?］ ZHU L, DONG L, LIU S D, et al. Selfadaptive frequency estimation algorithm of improving liquid level measurement precision of LFMCW radar［C］. 2010 International Conference on Microwave and Millimeter Wave Technology(ICMMT), IEEE, 2010:16261628.

　?。?］ 王保華．近程LFMCW 雷達測距系統(tǒng)的研究與實現(xiàn)［D］. 重慶：重慶大學(xué)，2012．

　?。?］ 周清晨,，徐海洲，常城,，等.基于拋物線擬合方法的提高雷達測距精度研究［J］.信息通信,，2016(6):8-9.

　　［8］ 于衛(wèi)東,，涂亞慶,，詹啟東，等,，基于改進Rife算法的LFMCW雷達測距方法及實現(xiàn)［J］.電子測量與儀器學(xué)報，2015,，29(4)：550-557.

　?。?］ 徐軍榮，于盛林.提高FMCW雷達測距精度的譜最大值估值算法［J］.計算機技術(shù)與發(fā)展,，2009,，19(4):73-79.

　　［10］ 王琨.調(diào)頻連續(xù)波雷達在雷達測距中的算法研究［D］. 天津：河北工業(yè)大學(xué),，2013.

　?。?1］ 韓輝，冷建偉,，安飛.FMCW雷達物位系統(tǒng)的算法設(shè)計［J］. 天津理工大學(xué)學(xué)報,，2011，27(4)：27-31.

　?。?2］ 朱愷,，秦軼煒，許建中,，等．四種提高FMCW測距精度的方案及性能分析［J］．無線電工程,，2015，45(1):20-25.

　?。?3］ 譚曉衡,，周帥，黃振林．基于小波包的24 GHz LFMCW雷達測距方法［J］．系統(tǒng)工程與電子技術(shù),，2013,，35(3):522-526.

　?。?4］ 陳璟.數(shù)字信號處理中加窗插值FFT算法的研究［J］.黑龍江科學(xué)，2013,，4(4):40-42.