0 引言

    海雜波環(huán)境下的小目標(biāo)檢測在航行安全,、災(zāi)害搜救、海岸管理和國土安全等方面具有重要實際意義,，利用電磁波對海上目標(biāo)進(jìn)行實時,、可靠和自動化搜索也成為當(dāng)前的研究熱點。

    但海洋小目標(biāo)檢測面臨嚴(yán)峻挑戰(zhàn)：海雜波建模困難,；小目標(biāo)信雜比較低,，速度較慢，多普勒域易被海雜波掩蓋^[1],。近年來,，國內(nèi)外學(xué)者圍繞該課題展開的研究主要分為下面幾類。(1)基于統(tǒng)計模型的恒虛警(Constant False Alarm Rate,，CFAR)檢測方法^[2]：對海雜波建立不同的統(tǒng)計模型,，通過實時估計雜波背景產(chǎn)生自適應(yīng)門限進(jìn)行檢測處理；隨著雷達(dá)分辨率的提高,，非高斯模型下的恒虛警檢測器由此誕生,。(2)基于混沌^[3]、分形^[4]和神經(jīng)網(wǎng)絡(luò)^[5]的檢測方法：HAKYIN S教授率先發(fā)現(xiàn)了海雜波的混沌特性^[3],，但對雜波的混沌模型目前尚存爭議,；HU J 等人證明了海雜波的分形行為^[4]，但分形目標(biāo)檢測算法對相位信息未有效利用,；LEUNG H等人利用神經(jīng)網(wǎng)絡(luò)的非線性逼近特性,，通過預(yù)測誤差實現(xiàn)目標(biāo)檢測^[5]，但需很高的訓(xùn)練精度,。(3)自適應(yīng)匹配算法^[6]：基于海雜波球不變隨機向量(Spherical Invariant Random Vector,，SIRV)模型，通過估計雜波協(xié)方差矩陣實現(xiàn)目標(biāo)檢測,，但需解決信噪比損失和積累樣本數(shù)間的矛盾,。(4)基于時頻分析的目標(biāo)檢測方法^[7]：描述了信號在時頻域的變化情況,，如短時傅里葉變換和小波變換等，但其分析能力會受到基函數(shù)的影響,。

    本文借助岸基微波雷達(dá)平臺和相應(yīng)的實測數(shù)據(jù)展開研究,，并基于經(jīng)驗?zāi)Ｊ椒纸猓‥mpirical Mode Decomposition，EMD）實現(xiàn)目標(biāo)檢測,。EMD 算法對信號的分析是基于時域信號本身,，不需要基函數(shù),，但其在目標(biāo)檢測中的運用需實現(xiàn)模態(tài)分量的自動篩選和判別^[8],。文中算法結(jié)合特征譜分析實現(xiàn)基于EMD的自適應(yīng)目標(biāo)檢測。

1 基于模態(tài)函數(shù)特征譜的目標(biāo)檢測算法

1.1 EMD算法

    EMD算法能夠根據(jù)信號的局部極值點自適應(yīng)地對信號進(jìn)行分解,，分解出來的內(nèi)模函數(shù)(Intrinsic Mode Function,，IMF)分量可代表一種簡單振蕩，所在頻帶隨著分解層次的增加逐漸降低,。對于信號x(t),，可由EMD算法分解得到n個內(nèi)模函數(shù)分量hi(t)和一個剩余分量r_n(t)^[8]：

1.2 模態(tài)函數(shù)特征譜

    由EMD算法分解出的模態(tài)函數(shù)頻率逐漸降低，含目標(biāo)的IMF分量可由人為篩選而檢測出來,，但如何自動篩選和判別是實現(xiàn)算法自適應(yīng)性的關(guān)鍵,。包含目標(biāo)IMF與純海雜波的多普勒譜差異是含有尖峰單頻信號，可對其進(jìn)行諧波分析^[9],。在駐留時間較短的條件下,，雷達(dá)回波可近似認(rèn)為是由有限單頻信號疊加而成： 

其中，L為回波信號中包含的諧波次數(shù),，w(n)是均值為0,、方差為σ²的復(fù)高斯白噪聲，φ_i為初始相位,。樣本長度為K,，則回波自相關(guān)陣為：

1.3 算法流程

    基于模態(tài)函數(shù)特征譜的海洋小目標(biāo)檢測算法流程如圖1所示。首先,，對雷達(dá)回波利用復(fù)數(shù)EMD進(jìn)行分解,；然后對得到的各個內(nèi)模分量提取相關(guān)矩陣，特征值分解得到特征譜,，并根據(jù)特征譜分布情況得到散布特征,；最后基于散布特征在各個內(nèi)模函數(shù)間的分布差異實現(xiàn)自適應(yīng)目標(biāo)檢測。

2 實測數(shù)據(jù)處理

2.1 實測數(shù)據(jù)來源

    實測數(shù)據(jù)來自武漢大學(xué)無線電海洋遙感實驗室自主研制的微波多普勒雷達(dá)(Microwave Ocean Remote SEnsor,，MORSE)^[10],。2012年底，MORSE雷達(dá)在中國南海的遮浪島進(jìn)行一個多月的海邊試驗,，工作頻率設(shè)為2.85 GHz,，采用調(diào)頻中斷連續(xù)波,，探測范圍200 m~2 km，距離分辨率7.5 m,。選取含慢速弱小目標(biāo)的4組數(shù)據(jù)#1~#4,，其包含80個距離元，持續(xù)時間171 s,，環(huán)境參數(shù)和目標(biāo)信息如表1所示,，能量分布如圖2所示。其中,，海浪參量來自浮標(biāo)數(shù)據(jù),，目標(biāo)是附近來往的慢速小船只，能量較弱,。

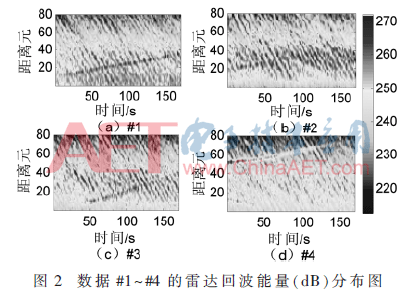
2.2 實測數(shù)據(jù)處理過程和檢測結(jié)果

2.2.1 基于EMD的傳統(tǒng)目標(biāo)檢測算法

    從數(shù)據(jù)組#1中選取包含移動目標(biāo)的一段數(shù)據(jù),，其來自第15距離元中第30 s~31 s時間段，包含256個點,。對數(shù)據(jù)進(jìn)行EMD分解,，如圖3所示，左側(cè)是前3個正負(fù)IMF的時域波形,，右邊是相應(yīng)多普勒頻譜,。從IMF分量的波形圖可以看出，EMD分解所得的正,、負(fù)IMF分量的頻率依次降低,。而且目標(biāo)存在于x_-1中，可用x_-1重構(gòu)目標(biāo)回波信號,，實現(xiàn)海雜波抑制和目標(biāo)檢測,。

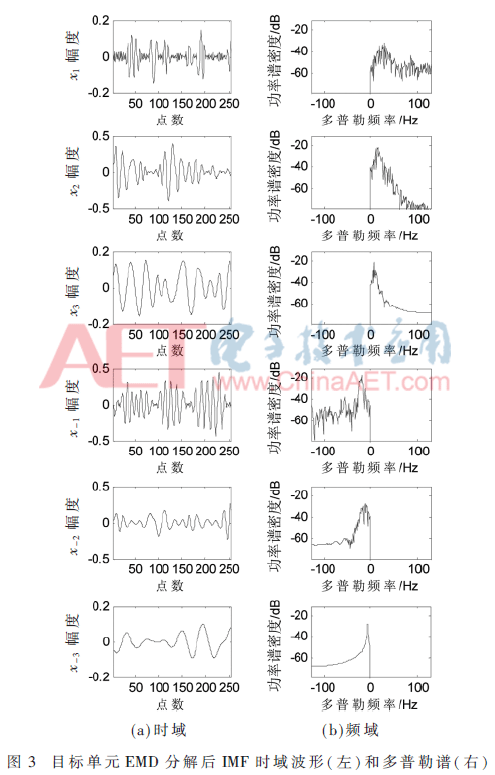
    按照復(fù)數(shù) EMD中的信號重構(gòu)方法，得到如圖 4所示的原始信號和重構(gòu)信號的時頻域波形圖,。其中,，左圖是時域波形，右圖是其多普勒譜,。觀察發(fā)現(xiàn),，經(jīng)過 EMD 分解-分量篩選-信號重構(gòu)這一過程，頻率分量中的海雜波成分被剔除,，只留下目標(biāo)分量和基底噪聲,。

2.2.2 模態(tài)特征譜

    為實現(xiàn)含目標(biāo)模態(tài)函數(shù)的自適應(yīng)選擇，現(xiàn)在對EMD分解得到的模態(tài)函數(shù)分別進(jìn)行特征值分解得到其相應(yīng)的特征譜,，如圖5顯示了#1中海雜波和目標(biāo)單元前3個正負(fù)模態(tài)特征譜的分布情況,。

    由于目標(biāo)的多普勒頻移，x_-1的特征譜發(fā)生了明顯變化；海雜波能量主要分布在x₁之中,，故目標(biāo)和海雜波的特征譜差異主要體現(xiàn)在正負(fù)第一個模態(tài)分量上,。如圖5所示，相對海雜波而言,，含目標(biāo)的模態(tài)分量x_-1的諧波成分相對較少,，故在特征值分布中，大特征值的個數(shù)相對較少,。根據(jù)式(8)計算累積貢獻(xiàn)率達(dá)90%的大特征值個數(shù),，提取散布特征，其在內(nèi)模函數(shù)上的分布如圖6所示,。

    觀察發(fā)現(xiàn),，目標(biāo)的存在使得x_-1和x₁間的差異增大，而且在負(fù)頻模態(tài)函數(shù)中,，散布特征依次遞減的單調(diào)性被改變,。再結(jié)合目標(biāo)和海雜波單元的差異,，提取正負(fù)模態(tài)差值作為檢測量,，其在整場數(shù)據(jù)的分布情況如圖7所示。接著對其進(jìn)行自適應(yīng)門限檢測,，得到點跡分布圖,。

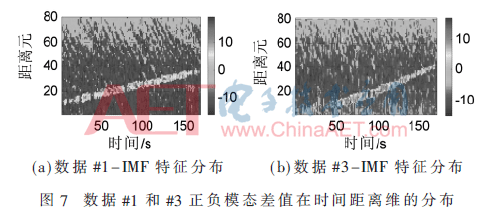
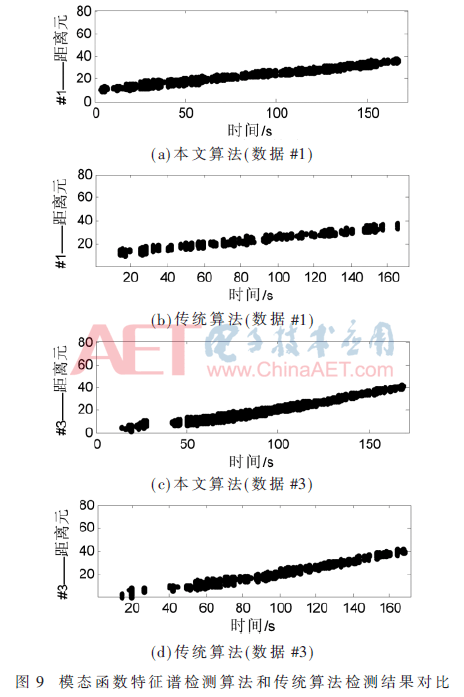
    為了與本文算法檢測結(jié)果形成對比，這里給出傳統(tǒng)恒虛警算法檢測結(jié)果,。傳統(tǒng)恒虛警檢測包括兩個關(guān)鍵因素：(1)檢測參量,；(2)CFAR檢測閾值?；贑FAR檢測器的基本結(jié)構(gòu),，提取不同檢測參量，就形成了不同的CFAR目標(biāo)檢測算法[7,，11],。若將峰值（方案1）和頻域峭度（Frequency-Domain Kurtosis, FDK）（方案2）分別作為檢測參量，就形成本文算法的對比方案,，如圖8所示,。本文算法和傳統(tǒng)算法中的方案1的檢測結(jié)果如圖9所示。觀察點跡分布可以發(fā)現(xiàn),，由于目標(biāo)慢速且弱小,，傳統(tǒng)算法檢測能力受限，本文算法的檢測概率相對較高,。

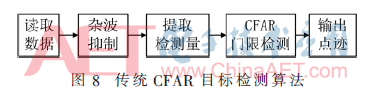
    對#1~#4進(jìn)行檢測處理,，虛警率為0.001時檢測概率如表2所示，對比發(fā)現(xiàn)，相對傳統(tǒng)CFAR檢測算法,，本文算法的檢測概率相對較高,。以上實測數(shù)據(jù)處理結(jié)果說明，基于模態(tài)函數(shù)特征譜的檢測算法可以實現(xiàn)海洋小目標(biāo)的有效檢測,。

3 結(jié)論

    經(jīng)驗?zāi)B(tài)分解算法用于分析非線性信號,，其分解過程是基于時域信號本身的局部特征，不需要基函數(shù),，其在海雜波抑制和目標(biāo)檢測方面具有應(yīng)用潛力,，但如何實現(xiàn)模態(tài)函數(shù)自動篩選和判別是算法的關(guān)鍵問題。而本文基于模態(tài)函數(shù)特征譜的檢測算法有效解決了此問題,，實現(xiàn)了基于EMD的目標(biāo)檢測算法的自適應(yīng)性,。在實測微波多普勒雷達(dá)數(shù)據(jù)中應(yīng)用該算法，并與傳統(tǒng)的恒虛警算法進(jìn)行對比,，結(jié)果表明：相對傳統(tǒng)算法,，文中算法不需要雜波抑制預(yù)處理環(huán)節(jié)，且在相同的虛警率約束下,，提高了目標(biāo)的檢測概率,。這為微波雷達(dá)海洋小目標(biāo)檢測提供了新的解決方法。

參考文獻(xiàn)

[1] 何友,，黃勇,，關(guān)鍵，等.海雜波中的雷達(dá)目標(biāo)檢測技術(shù)綜述[J].現(xiàn)代雷達(dá),，2014,，36(12)：1-9.

[2] DONG Y.Optimal coherent radar detection in a K-distributed clutter environment[J].Iet Radar Sonar and Navigation，2012,，6(5)：283-292.

[3] HAYKIN S,，Li X B.Detection of signals in chaos[J].Proceedings of the IEEE，1995,，83(1)：95-122.

[4] HU J,，TUNG W W，GAO J.Detection of low observable targets within sea clutter by structure function based multifractal analysis[J].IEEE Transactions on Antennas and Propagation,，2006,，54(1)：136-143.

[5] LEUNG H，DUBASH N,，XIE N.Detection of small objects in clutter using a GA-RBF neural network[J].IEEE Transactions on Aerospace & Electronic Systems,，2002，38(1)：98-118.

[6] SHUI P L,，LIU M.Subband adaptive GLRT-LTD for weak moving targets in sea clutter[J].IEEE Transactions on Aerospace & Electronic Systems,，2016，52(1)：423-437.

[7] 崔少鵬.基于時頻分析的海雜波背景下目標(biāo)檢測[D].哈爾濱：哈爾濱工業(yè)大學(xué)，2014.

[8] 胡玲霞.EMD算法在雷達(dá)雜波抑制中的應(yīng)用[D].西安：西安電子科技大學(xué),，2013.

[9] 李彥兵,，杜蘭，劉宏偉,，等.基于信號特征譜的地面運動目標(biāo)分類[J].電波科學(xué)學(xué)報,，2011，32(12)：2848-2853.

[10] CHEN Z Z,，F(xiàn)AN L G,，ZHAO C，et al.Ocean wave directional spectrum measurement using microwave coherent radar with six antennas[J].Ieice Electronics Express,，2012,，19(9)：1542-1549.

[11] JIN Y，CHEN Z Z,，F(xiàn)AN L G,，et al.Spectral kurtosis-based method for weak target detection in sea clutter by microwave coherent radar[J].Journal of Atmospheric and Oceanic Technology，2015,，32(2)：310-317.

作者信息:

陳澤宗1,，2，楊  干1,，趙  晨1,，賀  超1

（1.武漢大學(xué) 電子信息學(xué)院，湖北 武漢430072,；2.武漢大學(xué) 地球空間信息技術(shù)協(xié)同創(chuàng)新中心，湖北 武漢430079）