0 引言

    在實時圖像處理,、數(shù)字信號處理等領(lǐng)域內(nèi)，經(jīng)常需要對非線性函數(shù)進行高速計算^[1],。而在人工神經(jīng)網(wǎng)絡中更是需要對大量的非線性函數(shù)進行計算,。因此，在人工神經(jīng)網(wǎng)絡的研究領(lǐng)域內(nèi),，研究如何高速地處理非線性函數(shù)具有十分重要的意義,。在人工神經(jīng)網(wǎng)絡中應用最為廣泛的是Sigmoid函數(shù)。目前對于Sigmoid函數(shù)實現(xiàn)技術(shù)的研究主要分為軟件實現(xiàn)和硬件實現(xiàn)兩個方面,。由于軟件相比硬件而言速度較慢并且并行程度很低,，所以無法滿足其快速處理的要求^[2],。因此,，在超大規(guī)模集成電路快速發(fā)展的當今時期,，研究如何利用硬件快速處理Sigmoid函數(shù)顯然更加有意義。

    FPGA憑借其可重構(gòu)技術(shù)的靈活性,，成為解決Sigmoid函數(shù)高速計算問題的有力工具,。目前利用FPGA計算Sigmoid函數(shù)常用的方法有查找表法、CORDIC算法,、Taylor級數(shù)展開法和分段線性逼近法,。查找表法^[3]提前將所有的計算結(jié)果保存在一個ROM中，這種方法計算方便且容易實現(xiàn),，但是隨著函數(shù)計算精度的提高和擬合區(qū)間的增加,，其所需求的存儲資源會顯著增加，資源消耗很高,。CORDIC算法^[4]通過多次迭代將一些復雜的運算轉(zhuǎn)換成為簡單的運算,，但是隨著精度增高，其算法的迭代次數(shù)也會提高,，計算速度會減慢,。Taylor級數(shù)展開法^[5]在精度要求較高的條件下會增加乘法器和加法器的使用，資源消耗巨大,。分段線性逼近法^[6-7]將查找表和低階多項式相結(jié)合,，計算速度較快，是當前解決此問題的主流方法,，然而在有限的分段區(qū)間用低階的多項式進行擬合運算,，其計算結(jié)果在精度上并沒有優(yōu)勢，難以實現(xiàn)高精度的運算要求,。

    為了解決上述問題,，本文采用傳統(tǒng)的分段非線性逼近法來處理Sigmoid函數(shù)。文獻[8]中使用了分段非線性逼近法來處理神經(jīng)網(wǎng)絡中常見的雙曲正切函數(shù),，然而文中并沒有給出分段方法的依據(jù),，同時在各小段的分段區(qū)間所得到的精度也差異很大。因此,，本文針對這一問題,，以Sigmoid函數(shù)為研究對象，結(jié)合Sigmoid函數(shù)自身對稱及其導數(shù)不均勻的性質(zhì),，利用數(shù)值分析中的最小二乘法作為逼近原理,，給出合理的分段方式。同時給出對比均勻分段的處理方式下逼近精度的差異情況,。利用硬件描述語言實現(xiàn)硬件結(jié)構(gòu)的設(shè)計,，并在Xilinx Virtex-5系列的XC5VLX110T器件上完成實際驗證和性能測試,，從資源使用、運算速度同計算精度等方面對設(shè)計結(jié)果進行合理評估,。

1 Sigmoid函數(shù)的分段非線性擬合方案及結(jié)果分析

    分段非線性逼近法的基本原理是用高階多項式來逼近曲線,。首先將待逼近函數(shù)按照一定的方式進行分段，之后對每一個小段構(gòu)建高階多項式近似地代替原曲線,，從而將復雜的非線性函數(shù)的計算問題轉(zhuǎn)換成為多項式的計算問題,。

    由泰勒公式的原理可知，函數(shù)在某一點按照泰勒公式展開,，隨著展開的項數(shù)越來越多,，逼近式的誤差會越來越小。并且,，隨著項數(shù)的增加,，每一項在數(shù)值上逐漸遞減，并最終趨向于無窮小,。函數(shù)在某一點按照泰勒公式展開,，保留N階多項式時，其之后的所有項數(shù)均影響誤差,，并且(N+1)階導函數(shù)的數(shù)值直接影響N階多項式的逼近結(jié)果,。具體影響的方式為：N+1階導數(shù)取絕對值后，其值越大,，表明函數(shù)在這一點處使用N階多項式逼近的誤差越高,，因此在這點處對應的分段區(qū)間間隔應該相對較小,；其值越小,，表明函數(shù)在這一點處使用N階多項式逼近的誤差越低，因此在這點處對應的分段區(qū)間間隔應該相對較大,。在考慮分段時,，可以根據(jù)N+1階導數(shù)的數(shù)值大小，將函數(shù)的分段區(qū)間進行動態(tài)調(diào)整,，避免造成誤差過大,。通過這樣的處理方式，可以對分段方式進行一些優(yōu)化,。下面結(jié)合Sigmoid函數(shù)進行具體分析,。

    首先分析Sigmoid函數(shù)及其導函數(shù)的性質(zhì)，如圖1,。F(x)為Sigmoid函數(shù),，G(x)為其4階導函數(shù)。在保證足夠的分段區(qū)間時,，使用3階多項式就能夠得到較高的逼近精度,。因此,，本文使用3階多項式逼近Sigmoid函數(shù)，4階導函數(shù)G(x)直接影響逼近的誤差,。通過研究圖像,，得出以下結(jié)論：

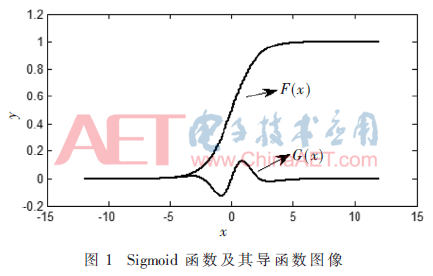
    (1)Sigmoid函數(shù)F(x)是以點(0，0.5)為對稱中心的函數(shù),，因此在計算Sigmoid函數(shù)值時只需計算正區(qū)間或負區(qū)間,，另一半可通過對稱關(guān)系得到,；

    (2)以正區(qū)間為研究對象,，Sigmoid函數(shù)的4階導數(shù)在x=1處附近取得最大值，并向兩側(cè)衰減,，隨著x的不斷增大,，4階導數(shù)最終趨向于0。

    為了驗證這種基于導數(shù)的分段方法在逼近結(jié)果的精度方面是否具有優(yōu)勢,，本文選擇了將這種分段方式與傳統(tǒng)的等間距分段方式作對比,。首先，將Sigmoid函數(shù)的待處理區(qū)間進行等分,，之后比較每個子區(qū)間的函數(shù)4階導數(shù)的整體變化規(guī)律,，對導數(shù)相對較大的區(qū)間進行縮短，對導數(shù)相對較小的區(qū)間進行擴展,。分別對這兩種分段方式下所有的子區(qū)間構(gòu)建3階多項式,，通過對比函數(shù)各子區(qū)間及整體區(qū)間的誤差情況來驗證此分段方法的優(yōu)勢。

    本文選用MATLAB作為函數(shù)擬合工具,，構(gòu)建擬合多項式使用最小二乘法原理,，數(shù)據(jù)類型選取雙精度浮點數(shù)，這樣可以保證在計算過程中精度比較高,。下面分別給出兩種分段方式下的分段結(jié)果及誤差對比,。為了保證實驗結(jié)果可靠，各分段區(qū)間取的數(shù)足夠大(這里以0.000 1為間隔取數(shù)),，結(jié)果見表1,。

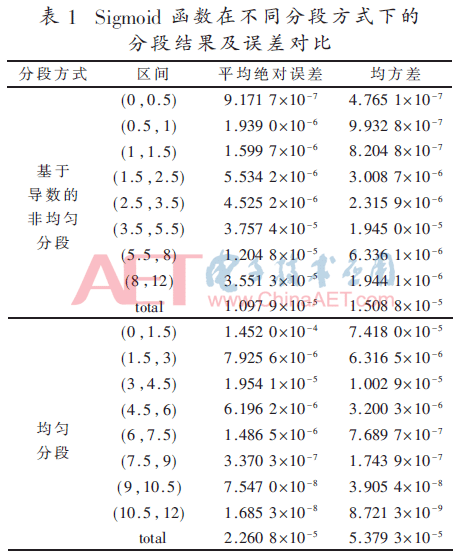
    通過表1可以得出，當使用三階多項式對Sigmoid函數(shù)進行逼近時,，參照4階導函數(shù)的數(shù)值而分段的處理方式在平均絕對誤差和均方差兩項指標上均優(yōu)于等間距分段的處理方式,。從整體區(qū)間上看，平均絕對誤差減小了51.4%,，均方差減小了71.9%,。

2 Sigmoid函數(shù)的FPGA實現(xiàn)

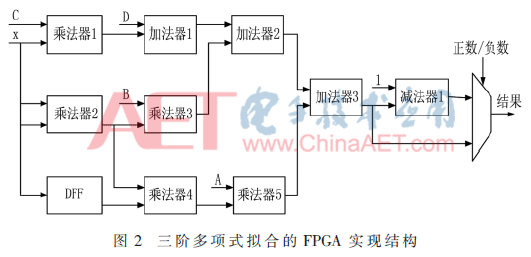
    為了實現(xiàn)高精度的擬合要求，本文采用表1中基于導數(shù)的分段方式,，使用三階多項式對Sigmoid函數(shù)進行擬合處理,，并給出其FPGA實現(xiàn)結(jié)構(gòu),，如圖2所示。設(shè)三階多項式為y=Ax³+Bx²+Cx+D,，其在FPGA中的計算流程為：

    (1)取系數(shù),。各分段區(qū)間下的系數(shù)A、B,、C,、D預先存儲在RAM中，通過輸入x取出與之對應的系數(shù)A,、B,、C、D,。

    (2)計算Cx和x²,。

    (3)計算Cx+D、Bx²和x²,。

    (4)計算Bx²+Cx+D和Ax³,。

    (5)計算Ax³+Bx²+Cx+D。

    (6)用1和步驟(5)的結(jié)果做減法,。

    (7)選擇器,。當輸入的x為非負數(shù)時，輸出為步驟(5)的結(jié)果,；若輸入的x為負數(shù),，輸出為步驟(6)的結(jié)果。

    上述所有的乘法器,、加法器和減法器的設(shè)計采用Xilinx公司提供的32位單精度浮點型IP核實現(xiàn),，整個算法采用了流水線結(jié)構(gòu)，數(shù)據(jù)輸入后,，10個周期延遲后得到計算結(jié)果,。具體實驗數(shù)據(jù)如表2所示。

    在實驗過程中,，表1的誤差結(jié)果是由算法在FPGA上計算得到的結(jié)果與Sigmoid函數(shù)的真實值(精度遠高于實驗的精度)之間的對比求得的,。表2中的誤差結(jié)果與表1中的誤差結(jié)果相比較在平均絕對誤差方面略有不足，是由于在FPGA中使用的32位單精度浮點數(shù)在精度上不同與MATLAB上使用的64位雙精度浮點數(shù),，所以兩者之間存在略微差別,，然而并不影響算法的準確性。

    采用基于導數(shù)的分段方式并使用三階多項式的擬合方案在FPGA上所使用的資源雖然比經(jīng)典的CORDIC算法及分段線性逼近方法較多,，然而這種擬合方案在算法的精度上達到了10^-5數(shù)量級,，各小段分段區(qū)間甚至達到10^-6數(shù)量級。當然,，采用更高階數(shù)的多項式逼近在理論上能夠?qū)崿F(xiàn)更高的精度,，然而這樣的代價是會消耗更多的硬件資源,。本文使用的分段非線性逼近法對Sigmoid函數(shù)的處理結(jié)果上，精度遠遠大于另兩種算法在現(xiàn)有的文獻中所取得的精度,。并且若要達到較高精度,，CORDIC算法會大大的增加迭代次數(shù)從而降低運算速度，分段線性逼近則會大大的增加存儲資源,。

3 結(jié)論

    本文針對人工神經(jīng)網(wǎng)絡中應用最為廣泛的Sigmoid函數(shù),，采用傳統(tǒng)的分段非線性逼近方法，結(jié)合Sigmoid函數(shù)自身對稱的性質(zhì)及其導數(shù)不均勻的特點,，給出合理的分段方式,，在各小段分段區(qū)間內(nèi)使用數(shù)值分析中經(jīng)典的最小二乘法作為擬合逼近原理，得出初始分段間距同逼近多項式的階數(shù)對擬合結(jié)果精度的影響,。按照上述方法給出一種在精度上達到了10^-5數(shù)量級的Sigmoid函數(shù)的擬合方案,，實現(xiàn)了現(xiàn)階段對Sigmoid函數(shù)的高速、高精度的處理要求,。

參考文獻

[1] JAIN V K，LIN L.High-speed double precision computation of nonlinear functions[C]//Symposium on Computer Arithmetic.IEEE Computer Society,，1995：107.

[2] MOLZ R F,，ENGEL P M，MORAES F G,，et al.Codesign of fully parallel neural network for a classification problem[J].

[3] LEBOEUF K,，NAMIN A H，MUSCEDERE R,，et al.High speed VLSI implementation of the hyperbolic tangent sigmoid function[C]//International Conference on Convergence and Hybrid Information Technology.IEEE,，2008：1070-1073.

[4] 萬書芹，陳宛峰,，黃嵩人,，等.基于改進CORDIC算法實現(xiàn)高速直接數(shù)字頻率合成器[J].儀器儀表學報，2010,，31(11)：2586-2591.

[5] OUALI J,，SAUCIER G.Fast generation of neuro-ASICs[M]//International Neural Network Conference.1990.

[6] ARMATO A，F(xiàn)ANUCCI L,，SCILINGO E P,，et al.Low-error digital hardware implementation of artificial neuron activation functions and their derivative[J].Microprocessors & Microsystems，2011,，35(6)：557-567.

[7] BASTERRETXEA K,，TARELA J M，DEL CAMPO I.Digital design of Sigmoid approximator for artificial neural networks[J].Electronics Letters,，2002,，38(1)：35-37.

[8] XIE Z Z,，ZHANG S Y.A non-linear approximation of the sigmoid function based FPGA[M]//Proceedings of the 2011，International Conference on Informatics,，Cybernetics,，and Computer Engineering(ICCE2011) November 19-20，2011,，Melbourne,，Australia.Springer Berlin Heidelberg，2011：221-223.

作者信息：

宋宇鯤,，高曉航,，張多利，杜高明

(合肥工業(yè)大學 微電子設(shè)計研究所,，安徽 合肥230009）