0 引言

    慣性傳感器作為慣性導航系統(tǒng)中的核心部件,，其精度直接影響到整個慣導系統(tǒng)的性能。隨著科學技術不斷發(fā)展,，對精度要求越來越高^[1],，因此，如何提高慣性傳感器精度是長期以來的研究重點,。目前主要通過濾波的方式提高慣性傳感器的精度,。傳統(tǒng)處理方法有小波分析和卡爾曼濾波^[2-3]等。這些方法均從變換域表示來獲取信號的屬性,，針對特定類型的特定信號取得較好的效果,，不具有普遍性。近年來,，稀疏性問題隨著壓縮感知理論^[4]的提出得到了系統(tǒng)性的研究,，并運用于信號去噪領域。由于大部分信號在變換基下是稀疏的,，所以該方法得到廣泛的應用,。文獻[5]通過K-VSD算法訓練獲得冗余字典，再利用稀疏表示實現(xiàn)慣性傳感器信號濾波,，不過原子庫數(shù)目巨大,。此外，基于稀疏分解理論的主要重構方法是正交匹配追蹤算法(Orthogonal Matching Pursuit,，OMP)^[6],，但運行時間較長。壓縮采樣匹配追蹤算法^[7]雖然改善了重構速度,，但要求在給定迭代次數(shù)的條件下進行,，且需已知信號的稀疏度。目前,，隨著智能算法的興起,，文獻[8]提出人工蜂群與MP重構算法結合，通過模擬蜂群采蜜以加速最優(yōu)化進程,，不過該算法更新公式單一,，易陷入局部最優(yōu),。遺傳算法與重構算法結合^[9]相繼提出，交叉,、變異等遺傳算子很好地豐富了種群,，但所需種群數(shù)多，收斂速度慢,。

    針對現(xiàn)有算法的缺陷,，本文提出將免疫量子進化與OMP相結合來實現(xiàn)慣性傳感器信號重構,。該算法無需已知信號稀疏度,，通過免疫機制中的免疫操作，不斷增加抗體對抗原的親和度,，從而找到最優(yōu)解,。算法中，量子搜索機制可有效防止算法后期的退化現(xiàn)象,，加快OMP算法的收斂速度,。引入免疫機制使量子進化算法具有更強的全局搜索能力，不易陷入局部最優(yōu)狀態(tài),，并有效保證了信號的重建速度和精度,。

1 算法理論

1.1 量子進化算法理論

    量子進化算法^[10]是一種基于量子計算原理的優(yōu)化方法。該算法以量子計算為基礎,引入量子比特編碼和量子門,。量子比特編碼是用量子態(tài)矢量表示染色體,，一條染色體能表達為多個態(tài)的疊加。量子門使種群得到更新,，保證收斂性,。所以量子進化與經(jīng)典遺傳算法相比，擁有豐富的多樣性特征和較好的收斂性,。

    量子狀態(tài)用量子比特表示,，與經(jīng)典比特不同之處在于疊加態(tài)的存在，它可以落在|0>和|1>之外的線性組合態(tài),。量子位狀態(tài)用下式表示：

1.2 OMP算法原理

    當信號長度有限時,，隨著k值的不斷增大，信號殘余的能量將以指數(shù)形式遞減,，最后收斂到0,。

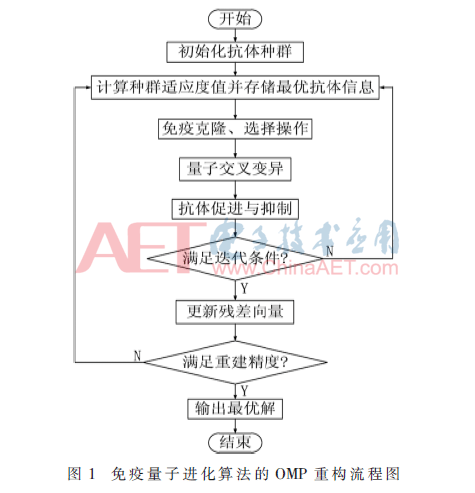
2 免疫量子進化算法的OMP重構方法

    將免疫量子進化算法與OMP重構結合用于慣性傳感器信號，通過構建與信號特征相匹配而與噪聲信號不相關的匹配原子,，組成過完備原子庫,。先在庫中通過免疫操作和量子操作來加速最佳匹配原子搜索進程，提取與信號最匹配的原子,；然后選取最大迭代次數(shù)作為迭代的終止條件,，避免因迭代次數(shù)選取不當,，影響處理效果；最后利用各次迭代提取的最佳匹配原子完成慣性傳感器信號的重構,，進而實現(xiàn)信號濾波,。算法中以原子庫作為種群、原子庫的一個原子的參數(shù)組作為抗體,，尋找適應度大的抗體作為優(yōu)化目標,，信號在原子庫的投影值則為適應度函數(shù)值。 

2.1 改進策略

    本算法將量子搜索機制和免疫算法的克隆選擇原理相結合,，利用量子編碼的疊加性構造抗體,；通過克隆操作產(chǎn)生原始種群和子種群以實現(xiàn)種群擴張，提高了局部搜索能力,，同時借助量子交叉操作避免陷入局部最優(yōu),。基于克隆算子的基本框架,，采用量子編碼來表示抗體,，設計針對量子編碼的量子非門變異，并構造具有量子特性的多點交叉策略,。

2.2 免疫操作

    克?。翰捎幂啽P賭方法確定克隆產(chǎn)生的子種群規(guī)模。設克隆前種群為Q={q₁,，q₂,，…，q_N},，N為種群規(guī)模的大小,，克隆操作后的種群為Q′={Q，C},，其中C為克隆產(chǎn)生的抗體子群,。克隆規(guī)模主要依據(jù)抗體-抗原適應度,，抗體中的相對大小可自適應調(diào)整,，即抗體受抗原的刺激時，克隆規(guī)模的多少依據(jù)其影響的大小來確定,。公式如下： 

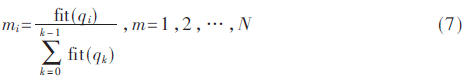
式中,，m_i為種群中第i個抗體的克隆規(guī)模，fit(q_i)為第i個抗體-抗原的親和度,，即抗體i的適應度值,。

    選擇：從克隆操作后的種群中選擇優(yōu)秀的抗體，形成新的種群,。即通過計算適應度函數(shù)值選擇最佳抗體集合,，進而組成最優(yōu)解集合,。

2.3 量子操作

    將抗體進行變異，即利用概率變異重新計算新抗體的適應度值,，將一定數(shù)量親和度高的解作為優(yōu)秀抗體,。

    量子交叉：本文采用多點交叉。即：選出相互配對的兩個抗體,，隨機設置多個交叉點,，然后以交叉概率互換抗體中交叉點之間的基因以增加種群多樣性。

2.4 抗體促進與抑制

    計算種群中抗體的適應度值,，并對種群中的抗體兩兩進行比較,，將適應度值大的抗體替換適應度值低的抗體，以達到抗體的促進與抑制效果,。

2.5 計算種群適應度

    本文算法在搜索最優(yōu)抗體的過程中,，不依賴任何外部信息,，僅以種群內(nèi)部各個抗體的適應度函數(shù)值為線索進行搜索,。文中定義信號或信號殘余R_kf與原子的內(nèi)積絕對值|<R_kf，g_γk>|為適應度函數(shù),，記為Y_k:Y_k=arg|<R_kf,，g_γk>|(k=1，2,，…,，N)。

2.6 算法步驟

    設Gabor原子庫矩陣為M×N列,，將該矩陣的N列作為N個抗體,，每個抗體具有1個量子比特位，M個量子態(tài),，其中N個量子比特表示矩陣的N列,，每個量子態(tài)表示矩陣的每個元素。步驟如下：

2.7 實時處理方法

3 仿真與結果分析

3.1 靜態(tài)數(shù)據(jù)的驗證

    首先用慣性傳感器靜態(tài)觀測數(shù)據(jù)驗證算法,。通過引入信噪比,、均方誤差、標準差(零漂值)和處理時間對降噪效果進行評估,。其中,，均方誤差為參數(shù)估計值與真實值之差平方的期望值，以衡量平均誤差,。仿真信號為某光纖陀螺(FOG)靜態(tài)輸出信號的實際采樣,，采樣頻率為5 000 Hz，信號長度N=300,。設算法中交叉概率為0.85,，變異概率為0.1,，最大迭代次數(shù)為20。其中,，以小波濾波后的信號作為該光纖陀螺的真實信號,。經(jīng)本文算法處理后的效果如圖2所示。

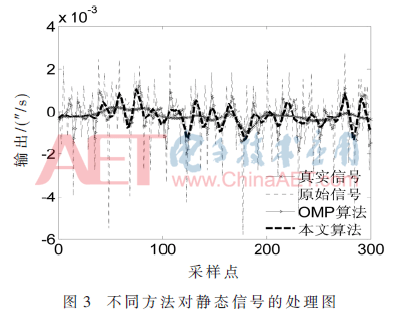
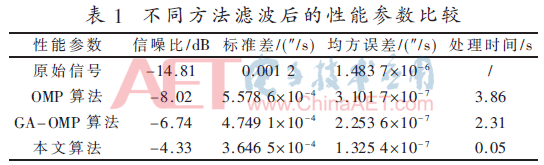
    為了便于比較,，將該算法與OMP及GA-OMP算法（遺傳算法的OMP重構）在相同的實驗環(huán)境下進行相同參數(shù)的實驗,。限于篇幅，僅列出OMP算法與本文算法的效果對比圖,，仿真結果如圖3所示,。統(tǒng)計同一靜態(tài)信號處理后的性能參數(shù)，具體數(shù)據(jù)如表1所示,。由表1可知,，靜態(tài)信號經(jīng)本文算法處理后，性能參數(shù)均優(yōu)于OMP及GA-OMP算法,，且無需事先已知信號稀疏度,。綜合表1和圖3可得，慣性傳感器信號的實際靜態(tài)信號中含有的噪聲能量遠大于真實信號,，輸出的零偏和波動性較大,。經(jīng)實驗驗證，OMP算法處理后,，單點信號處理時間為12.8 ms,，大于系統(tǒng)要求的0.2 ms(采樣頻率為5 000 Hz)，不能進行實時處理,。本文算法與OMP算法相比,，處理后信號信噪比提高3.69 dB，零漂值降低1.932 1×10^-4(″/s),，均方誤差降低1.776 3×10^-7(″/s),。比原信號信噪比提高了10.48 dB，標準差降低了8.353 5×10^-7(″/s),，均方誤差降低了1.351 2×10^-6(″/s),，且單點信號處理時間為0.166 ms，達到實時處理要求,。實驗結果表明,，本算法大大縮短信號處理時間的同時，改善了零漂值,，提高了信號處理精度,，故驗證了算法對慣性傳感器靜態(tài)信號的有效性。

3.2 對動態(tài)數(shù)據(jù)的驗證

    利用動態(tài)數(shù)據(jù)進一步驗證算法的可行性。仿真信號為：通過高頻濾波器取出某光電跟蹤系統(tǒng)輸出高于500 Hz的實際FOG信號,，作為噪聲疊加到正弦信號上,。正弦信號頻率為128 Hz，疊加的信號采樣頻率為5 000 Hz,，信號長度N=300,。其他參數(shù)與靜態(tài)信號一致。本文算法處理后效果如圖4所示,。

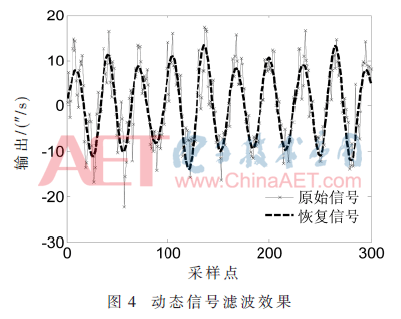
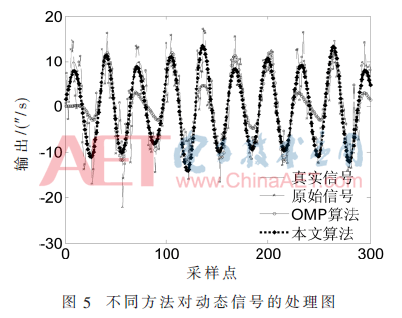
    圖5為相同實驗環(huán)境和參數(shù)設置下OMP算法與本文算法的效果圖,。表2為本文算法與OMP及GA-OMP算法對同一動態(tài)信號處理后的性能參數(shù)比較。動態(tài)信號不存在零漂值,，故不列出,。由表2可知，本文算法在動態(tài)數(shù)據(jù)仿真測試下,，性能仍優(yōu)于OMP及GA-OMP算法,。經(jīng)實驗驗證，OMP算法處理后的時間為4.18 s,，不能滿足實時處理要求,。經(jīng)本文算法處理后，與OMP算法相比,，信號信噪比提高了6.2 dB,，均方誤差降低了25.878 (″/s),。比原始信號信噪比提高了7.55 dB,，均方誤差降低了28.551(″/s)。有效改善了信號輸出精度的同時,，信號單點處理時間為0.133 ms,，滿足實時處理要求，因此,，驗證了算法對動態(tài)信號處理的有效性,。

4 結論

    本文根據(jù)慣性傳感器信號的特點，將免疫機制引入量子進化算法對OMP重構算法進行改進,，并將其應用于慣性傳感器輸出信號的實時處理,。由仿真結果可知，在信號稀疏度未知的情況下,，所提出的算法對慣性傳感器的靜態(tài)和動態(tài)數(shù)據(jù)均能在加快信號處理的同時提高濾波性能,，為慣性傳感器信號提供了實際應用價值和廣泛的應用前景。

參考文獻

[1] 許江寧,，朱濤,，卞鴻巍.慣性傳感技術與展望[J].海軍工程大學學報，2007,，19(3)：1-5.

[2] 郭曉松,，張東方,，薛海建，等.基于小波去噪和TLS算法的全姿態(tài)尋北[J].系統(tǒng)工程與電子技術,，2016,，38(2)：362-367.

[3] 戴冬冰.基于卡爾曼濾波的陀螺儀數(shù)據(jù)處理[J].數(shù)字技術與應用，2014(5)：119-121.

[4] BOUGHER B.Introduction to compressed sensing[J].The Leading Edge,，2015,，34(10)：1256-1257.

[5] 蔣行國，張龍,，許金海.一種基于稀疏表示的慣性傳感器信號實時濾波方法[J].計算機應用研究,，2015，32(5)：1480-1482.

[6] WU R,，HUANG W,，CHEN D R.The exact support recovery of sparse signals with noise via orthogonal matching pursuit[J].IEEE Signal Processing Letters，2013,，20(4)：403-406.

[7] HUANG F,，TAO J，XIANG Y,，et al.Parallel compressive sampling matching pursuit algorithm for compressed sensing signal reconstruction with OpenCL[J].Journal of Systems Architecture,，2016，27(1)：51-60.

[8] 侯坤,，易正俊,，何榮花.信號稀疏分解的人工蜂群-MP算法[J].計算機仿真，2012,，29(11)：247-250.

[9] 王國富,，張海如，張法全,，等.基于改進遺傳算法的正交匹配追蹤信號重建方法[J].系統(tǒng)工程與電子技術,，2011，33(5)：974-977.

[10] CAO G L,，HU R,，QIAN B.Effective hybrid quantum evolutionary algorithm for capacitated vehicle problem[J].J Comp Inte Manu Syst，2015,，21：1101-1113.

作者信息：

蔣行國1,，2，羅珍珍1,，李海鷗1,，2，歐少敏3

(1.桂林電子科技大學 信息與通信學院，廣西 桂林541004,；

2.桂林電子科技大學 廣西精密導航技術與應用重點實驗室,，廣西 桂林541004；

3.桂林電子科技大學 信息科技學院,，廣西 桂林541004）