0 引言

    公鑰密碼體制以其獨特的理論依據(jù)很好地填補了密碼領域的空缺。它在密鑰分發(fā),、身份認證等方面具有明顯優(yōu)勢,。1985年Neal Koblitz和Victor Miller分別獨立提出了橢圓曲線在密碼學中的應用。作為三大公鑰密碼體制之一,，橢圓曲線密碼體制具有相同粒度更難破解,、單位比特安全強度更大的特點。

    橢圓曲線密碼運算在底層結構設計時,，主要包括模加減,、模乘和模除,、模逆。其中,，模除和模逆運算最為復雜,，通常通過轉換運算坐標來降低其實現(xiàn)復雜度，且使用頻率不是很高,。而模乘和模加減運算使用更為頻繁,。如何高效率、低成本地實現(xiàn)模乘模加減是當前的一個研究熱點,。1985年Montmery提出了一種全新的模乘算法,，他將普通模乘的運算轉換到Montgomery剩余類中進行，其所有大數(shù)均規(guī)約到了剩余類中,，計算大幅度簡化,。Montgomery模乘算法是目前最為常見的模乘實現(xiàn)方法，但傳統(tǒng)的算法具有算法粒度固定,、關鍵運算路徑過長的缺陷,，而且不支持雙有限域運算。文獻[2]提出了一種Montgomery模乘算法在高基陣列上的優(yōu)化算法,。文獻[3]提出了一種基于CIOS模乘的可重構可伸縮的雙域模乘加器,，將模乘與模加減糅合，但面積不夠優(yōu)化,。文獻[4]提出了一種改進的基于FIOS類型Montgomery雙域模乘器,，流水線切割較為合理。本文在前人的研究基礎上,，通過對雙域模乘和模加減單元進行分析,，以FIOS算法為基礎，重新設計了一種MAS（multiplication- addition-subtraction）結構,，將模乘和模加減進行可重構糅合,，一定程度上降低了單元面積，又可以靈活地適配各種長度的模運算,，從而適應各種不同的應用場景和任務,。同時對模乘的關鍵運算路徑進行了流水線設計，相對于傳統(tǒng)的模乘算法,，運算頻率有一定的提高,。

1 模乘加算法分析

    模乘、模加減和模逆運算構成了ECC密碼算法中的主體運算,。設計模乘模加減功能復用的模乘加單元結構,，可以提高結構利用率，減少多余連線資源，進而降低總體面積,。本文對雙域模加減算法及雙域模乘算法進行了分析,。根據(jù)兩者運算的原理可知，模乘對模加減無論是在算法層次還是結構層次上具有較為完整的兼容性,。兼容關系如圖1所示,。

    本文針對現(xiàn)有模乘和模加算法進行改進，設計了如下所示的模乘加算法,。

    算法1 適于硬件實現(xiàn)的FIOS模乘加改進算法

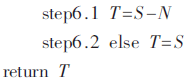
    算法將輸入的大整數(shù)A,、B、N按照32 bit字長進行分解運算^[4],，字數(shù)為s，算法具有內外兩層循環(huán),，對操作數(shù)按32 bit字長進行循環(huán)掃描,，其中內循環(huán)完成32 bit數(shù)據(jù)的乘和64 bit的加法運算，外循環(huán)完成對被乘數(shù)的遍歷掃描,。算法在GF(2ⁿ)域與GF(p)域上實現(xiàn)過程大致相同,，區(qū)別在于GF(2ⁿ)域上的加法是異或操作，乘法則為多項式乘法,，并且循環(huán)結束后直接輸出結果,，而不需要與不可約多項式進行比較。

    算法初始有一個信號a,，用于判斷運算模加減或者模乘,。如果a=0進入step2運行模乘，否則進入step5運行模加減,，而此時的加法不再是模乘中的64 bit加,，而是3個64 bit加的級聯(lián)，即為192 bit加,。此處即為本文提出的模乘模加糅合結構的關鍵所在,。運算過程有3個for循環(huán)，其中前兩個是嵌套在一起內外循環(huán),。設計的流水運算單元也是主要用來完成這部分嵌套循環(huán),。在硬件設計過程中step2.2、2.3,、2.4作為一部分結構Y,。step2.5.1、2.5.2,、2.5.3,、2.5.4作為重復的結構X出現(xiàn)在硬件結構中。

    為了更加清晰描述算法中數(shù)據(jù)的傳遞與處理過程，列出了FIOS模乘器流水樹結構,，其中X與Y分別對應上文提到的結構X與結構Y(Y結構包括PreY與Y兩個操作),。每一橫行表示同一時鐘周期參與運算的單元，每一豎列表示下一時鐘周期數(shù)據(jù)傳遞方向,。圖2描述的是前n個時鐘周期數(shù)據(jù)運算傳遞,。

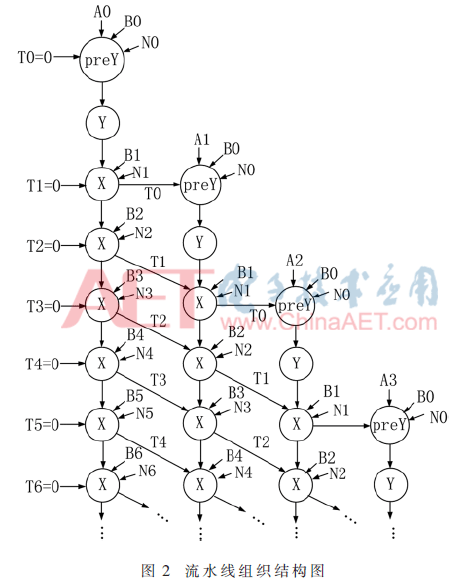
2 可編程FIOS模乘加器電路設計

2.1 模乘加器總體結構設計

    模乘運算電路是該設計的核心，本文設計的模乘單元數(shù)據(jù)路徑位寬為192 bit,，通過迭代,，可以完成576 bit以內任意比特的雙有限域模乘運算。該模乘加數(shù)據(jù)路徑核心為處理單元Y,、N個處理單元X和模加減單元,，其中Y結構由兩部分構成，詳見流水線結構設計,。具體結構如圖3所示,。模加減單元中的兩個虛線ADDER192 bit，表示其由MA X#N和MA X#N-1的相關結構替代,。

    雙域模乘加器主要由數(shù)據(jù)輸入,、數(shù)據(jù)輸出、狀態(tài)機控制,、模乘運算,、模加減運算等單元構成。

    數(shù)據(jù)輸入輸出單元負責對數(shù)據(jù)進行整合以及與外界的數(shù)據(jù)對接,。其中輸出單元需要根據(jù)運算域的不同改變輸出模式,。

    狀態(tài)機控制單元完成整個可重構向量模乘加單元運算時對各個模塊的調度控制。根據(jù)輸入的運算選擇信號及數(shù)據(jù)的長度,，判斷進行模乘還是模加減,，二元域還是素數(shù)域，以及進行模乘的輪數(shù)和,。

    由于算法1在實現(xiàn)中存在較高的內部并行性,，因此模乘運算模塊可以采用多個并列處理單元來組成線性陣列流水線結構實現(xiàn)算法提速，也就是上文提到的N個處理單元X的結構,。

2.2 雙域模乘加糅合部分設計

    圖4是模加減器結構示意圖,。有兩個可重構的向量加法運算單元。

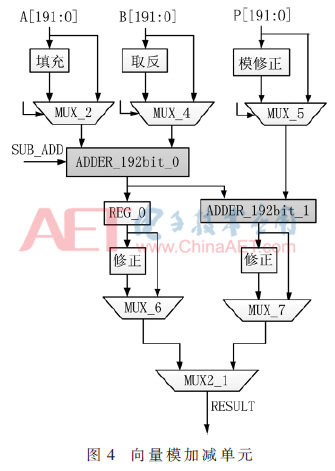
    向量模加減單元的核心是一個位寬為192 bit能夠進行雙有限域加減法運算的加法器,。當數(shù)據(jù)長度不超過192 bit時,，數(shù)據(jù)路徑?jīng)]有反饋情況；當大于192 bit時,，則在控制電路的調度下循環(huán)反饋多次運算,。該192 bit加法器由6個32 bit可重構字加法器組成。其中，每個字加法器可以執(zhí)行兩個有限域上的加減法運算,，且通過級聯(lián)方式完成192 bit數(shù)據(jù)的運算,，如圖5所示。每個字加器無需等待上一級進位才進行運算,，而是預先對兩種進位情況分別進行計算,，得到兩種不同的結果。當前一級進位到達時,，由進位信號進行結果選擇,。若計算數(shù)據(jù)的長度超過192 bit，則需要將第六級字加法器的進位返回至第一級字加法器,，進行下一循環(huán)的計算,。圖6中DFA為雙有限域加法器。

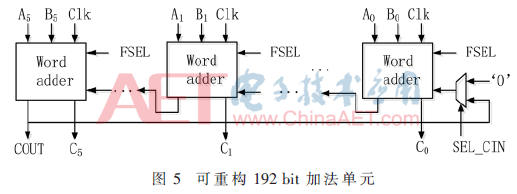
    圖7是模乘單元的MA X#1到MA X#N-2的結構,。對應于算法的step2.6,。不過，它將T_j+A_i×B_j與C+mN_j并行計算,，而且還有T_j-1+A_i×B_j-1與C+mN_j-1進行相加的單元。

    圖7結構包含3個64 bit的加法器,，如果進行級聯(lián),，并加入進位判斷電路，即可完成模加模塊所需的192 bit加法運算,。如圖8所示,，即為加入級聯(lián)結構的MA X#N-1和MA X#N的結構?？梢酝瑫r滿足模乘與模加的運算需求,。其中的ADDER64是由進位為0或1的兩個32 bit加法器級聯(lián)構成的，即運用了上文中可重構字加器的設計方法,。

2.3 流水線單元設計

    該模乘加器的流水加速設計主要體現(xiàn)在模乘器的嵌套循環(huán)結構上,。如圖9所示。該流水線單元主要由3部分構成,，分別是：移存器,、處理單元Y（由preY、Y構成）,、處理單元X,。其中，移存器完成A,、B,、N的字輸入；Y單元完成算法中的step2.2、2.3,、2.4,；X單元用于完成step2.5.1、2.5.2,、2.5.3,、2.5.4的循環(huán)。N個X單元可以滿足576 bit以內的任意比特模乘運算,，以下是針對7個X的結構分析,。其合理性將在后文進行分析。

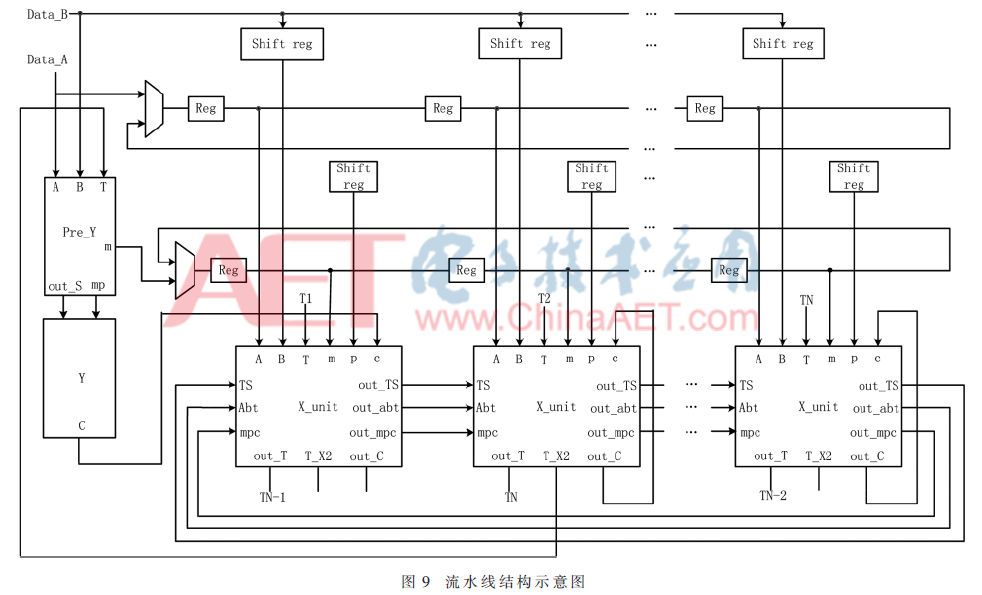
    狀態(tài)機產(chǎn)生控制信號,，驅動移存期,，為每個單元提供相應的數(shù)據(jù)字，數(shù)據(jù)A首先通過Y結構進行6個時鐘周期的運算完成前兩個字Ai與B0的乘法,，而后傳輸?shù)絏單元中,，并根據(jù)參加模乘數(shù)據(jù)的長度，進行對應輪數(shù)的X單元運算,，而后以字為單位輸出運算結果,。下面對長度分別為192 bit、384 bit,、576 bit的數(shù)據(jù)運算過程進行分析,。

    (1)參加模乘運算數(shù)據(jù)為192 bit時，即6個字,。根據(jù)結構設計,，A_i與B₀在外循環(huán)中進行，X單元本級運算的數(shù)據(jù)T_j+A_i×B_j與C+mN_j傳到下一級使用(詳見硬件結構設計),，因此需要經(jīng)過6個X單元的運算才能完成數(shù)據(jù)的輸出,。最終最低字T₀在X₂中輸出，最高位T₅在X₇中輸出,。數(shù)據(jù)進入X單元后,，需要經(jīng)過兩個周期才能輸出。因此從第一個有效數(shù)據(jù)A₁進入X₁開始,，第3個周期產(chǎn)生T₀,；第6個周期，第二個有效數(shù)據(jù)A₂進入X₁,。即此時A₁和B的乘法與A₀和B的乘法并行運行,。第12個周期，第一輪的中間T₁生成,，之后以此類推,。 

    (2)參加模乘運算數(shù)據(jù)為384 bit時,，即12個字。同192 bit運算,，需要經(jīng)過12個X單元才能完成一輪內循環(huán),。不過在X₇完成運算時需要數(shù)據(jù)再次傳送回X₁繼續(xù)進行循環(huán)，且此時恰巧Y單元沒有數(shù)據(jù)輸入到X₁單元（Y單元每6個時鐘周期更新一次B_i值,。并不是每個周期都為X單元提供數(shù)據(jù)）,。X單元運算需要2個時鐘周期，7次運算則需要14個時鐘周期,。而Y單元需要6個時鐘周期才會往X₁中輸入數(shù)據(jù),，14個時鐘正介于12到18時鐘周期之間，因此不會出現(xiàn)數(shù)據(jù)輸入沖突,。該結構包含7個X處理單元,，可以避免576 bit以內乘法運算均不出現(xiàn)數(shù)據(jù)沖突。

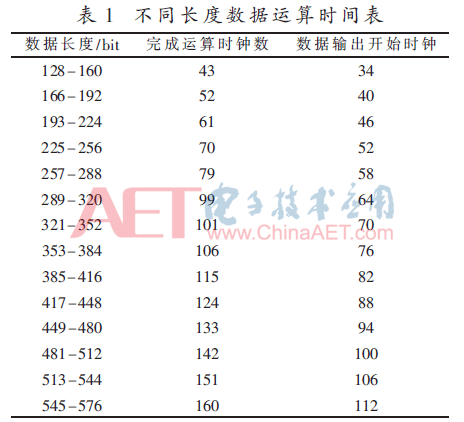
    (3)參加模乘運算數(shù)據(jù)為576 bit時,，即18個字,。同理，需要經(jīng)過18個X單元才能完成一輪內循環(huán),，要在第三輪的X₄處完成第一次循環(huán)運算,。而此時，7個X單元里面進行的是不同的內循環(huán),，比如第40個時鐘周期（從有效數(shù)據(jù)輸入Y開始計算時鐘）,，X₁到X₇分別在進行A₁×B₁₄、A₃×B₈,、A₅×B₂、A₀×B₁₇,、A₂×B₁₁,、空（X₇此時無有效運算）的內循環(huán)。其中,，A_i×B_j表示A的第i個字與B的第j個字相乘,。對應算法step2.5.1 H_j=T_j+A_iB_j，I_j=mN_j+C,，及本輪內循環(huán),。表1是具體的運算數(shù)據(jù)表格。

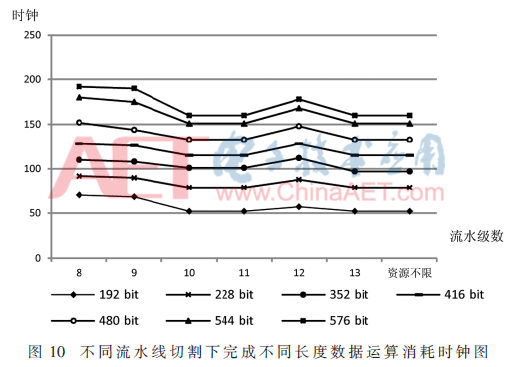
    下面對不同級流水結構進行分析,。圖10是不同的流水線結構下完成不同長度運算用時折線圖,。由折線圖可知，到10級流水線結構之后,，再次增加X單元的數(shù)量運算周期不再降低,，反而會使面積增大,，降低單元的整體利用率。因此在綜合了面積,、運算效率及單元利用率方面因素后,，最終決定采用10級流水結構，其中Y內部有三級流水,，7個X對應7級,。

3 性能分析

    本文采用了Verilog HDL對設計進行了RTL級描述，對設計進行功能仿真驗證,，并在0.18 μm CMOS工藝標準單元庫下對可重構模乘單元進行邏輯綜合,，綜合工具使用Synopsys公司的Design Complier。綜合結果表明,，可重構模乘加單元占用面積927 312 μm²,，最大延遲4.3 ns，最高時鐘可達到230 MHz,。由于沒有同類別的可重構的模乘加單元可供比較且電路的綜合環(huán)境和仿真平臺不同,，因此只與其他一些國內外先進設計文獻中模乘器的性能進行比較。表2列出了本文與其他文獻的模乘運算單元的性能比較,。

    由于模乘加結構的關鍵路徑存在于模乘模塊中,，性能指標里面主要進行模乘方面的性能比較。與文獻[3]比較,，雖然速度略有差距,，但是面積具有很大優(yōu)勢。與文獻[4]比較,，雖然面積略有劣勢,，但是支持雙域運算且運算位寬范圍更廣。與文獻[5],、文獻[7]的設計相比,，本文提出的結構單元在運算速度和面積方面均有優(yōu)勢。綜合比較,，本設計在功能及性能上具有較強的綜合優(yōu)勢,，并且可以適應于各種不同的場合和任務。

4 結論

    本文提出了基于FIOS算法和可重構模加減算法的雙域可伸縮模乘加算法,。并運用了10級流水線結構,，設計了支持576 bit以內的任意長度雙域可重構模乘加減運算單元。在結構上很好地完成了模乘與模加減的單元公用,，提高了單元的利用率,。為模乘加單元的設計提供了一定的參考。

參考文獻

[1] 仲先海.并行可配置ECC協(xié)處理器關鍵技術研究[D].鄭州：信息工程大學,，2008.

[2] 胡進,，何德彪,，陳建華.基于高基陣列乘法器的高速模乘單元設計與實現(xiàn)[J].計算機工程與設計，2010,，31(6)：1202-1204.

[3] 王威,，嚴迎建，易衛(wèi)兵.雙域可重構CIOS模乘加器研究與設計[J],微電子學,，2015,，45(4)：502-506.

[4] 楊曉輝，王雪瑞,，秦帆.基于FIOS類型的Montgomery雙域模乘器設計[J].電子技術應用,，2011，37(10)：144-149.

[5] 郭曉,，蔣安平,，宗宇.SM2高速雙域Montgomery模乘的硬件設計[J].微電子學與計算機，2013,，30(9)：17-22.

[6] 史焱,，吳行軍.高速雙有限域加密協(xié)處理器設計[J].微電子學與計算機，2005,，22(5)：8-12.

[7] Akashi Satoh,，Kohji Takano.A scalable dual-field elliptic curve cryptographic processor[J].IEEE.Transactions on Computers， 2003,，52(4)：449-460.

[8] KOC C K,，ACAR T.Analyzing and comparing montgomery multiplication algorithms[J].IEEE，Micro,，1996,，16(3)：26-33.

[9] SATOH A，TAKANO K.A scalable dual-field elliptic curve cryptographic processor[J].IEEE.Transactions on Computers,，2003,，52(4)：449-460.

[10] NEDJAH N，MOURELLE L M.Three hardware architectures for the binary modular exponentiation：Sequential,，parallel，and systolic,，IEEE Trans.Circuits Syst.I.Reg.2006,，53(3)：627–633.