0 引言

    公鑰密碼體制因其強大的安全性，廣泛應(yīng)用于信息安全領(lǐng)域,。橢圓曲線密碼算法與RSA相比,，具有相同安全性下運算速度更快、占用資源更少,、位寬更低的優(yōu)點,，成為新一代的公鑰密碼體制標準。橢圓曲線密碼處理器通常根據(jù)每秒鐘點乘的計算次數(shù)作為衡量其性能好壞的標準之一,。實現(xiàn)點乘運算,，要大量調(diào)用模乘、模除和模加減等有限域?qū)幽＿\算,。模除運算最為復雜,，耗時最多，通常引入投影坐標系,，降低調(diào)用次數(shù),。而與模乘相比，模加減的運算量幾乎可以忽略。模乘是橢圓曲線密碼算法中最基本,、最核心的一種模運算,，提高其運算速度將有效提高橢圓曲線密碼處理器性能。

    如今,，設(shè)計一種靈活高效,、適用于多種安全場景的模乘器仍然是研究熱點。文獻[1]基于CPA和CSA結(jié)構(gòu)實現(xiàn)了的統(tǒng)一的MALU單元,，能夠有效完成模運算,，資源復用率高，靈活性和可擴展性強,，但是隨著運算位寬的增加,，CPA的進位鏈會成為瓶頸，大大制約著電路的性能,。文獻[2]采用64位的基4 Kogge-Stone超前進位加法器實現(xiàn)DFA,，實現(xiàn)新型的Wallace數(shù)乘法單元，縮短了運算時間,，但硬件資源占用較多,。文獻[3]在Blakley算法的基礎(chǔ)上，提出改進的Radix-4快速模乘算法,，采用Booth編碼減少迭代次數(shù),，并采用符號估計技術(shù)避免大整數(shù)比較，還基于擴展Euclidean求逆算法,，設(shè)計統(tǒng)一硬件電路,，雖然面積很小，但是運算速度不高,。本文根據(jù)基于Radix-4交錯模乘算法^[4],，采用進位保留加法器(Carry Save Adder，)和Kogge-Stone加法器(Kogge-Stone Adder,，KSA)^[5]組合的加法結(jié)構(gòu),，縮短電路關(guān)鍵路徑，同時支持素數(shù)域GF(p)和二元域GF(2^m)的模乘運算,。根據(jù)操作數(shù)位寬控制迭代輪數(shù),，靈活適配各種長度的模乘運算。

1 背景介紹

1.1 Kogge-Stone加法器

    在硬件電路設(shè)計中,，基礎(chǔ)的加減乘除運算,，最終都可以通過多次加法計算來實現(xiàn)，因此加法器是許多運算模塊的基礎(chǔ)單元,，其性能好壞直接關(guān)系到整個電路的性能,。對于傳統(tǒng)加法器，如串行進位加法器、進位選擇加法器,，高位的計算需要低位的進位輸出,。隨著運算位寬的增加，加法器的進位鏈不斷增長,，大大制約著加法器的運算性能,。為了減少進位時間，1973年,，KOGGE P M和STONE H S提出了并行前綴的超前進位加法器,，使高位的計算與前一位的進位結(jié)果無關(guān)，從而大大提高加法器的速度,。

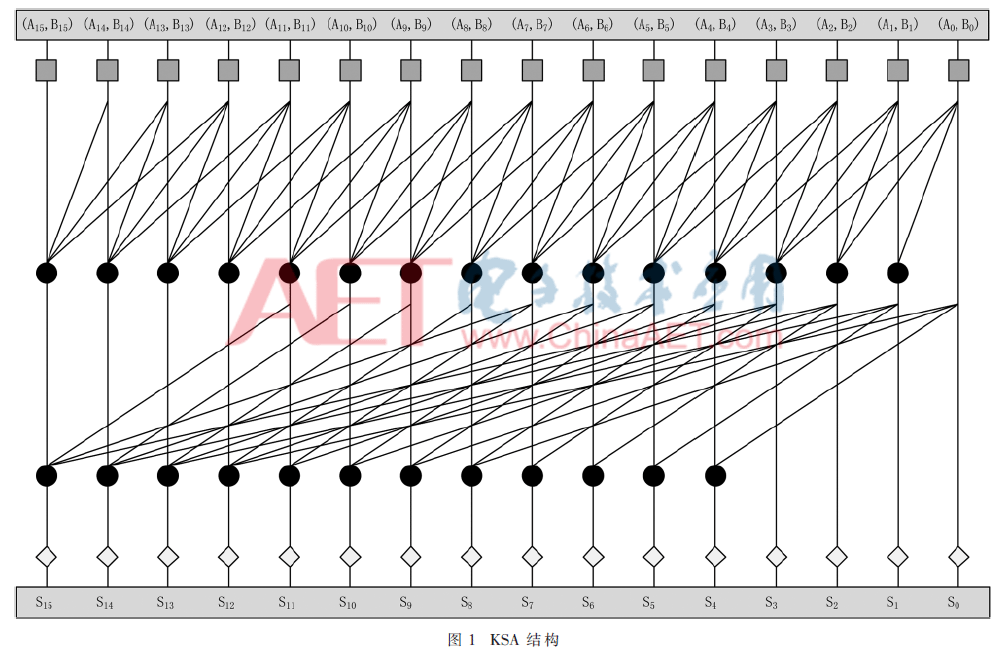
    本文中KSA采用4位一組的點操作,，計算延遲是log₄N級點操作的延遲，與普通的二進制KSA加法器結(jié)構(gòu)相比速度提高一倍,。圖1是以計算16位加法為例的四進制KSA結(jié)構(gòu)^[4],，該結(jié)構(gòu)由三種基本單元構(gòu)成,。最上面的正方型代表前置進位信號產(chǎn)生電路,，用于產(chǎn)生進位傳播信號P_i和進位產(chǎn)生信號G_i。最下面的菱形表示最終的進位生成電路與求和電路,，用于產(chǎn)生每一位的進位信號C_i與加法和S_i,。中間的圓形代表Kogge-Stone樹結(jié)構(gòu)，用于產(chǎn)生進位信號C_i所需的中間結(jié)果,，包括塊進位產(chǎn)生信號和塊進位傳播信號,。

1.2 進位保留加法器

    進位保留加法器(CSA)常用于多操作數(shù)的加法。假設(shè)計算三個m比特的操作數(shù)A,、B和C的和,，采用CSA結(jié)構(gòu)，將輸出兩個結(jié)果：本位異或結(jié)果sum與進位carry,。還需要一個加法器將sum和carry相加,，本文中，CSA和KSA共同完成三操作數(shù)相加,。

    CSA用表達式可以表示為：

1.3 模乘算法分析

    模乘是橢圓曲線密碼的核心運算,，本文中交錯模乘算法如算法1所示，支持素數(shù)域GF(p)和二元域GF(2^m)上的運算,。

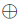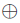    二元域運算與素數(shù)域的不同在于二元域運算沒有進位,，運算更加簡單。素數(shù)域中的模數(shù)P,，在二元域中表示為不可約多項式F(x),。模乘素數(shù)域用進行2Amod P、4Amod P和x+y+zmod P三種運算，在二元域中表示為x·A(x)mod F(x),、x2·A(x)mod F(x)和xyz,。

2 模乘結(jié)構(gòu)

2.1 模乘總體結(jié)構(gòu)

    根據(jù)Radix-4交錯模乘算法，本文設(shè)計了長度可變的雙域模乘器,，其總體結(jié)構(gòu)如圖2所示,。實線框內(nèi)表示素數(shù)域的模乘運算單元，長虛線框內(nèi)表示用于二元域模乘的運算單元,。短虛線框中標出的是本結(jié)構(gòu)中的復用部分,，一是x²·A(x)modf(x)結(jié)構(gòu)復用了x·A(x)modf(x)結(jié)構(gòu)；二是復用x+y+zmod P結(jié)構(gòu)中的CSA0中三操作數(shù)的異或輸出sum,，實現(xiàn)二元域上的三操作數(shù)相異或,。

    該結(jié)構(gòu)由運算單元、控制器和中間數(shù)據(jù)寄存器組成,。

    運算單元是雙域模乘器的核心部分,，主要包括2Amod P結(jié)構(gòu)、4Amod P結(jié)構(gòu),、x+y+zmod P結(jié)構(gòu),、x·A(x)mod f(x)結(jié)構(gòu)和x²·A(x)mod f(x)結(jié)構(gòu)。

    中間數(shù)據(jù)寄存器主要用于寄存每一輪迭代計算出的U,、V,、A、B的值,，數(shù)據(jù)選擇器選擇寄存運算單元的結(jié)果,。

    控制器基于狀態(tài)機設(shè)計，產(chǎn)生數(shù)據(jù)路徑中數(shù)選器的選擇信號,，以控制數(shù)據(jù)路徑中的數(shù)據(jù)流向,，完成雙域模乘運算時各個模塊的調(diào)度控制。并根據(jù)域選擇信號以及數(shù)據(jù)長度,，進行判斷執(zhí)行素數(shù)域還是二元域運算,，以及迭代輪數(shù)。

2.2 雙域模乘器運算單元

2.2.1 素數(shù)域

    （1）2Amod P結(jié)構(gòu)

    實現(xiàn)2Amod P,，即完成A左移一位,，再判斷2A與P的大小決定是否進行“-P”操作，以實現(xiàn)0≤2Amod P<P,。由于0≤A<P,，則0≤2A<2P，故2Amod P的結(jié)果分兩種情況：

    2Amod P結(jié)構(gòu)如圖3所示,，該結(jié)構(gòu)由一個KSA和一個數(shù)據(jù)選擇器組成,。KSA主要用來計算2A-P,，數(shù)據(jù)選擇器將KSA的進位輸出作為數(shù)選信號，判斷2Amod P的輸出結(jié)果,。

    (2)4Amod P結(jié)構(gòu)

    實現(xiàn)4Amod P,，首先A左移兩位，再判斷4A與P的大小,，重復進行“-P”操作直至0≤4Amod P<P,。由于0≤A<P，則0≤4A<4P,，故4Amod P的結(jié)果分四種情況：

    4Amod P結(jié)構(gòu)如圖4所示,，該結(jié)構(gòu)由1個CSA和3個KSA組成。并行計算4A-P,、4A-2P,、4A-3P，根據(jù)三個KSA的進位輸出作為數(shù)選信號,，選擇最后輸出結(jié)果,。

    (3)x+y+zmod P結(jié)構(gòu)

    實現(xiàn)x+y+zmod P，先計算x+y+z,，再判斷x+y+z與P的大小,，重復進行“-P”操作直至0≤x+y+zmod P<P。由于0≤x,、y,、z<P,，則0≤x+y+z<3P,，故x+y+zmod P的結(jié)果分三種情況：

    x+y+zmod P結(jié)構(gòu)如圖5所示，該結(jié)構(gòu)由3個CSA和3個KSA組成,。并行計算x+y+z,、x+y+z-P、x+y+z-2P,，根據(jù)KSA1和KSA2的進位輸出作為數(shù)選信號,，選擇最后輸出結(jié)果。

2.2.2 二元域

    二元域不同于素數(shù)域,，算法更為簡單,，移位與異或即可實現(xiàn)x乘，將操作數(shù)按位異或即可實現(xiàn)加法,，無需考慮進位,。

    (1)加法結(jié)構(gòu)

    本文中，二元域三操作數(shù)異或通過復用x+y+zmod P結(jié)構(gòu)中的CSA0實現(xiàn),。

    (2)x乘結(jié)構(gòu)

    實現(xiàn)x·A(x)mod f(x),，即將A(x)左移一位,，如果a_m-1=1，將之與f(x)進行異或,。

    其結(jié)構(gòu)如圖6所示,，將此結(jié)構(gòu)進行級聯(lián)，即可實現(xiàn),。

3 性能分析

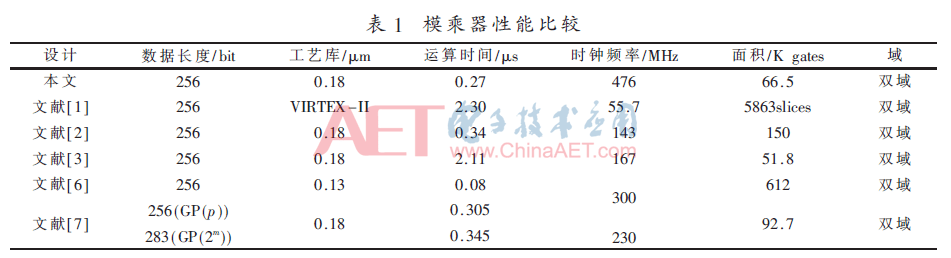
    本文采用Verilog HDL硬件描述語言對雙域模乘器進行RTL級描述,，并利用ModelSim進行功能仿真驗證。在0.18 μm CMOS工藝標準單元庫對雙域模乘器進行邏輯綜合,，綜合工具使用Synopsys公司的Design Complier,。綜合結(jié)果表明，雙域模乘器占用硬件資源66 518 gates,，最高時鐘可達到476 MHz,，計算256 bit的模乘運算僅需0.27 μs。

    本文中雙域模乘器結(jié)構(gòu)的關(guān)鍵路徑在于CSA和KSA組合的加法結(jié)構(gòu),。為了驗證模乘器的性能,，將本文和其他文獻的模乘單元的性能進行比較，其結(jié)果如表1所示,。本文與文獻[2]相比,，模乘運算時間降低了20.59%，且面積減小了55.67%,。本文的運算時間是文獻[6]的3.38倍,，但面積大概只有文獻[6]的1/10。與文獻[3]相比,，雖然面積略大,，但256 bit的計算時間降低了87.2%。與文獻[7]相比,，本文速度降低不多,，但面積減小了28.26%。綜上,，本文的雙域模乘器在速度和面積上具有綜合優(yōu)勢,。

    綜合比較，本設(shè)計能同時支持素數(shù)域GP(p)和二元域GP(2^m)的模乘運算,，并且適配不同長度的位寬需求,，具有較強的靈活性和可擴展性。

4 結(jié)論

    本文基于雙域Radix-4交錯模乘算法,，采用CSA和KSA組合的加法結(jié)構(gòu),，實現(xiàn)長度可伸縮的雙域模乘器。采用基于Kogge-Stone結(jié)構(gòu)的并行前綴加法器,，減小了進位延遲,，縮短了該模乘單元的關(guān)鍵路徑,，大大提高了運算頻率，尤其當運算位寬越大,，優(yōu)勢越明顯時,。結(jié)構(gòu)上復用了素數(shù)域x+y+zmod P結(jié)構(gòu)的CSA0加法器中的異或門實現(xiàn)二元域中的三操作數(shù)的異或，減少硬件資源,，提高單元利用率,。

參考文獻

[1] LIU Z，LIU D,，ZOU X.An efficient and flexible hardware implementation of the dual-field Elliptic curve cryptographic processor[J].IEEE Transactions on Industrial Electronics,，2017，64(3)：2353-2362.

[2] 郭曉,，蔣安平,，宗宇.SM2高速雙域Montgomery模乘的硬件設(shè)計[J].微電子學與計算機，2013(9)：17-21.

[3] 陳光化,，朱景明,，劉名，等.雙有限域模乘和模逆算法及其硬件實現(xiàn)[J].電子與信息學報,，2010,，32(9)：2095-2100.

[4] 李泉龍.基于Kogge-Stone算法與多米諾邏輯的64位高性能加法電路設(shè)計[D].成都：西南交通大學，2016.

[5] KOGGE P M,，STONE H S.A parallel algorithm for the efficient solution of a general class of recurrence Equations[J].IEEE Transactions on Computers,，1973，C-22(8)：786-793.

[6] 廖望,，萬美琳,，戴葵，等.可擴展雙域模乘器設(shè)計與研究[J].華中科技大學學報(自然科學版),，2015(9)：51-54.

[7] 李嘉敏,，戴紫彬,，王益?zhèn)?可編程可伸縮的雙域模乘加器研究與設(shè)計[J].電子技術(shù)應(yīng)用,，2018，44(1)：28-32,，36.

作者信息:

楊丹陽1,，楊  萱2，陳  韜1,，戴紫彬1,，李  偉1

(1.信息工程大學，河南 鄭州450001,；2．江南計算技術(shù)研究所,，江蘇 無錫214083)