0 引言

    管道泄漏不僅污染環(huán)境、影響生產(chǎn),，還會(huì)造成人員傷亡等,，因此對(duì)管道泄漏的檢測(cè)尤為重要^[1]。在眾多檢測(cè)方法中,，負(fù)壓波法因其原理簡(jiǎn)單,、定位準(zhǔn)確等優(yōu)點(diǎn)得到廣泛應(yīng)用。在管道泄漏檢測(cè)中,，管道周邊車輛行駛的噪聲,、管道上各種工況操作引起的噪聲等，都會(huì)造成負(fù)壓波信號(hào)信噪比較低,。管道泄漏的檢測(cè)和定位精度主要取決于負(fù)壓波信號(hào)的去噪效果和時(shí)延估計(jì)性能^[2],。

    針對(duì)管道泄漏信號(hào)處理，國(guó)內(nèi)外做了很多研究,。2014年,，席旭剛等^[3]提出一種基于噪聲統(tǒng)計(jì)特性的經(jīng)驗(yàn)?zāi)B(tài)分解(Empirical Mode Decomposition,，EMD)自相關(guān)去噪方法，能對(duì)低信噪比信號(hào)有效消噪,。2015年,，孫潔娣等^[4]利用總體局域均值分解和K-L散度原則進(jìn)行去噪；利用高階模糊度函數(shù)獲取信號(hào)特征頻率,，以完成定位,。2016年，Guo Chengcheng等^[5]將一端泄漏信號(hào)作為參考,，以另一端泄漏信號(hào)經(jīng)EMD分解后固有模態(tài)函數(shù)(Intrinsic Mode Function,，IMF)與參考信號(hào)的互相關(guān)值作為有效分量選取準(zhǔn)則，獲取有效IMF分量并重構(gòu)去噪,。

    文獻(xiàn)[4-5]在一定程度上提高了信號(hào)去噪效果和定位精度,，但對(duì)低信噪比信號(hào)的去噪、定位能力不足,。文獻(xiàn)[3]能用于低信噪比信號(hào)去噪,，但只對(duì)IMF1進(jìn)行噪聲統(tǒng)計(jì)特性去噪，缺少相關(guān)準(zhǔn)則準(zhǔn)確選取高頻含噪分量,。針對(duì)以上方法的局限性,，本文提出非局部均值（Non-Local Means，NLM）-EMD自相關(guān)去噪算法和模糊C均值聚類（Fuzzy C-Means clustering,，F(xiàn)CM）-二次相關(guān)自適應(yīng)時(shí)延估計(jì)算法,。在去噪方面，將基于結(jié)構(gòu)塊運(yùn)算的圖像NLM算法用于管道泄漏信號(hào)處理,，避免高頻IMF分量選取問題,，利用NLM進(jìn)行去噪預(yù)處理，彌補(bǔ)EMD對(duì)低信噪比信號(hào)去噪效果不理想的問題,。在時(shí)延估計(jì)方面，對(duì)去噪信號(hào)進(jìn)行FCM模糊聚類,，自適應(yīng)提取壓力下降段信號(hào),，突出泄漏特征，使二次相關(guān)峰值更加突出,，從而有效提高定位精度,。

1 NLM-EMD自相關(guān)去噪算法及仿真

1.1 NLM算法

    如圖1所示，對(duì)x(t)的去噪,，是在整個(gè)搜索區(qū)域M(s)=[s-K,，s+K]內(nèi)找到所有相似塊Δ_t(i)的加權(quán)平均^[6-7]，即：

1.2 NLM與EMD自相關(guān)組合去噪

    對(duì)于低信噪比信號(hào),，文獻(xiàn)[8]對(duì)EMD分解的高階IMF分量進(jìn)行離散小波變換,，以實(shí)現(xiàn)有效去噪,。但EMD和小波是針對(duì)信號(hào)鄰域內(nèi)點(diǎn)的處理或?qū)π盘?hào)本身數(shù)學(xué)函數(shù)的研究，對(duì)具有典型特征的信號(hào)結(jié)構(gòu)塊有所忽視,，影響去噪效果,。

    針對(duì)該問題，本文提出基于結(jié)構(gòu)塊的NLM-EMD自相關(guān)去噪算法,。利用NLM進(jìn)行去噪預(yù)處理,，提高EMD分解質(zhì)量。根據(jù)EMD自相關(guān)準(zhǔn)則,，求取IMF分量歸一化自相關(guān)函數(shù)及方差,，選取方差大于閾值的分量重構(gòu)。

1.3 仿真實(shí)驗(yàn)

    理想狀態(tài)下管道發(fā)生泄漏時(shí),，管道內(nèi)產(chǎn)生瞬態(tài)壓力變化,，傳感器采集的信號(hào)類似于斜坡信號(hào)。由于環(huán)境噪聲干擾,，用awgn函數(shù)添加一定信噪比高斯白噪聲模擬實(shí)際泄漏信號(hào),，如圖2所示。

    由圖2可知,，泄漏信號(hào)中含大量噪聲,，信號(hào)規(guī)律不明顯。進(jìn)行NLM預(yù)處理,，目標(biāo)塊半寬度p=10,，搜索區(qū)域?yàn)檎麄€(gè)區(qū)域，濾波器參數(shù)λ=0.1,。結(jié)果如圖3所示,，信噪比由8 dB提高至20.153 4 dB，噪聲得到有效抑制,。

    對(duì)NLM降噪后的信號(hào)進(jìn)行EMD分解,，得到9階IMF分量和1個(gè)殘余分量。計(jì)算各階分量的歸一化自相關(guān)函數(shù)及方差：0.000 5,、0.001 2,、0.002 2、0.005,、0.008 5,、0.017 5、0.071 9,、0.136 2,、0.192 4、0.083 3。選取方差大于閾值0.01的IMF6~10重構(gòu),，得到圖4,，信噪比提高至32.295 dB，有效去除了噪聲,，真實(shí)還原出原始信號(hào),。

2 FCM-二次相關(guān)自適應(yīng)時(shí)延估計(jì)算法

2.1 FCM算法

    FCM算法采用信號(hào)點(diǎn)樣本X={x₁，x₂,，…,，x_n}到每個(gè)聚類中心v_i(1≤i≤c)的加權(quán)距離平方和作為目標(biāo)函數(shù)^[9]：

式中，n為信號(hào)點(diǎn)樣本數(shù),；c(1<c<n)為聚類中心個(gè)數(shù),；m為模糊加權(quán)指數(shù)；u_ij,、d_ij分別為信號(hào)點(diǎn)樣本x_j到聚類中心v_i的隸屬度和歐式距離,；U=[u_ij]_c×n為模糊分類矩陣；V=[v₁,，v₂,，…，v_n]為聚類中心向量,。

    FCM的實(shí)質(zhì)是求解目標(biāo)函數(shù)的極小值,，通過迭代不斷修正模糊分類矩陣U和聚類中心V，使其滿足迭代精度,。

2.2 FCM與二次相關(guān)組合時(shí)延估計(jì)

    針對(duì)二次相關(guān)法時(shí)延估計(jì)精度有待提高的問題,，本文利用FCM自適應(yīng)提取相關(guān)性較高的壓力下降段信號(hào)，突出泄漏特征,，然后對(duì)其進(jìn)行二次相關(guān),，可以有效銳化二次相關(guān)峰值，以實(shí)現(xiàn)高精度時(shí)延估計(jì),。具體步驟如下：

    (1)設(shè)置模糊加權(quán)指數(shù)m=3,；聚類中心個(gè)數(shù)c=3，分別表示幅值較大的壓力平穩(wěn)段,、幅值發(fā)生較大變化的壓力下降段以及幅值較小的壓力平穩(wěn)段,。

    (2)將入口去噪信號(hào)作為信號(hào)點(diǎn)樣本X={x₁，x₂,，…，x_n},，用信號(hào)點(diǎn)所處的位置和信號(hào)點(diǎn)的值作為特征向量,。

    (3)利用FCM處理樣本特征向量，得到最終模糊分類矩陣U,。根據(jù)最大隸屬度原則,，提取壓力下降聚類中心的信號(hào)點(diǎn)樣本并重構(gòu),，得到壓力下降段信號(hào)。

    (4)對(duì)出口去噪信號(hào),，進(jìn)行步驟(1)~(3),，得到出口壓力下降段信號(hào)。根據(jù)這兩段信號(hào)的壓力下降開始點(diǎn)x(t_start1),、x(t_start2)和壓力下降結(jié)束點(diǎn)x(t_end1),、x(t_end2)，分別在入口,、出口去噪信號(hào)上截取min(x(t_start1),，x(t_start2))至max(x(t_end1)，x(t_end2))段作為壓力下降段,。

    (5)對(duì)兩段壓力下降段信號(hào)進(jìn)行二次相關(guān)得時(shí)延值,。

3 管道泄漏定位實(shí)驗(yàn)

3.1 管道泄漏定位流程

    管道發(fā)生泄漏時(shí)，在泄漏點(diǎn)內(nèi)外壓差作用下產(chǎn)生瞬態(tài)壓力變化,，形成負(fù)壓波,，并向管道兩端傳播。入口,、出口傳感器的距離為L(zhǎng),，則泄漏點(diǎn)距離入口傳感器的距離為[10]：

式中，v為負(fù)壓波速度,，Δt=t₂-t₁為負(fù)壓波到達(dá)2個(gè)傳感器的時(shí)間差,。

    針對(duì)EMD對(duì)低信噪比信號(hào)去噪效果不理想及二次相關(guān)時(shí)延估計(jì)精度有待提高問題，本文利用NLM-EMD自相關(guān)去噪,，然后進(jìn)行FCM-二次相關(guān)自適應(yīng)時(shí)延估計(jì),，結(jié)合負(fù)壓波速度進(jìn)行泄漏定位。整個(gè)管道泄漏定位流程如圖5所示,。

3.2 實(shí)驗(yàn)系統(tǒng)搭建

    搭建如圖6所示的實(shí)驗(yàn)管道系統(tǒng),。蛇形管道長(zhǎng)113 m、內(nèi)徑40 mm,；2只壓力變送器,，間距93 m；3個(gè)泄漏閥門,，距離入口壓力變送器分別為5.4 m,、21.4 m和69.4 m；NI PXI-446 1動(dòng)態(tài)信號(hào)分析儀,，采樣頻率為500 Hz,；負(fù)壓波速度為1 120 m/s。

3.3 實(shí)驗(yàn)信號(hào)處理

    圖7為1號(hào)泄漏閥門打開時(shí)入口壓力變送器采集的泄漏信號(hào)。受環(huán)境噪聲干擾,，泄漏信號(hào)信噪比較低,。

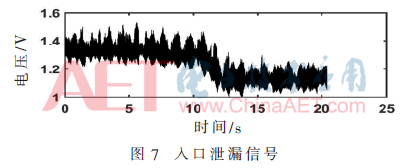
    利用NLM對(duì)泄漏信號(hào)進(jìn)行預(yù)處理。設(shè)置目標(biāo)塊半寬度p=10,，搜索區(qū)域?yàn)檎麄€(gè)區(qū)域,，濾波器參數(shù)λ=0.1。結(jié)果如圖8（a）所示,，可以看出隨機(jī)噪聲得到很好的抑制,，信噪比明顯改善。

    對(duì)經(jīng)NLM預(yù)處理后的信號(hào)進(jìn)行EMD分解,，得到11階IMF分量,。計(jì)算IMF分量的歸一化自相關(guān)函數(shù)及方差，分別為0.030 9,、0.006 5,、0.001 6、0.001 7,、0.004 9,、0.015 9、0.036 5,、0.039 5,、0.105、0.204 3,、0.083 3,。設(shè)定閾值為0.035，選取方差大于閾值的IMF7~11進(jìn)行重構(gòu),，如圖8（b）所示,。原始信號(hào)經(jīng)NLM-EMD自相關(guān)去噪后，噪聲被明顯去除,，真實(shí)還原了有效信號(hào),，同時(shí)特征信息豐富，有力地證明了NLM-EMD自相關(guān)法的優(yōu)越性,。

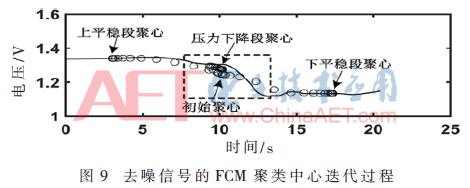
    利用FCM處理去噪后的信號(hào),，其中模糊加權(quán)指數(shù)m=3；聚類中心個(gè)數(shù)c=3,；迭代精度ε=0.001,，最大迭代次數(shù)為500。結(jié)果如圖9所示,，其中小圓圈代表聚類中心迭代修正過程,，所有信號(hào)分布在3個(gè)聚類中心(3.027 3,，1.338 7)、(10.209 2,，1.273 6)、(17.392 5,，1.132)附近,。根據(jù)最大隸屬度原則，圖9中7.494~12.918 s對(duì)應(yīng)的信號(hào)點(diǎn)屬于壓力下降聚類,，如圖中虛線框所示,。

    對(duì)出口泄漏信號(hào)進(jìn)行NLM-EMD自相關(guān)及FCM模糊聚類，得到出口壓力下降段信號(hào),，為7.496~12.922 s對(duì)應(yīng)的信號(hào),。選取入口、出口2個(gè)壓力下降開始點(diǎn)對(duì)應(yīng)時(shí)間的最小值7.494 s和2個(gè)壓力下降結(jié)束點(diǎn)對(duì)應(yīng)時(shí)間的最大值12.922 s進(jìn)行壓力下降段截取,，如圖10所示,。入口、出口壓力下降段被精確提取出來,，上,、下平穩(wěn)段信號(hào)的噪聲干擾被自適應(yīng)去除，兩信號(hào)間有一定偏移,，對(duì)應(yīng)時(shí)間延遲,。

    對(duì)入口、出口壓力下降段信號(hào)進(jìn)行二次相關(guān),。根據(jù)互相關(guān)峰值得到時(shí)延為73 ms,，帶入式（3）可得定位位置為5.62 m，相對(duì)定位誤差為(5.62-5.4)/93=0.24%,。

3.4 算法驗(yàn)證

    為了進(jìn)一步說明本文算法用于管道泄漏定位的優(yōu)越性,，在1、2,、3號(hào)泄漏閥門處分別進(jìn)行3次泄漏實(shí)驗(yàn),，同時(shí)分別用NLM-EMD自相關(guān)去噪+FCM-二次相關(guān)法、小波閾值去噪+FCM-二次相關(guān)法,、NLM-EMD自相關(guān)去噪+二次相關(guān)法對(duì)9組泄漏信號(hào)進(jìn)行泄漏定位,，結(jié)果如表1所示。

    由表1可知,，NLM-EMD自相關(guān)去噪+FCM-二次相關(guān)法的平均定位誤差為0.69 m,，遠(yuǎn)小于小波去噪法的4.19 m和二次相關(guān)法的1.45 m。與小波去噪相比,，NLM-EMD自相關(guān)法能更加有效去除低信噪比信號(hào)的噪聲,，同時(shí)保留泄漏信號(hào)的大部分特征信息,。與二次相關(guān)法相比，F(xiàn)CM-二次相關(guān)法能進(jìn)行自適應(yīng)截取,，突出相關(guān)性較高的壓力下降段信號(hào),，銳化二次相關(guān)峰值，使定位誤差更小,。

4 結(jié)論

    針對(duì)管道泄漏定位精度差的問題,，本文提出NLM-EMD自相關(guān)去噪算法和FCM-二次相關(guān)自適應(yīng)時(shí)延估計(jì)算法。

    (1)利用NLM對(duì)泄漏信號(hào)進(jìn)行降噪預(yù)處理,，仿真實(shí)驗(yàn)表明泄漏信號(hào)信噪比由8 dB提高到20.153 4 dB,；然后進(jìn)行EMD自相關(guān)去噪，信噪比最終提高到32.295 dB,。本文去噪算法能改善EMD分解質(zhì)量,，有效去除噪聲干擾。

    (2)利用FCM自適應(yīng)提取相關(guān)性較強(qiáng)的壓力下降段信號(hào),，可以增強(qiáng)兩泄漏信號(hào)的相關(guān)性,，提高二次相關(guān)時(shí)延估計(jì)精度，實(shí)驗(yàn)信號(hào)相對(duì)定位誤差僅為0.24%,。通過與直接二次相關(guān)法比較,，本文算法的定位精度提高了0.817%。

    本文算法能對(duì)管道泄漏信號(hào)進(jìn)行有效去噪,，且定位精度高,，為管道泄漏檢測(cè)提供了一種新思路。

參考文獻(xiàn)

[1] 陳世利,，譚皓予,，李健，等.一種基于ARM-Linux的分布式管道泄漏監(jiān)測(cè)系統(tǒng)[J].電子技術(shù)應(yīng)用,，2011,，37(10)：73-76.

[2] GAO Y，BRENNAN M J,，JOSEPH P F.On the effects of reflections on time delay estimation for leak detection in buried plastic water pipes[J].Journal of Sound & Vibration,，2009，325(3)：649-663.

[3] 席旭剛,，武昊,，羅志增.基于EMD自相關(guān)的表面肌電信號(hào)消噪方法[J].儀器儀表學(xué)報(bào)，2014,，35(11)：2494-2500.

[4] 孫潔娣,，肖啟陽，溫江濤,，等.改進(jìn)LMD及高階模糊度函數(shù)的管道泄漏定位[J].儀器儀表學(xué)報(bào),，2015,，36(10)：2215-2223.

[5] Guo Chengcheng，Wen Yumei,，Li Ping,，et al.Adaptive noise cancellation based on EMD in water-supply pipeline leak detection[J].Measurement，2016,，79：188-197.

[6] 趙慶平,，陳得寶，姜恩華,，等.一種改進(jìn)權(quán)重的非局部均值圖像去噪算法[J].電子測(cè)量與儀器學(xué)報(bào)，2014,，28(3)：334-339.

[7] 祝青林,，呂勇，李寧.非局部均值去噪和LMD綜合的滾動(dòng)軸承故障診斷[J].機(jī)床與液壓,，2015,，43(13)：172-176.

[8] KABIR M A，SHAHNAZ C.Denoising of ECG signals based on noise reduction algorithms in EMD and wavelet domains[J].Biomedical Signal Processing & Control,，2012,，7(5)：481-489.

[9] 張淑清，孫國(guó)秀,，李亮,，等.基于LMD近似熵和FCM聚類的機(jī)械故障診斷研究[J].儀器儀表學(xué)報(bào)，2013,，34(3)：714-720.

[10] ADNAN N F,，GHAZALI M F，AMIN M M,，et al.Leak detection in gas pipeline using Hilbert-Huang transform[J].Applied Mechanics & Materials,，2015，815(1)：403-407.