0 引言

    盲源分離(Blind Source Separation，BSS)^[1]技術(shù)旨在從M個混合信號中恢復(fù)出N個統(tǒng)計獨立的源信號,，這里的“盲”是指源信號和混合信道的先驗知識未知,。由于這種“盲”的特性，BSS被廣泛的應(yīng)用于數(shù)字通信,、陣列信號處理、語音和圖像處理等領(lǐng)域中,。線性瞬時混合模型是BSS問題中最常見的模型之一,，適用于遠(yuǎn)程通信等環(huán)境，該模型同時也是其他混合模型(如卷積混合)的基礎(chǔ)模型,，其數(shù)學(xué)描述如下：

其中A為未知混合矩陣,，t為采樣時刻，s(t)=[s₁(t),，…,，s_N(t)]^T為N個未知的統(tǒng)計獨立的源信號組成的矢量，x(t)=[x₁(t),，…,，x_M(t)]^T由M個可獲取的混合信號組成，n(t)=[n₁(t),，…,，n_M(t)]^T包含M路加性高斯白噪聲。此時,，BSS問題轉(zhuǎn)化為尋找一個解混矩陣W,，使得輸出y(t)=Wx(t)為輸入s(t)的估計，且允許存在幅度和排列次序的不確定性,。

    為解決上述問題,，很多有效的方法被提出，如基于獨立成分分析^[2]、非線性主成分分析^[3]的方法等,，但是這些方法大部分都需要已知源信號的數(shù)目,，而且一般都假設(shè)源信號的數(shù)目與混合信號的數(shù)目相等，即M=N,。在實際應(yīng)用中,，這樣的設(shè)定往往是不成立的，因為源信號數(shù)目作為源端信息常常是不可直接獲取的,，甚至有可能動態(tài)變化,，例如在無線通信系統(tǒng)中，接入系統(tǒng)的用戶數(shù)目可能隨時都在改變,?？梢姡瑢嶋H應(yīng)用中,，M=N很難滿足,，當(dāng)設(shè)定接收混合信號的傳感器數(shù)目足夠多時，往往出現(xiàn)M>N的超定情況,。對于源數(shù)目未知且在超定假設(shè)下的BSS問題,，文獻(xiàn)[4]首先在白化階段估計出源數(shù)目，然后將混合信號維度M降低到,，利用自然梯度算法解決上述BSS問題,，但是當(dāng)混合矩陣為病態(tài)時或者源信號之間幅值比例失調(diào)嚴(yán)重時，這種算法可能會失效,。文獻(xiàn)[5]從理論上證明了最小互信息準(zhǔn)則能夠用在超定的情況下,，并提出一種適用于未知源數(shù)目的改進(jìn)的自然梯度算法。文獻(xiàn)[6]利用自組織結(jié)構(gòu)的神經(jīng)網(wǎng)絡(luò)對瞬時源信號數(shù)目進(jìn)行估計,，并調(diào)整神經(jīng)網(wǎng)絡(luò)大小進(jìn)行混合信號的分離,。文獻(xiàn)[7]提出一種自適應(yīng)神經(jīng)網(wǎng)絡(luò)算法(Adaptive Neural Algorithm, ANA)進(jìn)一步提高了收斂的穩(wěn)定性，但是收斂速度較慢,。文獻(xiàn)[8]在ANA算法的基礎(chǔ)上加入了動量項,，提出了一種基于神經(jīng)網(wǎng)絡(luò)和動量項的動態(tài)源恢復(fù)算法(Neual Network with Momentum for Dynamic Source Number，NNM-DSN),，該算法收斂速度更快且穩(wěn)態(tài)誤差更小,。但是上述算法通常都不考慮噪聲，算法的實用化程度不高,。

    本文針對含噪動態(tài)源條件下的BSS問題,，提出了一種新型在線盲源分離算法，該算法包括兩部分：第一部分是基于最小描述長度(Rissanen’s Minimum Description Length,，MDL)^[9]的一種動態(tài)源數(shù)目估計算法,，該算法能實時精確地估計信道中的瞬時信源數(shù)目,；第二部分是基于偏差去除的變步長神經(jīng)網(wǎng)絡(luò)算法，該算法采用前饋神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu),，在學(xué)習(xí)準(zhǔn)則中加入了由噪聲引起的偏差去除項,，并在此基礎(chǔ)上給出了變步長策略。仿真實驗表明,，本文算法在含噪靜態(tài)源和動態(tài)源情況下能實現(xiàn)源信號的準(zhǔn)確恢復(fù),，相比于含噪情況下的ANA算法以及NNM-DSN算法，本文算法在靜態(tài)源和動態(tài)源情況下性能都更加優(yōu)異,，收斂速度更快,，且穩(wěn)態(tài)分離性能接近無噪情況下NNM-DSN算法的性能。

1 算法介紹

    對于含噪動態(tài)源條件下的BSS問題,，首先必須要確定瞬時源信號數(shù)目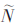,，然后將混合信號矢量的維度降低到維，其中M-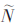個高度相關(guān)的成分將被去除,，以此來調(diào)整神經(jīng)網(wǎng)絡(luò)的大小,，使得問題變成源信號數(shù)目和混合信號數(shù)目相等的含噪BSS問題，利用本文提出的基于偏差去除的變步長神經(jīng)網(wǎng)絡(luò)算法即可得到源信號的估計,。圖1所示為算法的框架圖,，其中神經(jīng)網(wǎng)絡(luò)和學(xué)習(xí)算法共同作用可實現(xiàn)混合信號的分離。下面將分別介紹源數(shù)目估計和混合信號分離方法,。

1.1 源數(shù)目估計

    對于動態(tài)源的瞬時源數(shù)目估計,，文獻(xiàn)[7]采用改進(jìn)的交叉驗證(cross-validation)算法；文獻(xiàn)[8]對混合信號協(xié)方差進(jìn)行特征分解,，利用特征值的結(jié)構(gòu)對源信號數(shù)目進(jìn)行估計，但是上述算法均用于無噪聲的條件下,。一些經(jīng)典的批處理源數(shù)目估計算法（如MDL）可以用在有噪聲的情況下,，因此本文基于MDL提出一種動態(tài)源數(shù)目估計算法，能實時精確地估計信道中的信源數(shù)目,。

    選用當(dāng)前時刻和前B-1時刻的混合信號值對當(dāng)前時刻的源信號數(shù)目進(jìn)行估計,，定義t時刻的瞬時協(xié)方差矩陣為：

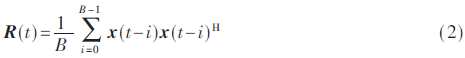
其中，上標(biāo)H代表共軛轉(zhuǎn)置操作,，t≥B,。當(dāng)t<B時，瞬時協(xié)方差矩陣按文獻(xiàn)[7]中給出的遞歸方式獲得,。對瞬時協(xié)方差矩陣進(jìn)行特征值分解得到M個特征值如下(降序排列)：

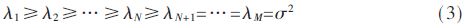
其中,，σ²為噪聲的功率，則利用MDL檢測準(zhǔn)則即可估計出當(dāng)前時刻的瞬時源信號數(shù)目,。

    利用上述方法進(jìn)行瞬時源信號數(shù)目估計存在一個問題,，即在源信號數(shù)目變化處,，會出現(xiàn)一小段過估計的情況。如圖2所示為源信號數(shù)目變化處的示意圖,，N₁為源信號數(shù)目變化前的信號個數(shù),，N₂為變化后的信號個數(shù)，t₁時刻為源信號數(shù)目變化的臨界點,，可以看出此時刻的前B-1個時刻處,，源信號數(shù)目保持穩(wěn)定不變，因此利用上述方法能準(zhǔn)確地估計出源信號數(shù)目為N₁,。t₂時刻滿足t₂-B+1=t₁,，且前B-1個時刻處，源信號數(shù)目保持穩(wěn)定,，因此同理可準(zhǔn)確估計出源信號數(shù)目為N₂,。在t₁和t₂之間的時刻如t′處，源信號數(shù)目可能會過估計,，但由于t₁和t₂的時間差小于B,，所以這種過估計的持續(xù)時間不會超過B。

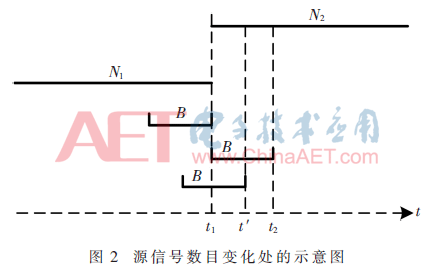
    為解決上述問題,，算法在檢測到源數(shù)目變化的時刻開始記錄當(dāng)前估計源數(shù)目值,，在此后的γB(1<γ≤1.5)時間內(nèi)，若估計源信號發(fā)生變化,，則將第一次變化與第二次變化之間的源數(shù)目值更改為第一次變化之前的源數(shù)目值,，再從第二次源數(shù)目變化的時刻開始記錄，重復(fù)上述的檢測,，直到在記錄開始時刻后的γB時間段內(nèi)估計源數(shù)目值不發(fā)生變化,，則停止記錄，等待下一次估計源數(shù)目變化,。采用這種方法即可消除源信號數(shù)目變換處的過估計問題,。

1.2 混合信號的分離

    一般地，解混矩陣的元素w_ij被認(rèn)為是神經(jīng)網(wǎng)絡(luò)的權(quán)值,，可以通過梯度下降法對其進(jìn)行調(diào)整,。本文考慮基于前饋神經(jīng)網(wǎng)絡(luò)的穩(wěn)健的學(xué)習(xí)準(zhǔn)則，表達(dá)式如下：

    將式(6)代入到式(4)中可得到基于偏差去除的神經(jīng)網(wǎng)絡(luò)算法,，但是算法中步長μ(t)必須適當(dāng)進(jìn)行選擇,，μ(t)太小則收斂速度過慢；反之,，則穩(wěn)態(tài)波動太大,。為克服上述問題，引入變步長策略,，參照文獻(xiàn)[11],，μ(t)可以按下列遞推式進(jìn)行調(diào)整：

2 仿真實驗

    為驗證本文提出算法在含噪動態(tài)源條件下的性能,，本文將與文獻(xiàn)[7]中的ANA算法和文獻(xiàn)[8]中的NNM-DSN算法進(jìn)行對比。源信號的選取與文獻(xiàn)[7-8]中一致,，設(shè)置采樣率為1 kHz,，則源信號波形示意圖如圖3所示，混合矩陣A隨機(jī)生成,，只要滿足列滿秩即可,。本文采用PI指數(shù)(performance index)^[2]來評價算法的分離性能，PI越小代表分離性能越好,。

    仿真實驗包括兩種情況,，一種是靜態(tài)源的情況，另一種是動態(tài)源的情況,。所有實驗將進(jìn)行100次Monte Carlo試驗,，在下面的實驗中，n=k(k≤6)的意思是取圖3中前k個信號作為源信號,，設(shè)置B=200,，γ=1.2。

2.1 靜態(tài)源的情況

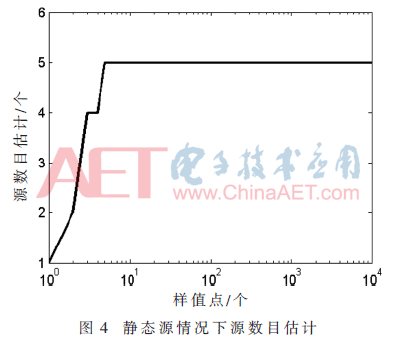
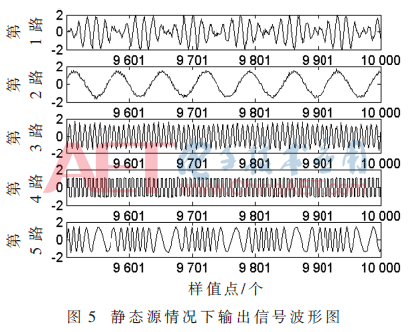
    本小節(jié)考慮靜態(tài)源的情況,，設(shè)n=5保持不變,，接收傳感器數(shù)為8，取10 000個樣值點,，信噪比(Signal-to-Noise Ratio,，SNR)設(shè)置為10 dB。圖4所示為靜態(tài)源情況下采用本文算法得到的源數(shù)目的估計圖,，可以看到算法很快得到了準(zhǔn)確的源數(shù)目,。圖5為靜態(tài)源情況下采用本文算法得到的輸出信號的波形圖，圖中顯示的是最后500個輸出樣值點,，由圖可知,，輸出信號完成了源信號的恢復(fù)，僅存在幅度和排列次序的不確定性,。圖6為有噪聲存在時ANA算法、NNM-DSN算法,、本文算法以及無噪聲時NNM-DSN算法在靜態(tài)源情況下的平均PI性能對比圖,，其中無噪聲時的NNM-DSN算法用來作性能參照，由圖可知,，當(dāng)噪聲存在時,，ANA算法和NNM-DSN算法性能惡化且穩(wěn)定性降低，而本文算法平均PI性能優(yōu)于含噪情況下的ANA算法和NNM-DSN算法,，且接近無噪聲時的NNM-DSN算法性能,，與含噪情況下的ANA算法和NNM-DSN算法相比,，本文算法也具有更快的收斂速度。

2.2 動態(tài)源的情況

    本小節(jié)考慮動態(tài)源的情況,，設(shè)n=3,，6，2,，取15 000個樣值點,，具體設(shè)置方式如下：

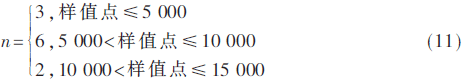
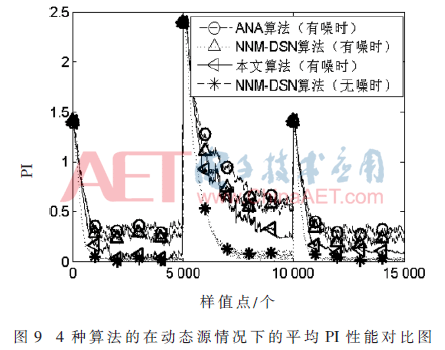
    設(shè)信噪比為10 dB，接收傳感器數(shù)為8,，圖7所示為動態(tài)源情況下本文算法進(jìn)行源數(shù)目估計的示意圖,，可以看到源數(shù)目得到了快速準(zhǔn)確的估計。圖8為動態(tài)源情況下采用本文算法得到的輸出信號波形圖,，取3種不同源數(shù)目情況下的分離信號最后300個樣值點,，其中空白框表示無輸出，由此可見,，混合信號被成功地分離,，僅存在幅度和排列次序的不確定性。圖9為有噪聲存在時ANA算法,、NNM-DSN算法,、本文算法以及無噪聲時NNM-DSN算法的在動態(tài)源情況下的平均PI性能對比圖，同樣,，無噪聲時的NNM-DSN算法用來作性能參照,，當(dāng)源數(shù)目動態(tài)變化時，所有算法都能調(diào)整至收斂,，ANA算法與NNM-DSN算法在有噪聲情況下平均PI定性變差,，與有噪聲情況下的ANA算法與NNM-DSN算法比較，本文算法平均PI性能更優(yōu),，收斂速度更快,，并且穩(wěn)態(tài)時的平均PI性能接近無噪聲時的NNM-DSN算法的性能,。

3 結(jié)論

    本文針對含噪動態(tài)源的情況提出了一種新型在線盲源分離算法,，包括兩部分,，即：基于MDL的動態(tài)源數(shù)目估計算法和基于偏差去除的變步長神經(jīng)網(wǎng)絡(luò)算法,。新型算法能實時準(zhǔn)確地估計出瞬時源信號的數(shù)目,，并在含噪條件下對混合信號進(jìn)行成功分離,。仿真實驗表明，本文算法在含噪靜態(tài)源和動態(tài)源情況下都能準(zhǔn)確地恢復(fù)出源信號,，相比于含噪情況下的ANA算法和NNM-DSN算法，本文算法具有更好的分離性能和更快的收斂速度,，且分離性能接近無噪情況下的NNM-DSN算法性能。

參考文獻(xiàn)

[1] COMON P,，CHRISTIAN J.Handbook of blind source separation：independent component analysis and applications[M].New York：Academic Press，2010.

[2] HYVARINEN A,，KARHUNEN J，OJA E.Independent component analysis[M].[S.l.]：John Wiley & Sons,，2001.

[3] KARHUNEN J,，JOUTSENSALO J.Representation and separation of signals using nonlinear PCA type learning[J].Neural Network,，1994,，7(1)：113-127.

[4] CICHOCKI A,，KARHUNEN J,，KASPRZAK W,，et al.Neural networks for blind separation with unknown number of sources[J].Neruocomputing,，1999，24(1-3)：55-93.

[5] YE J M,，ZHU X L，ZHANG X D.Adaptive blind source separation with an unknown number of sources[J].Neural computation,，2004，16(8)：1641-1460.

[6] SUN T Y,，LIU C C，HSIEH S T,，et al.Blind separation with unknown number of sources based on auto-trimmed neural network[J].Neurocomputing,，2008,，17(10-12)：2271-2280.

[7] SUN T Y，LIU C C,，TSAI S J,，et al.Blind source separation with dynamic source number using adaptive neural algorithm[J].Expert System With Application，2009,，36(5)：8855-8861.

[8] LI H,，SHEN Y，XUN K.Neural network with momentum for dynamic source separation and its convergence analysis[J].Journal of Networks,，2011,，6(5)：791-798.

[9] SCHWARZ G.Estimating the dimension of a model[J].Annu. Stat.，1987,，6(2)：461-464.

[10] DOUGLAS S C，CICHOCKI A,，AMARI S.A bias removal technique for blind source separation with noisy measurements[J].Electronics Letters,，1998,，34(14)：1379-1380.

[11] YUAN L，WANG W,，CHAMBERS J A.Variable step-size sign natural gradient algorithm for sequential blind source separation[J].IEEE Signal Processing Letters,，2005，12(8)：589-592.

[12] 趙偉,，沈越泓，王建功,，等.一種長時長混合通信信號的分離重建方法[J].軍事通信技術(shù),，2013，34(1)：62-68.