0 引言

    感應(yīng)式磁力儀基于法拉第電磁感應(yīng)原理,，用于探測近地空間的低頻交變磁場^[1],，它通常自帶標(biāo)準(zhǔn)信號源，用于在軌定標(biāo),。高質(zhì)量的定標(biāo)檢測信號,，是保證感應(yīng)式磁力儀探測到的變化磁場波形和頻譜信息科學(xué)性的前提。直接數(shù)字頻率合成技術(shù)^[2](Direct Digital Frequency Synthesis,，DDFS)于1971年被J.Tierney首次提出,。DDFS采用數(shù)字技術(shù)，以相位為出發(fā)點(diǎn)進(jìn)行頻率的合成,，具有高穩(wěn)定性,，高分辨率和較小的相位噪聲，DDFS的性能指標(biāo)遠(yuǎn)超傳統(tǒng)頻率合成技術(shù),，因此廣泛應(yīng)用于數(shù)字通信和精密儀器中,。利用直接數(shù)字頻率合成技術(shù)能為感應(yīng)式磁力儀提供高精度的標(biāo)準(zhǔn)定標(biāo)信號源。

    DDFS輸出信號的頻率表示為：

其中FCW為頻率控制字,，傳統(tǒng)方法的相幅映射結(jié)構(gòu)基于查找表ROM,。ROM容量隨輸出的位寬D成指數(shù)增長^[3]。為了減少ROM容量,，將相位累加器的位寬截斷并保留高W位,，作為相幅映射的輸入位寬。由于相位截斷,，會使合成信號的無雜散動態(tài)范圍(Spurious Free Dynamic Range,，SFDR)有明顯的下降。非量化輸出的SFDR為所截斷字長的線性函數(shù)^[4],，可近似為：

D為輸出信號的位寬,，SFDR應(yīng)大于量化信噪比。利用三角函數(shù)四分之一象限對稱性的象限壓縮方法,，能進(jìn)一步減少查找表容量,，節(jié)省75%的資源使用。

    僅依賴對相位字的截斷和象限壓縮,，無法可觀地減小查找表容量,。多種其他幅相映射方法被廣泛研究，通常分為兩大類：

    ROM壓縮算法的角分解法^[6]和ROM-Less的幅相轉(zhuǎn)換技術(shù),。ROM-Less型DDFS擺脫了大容量查找表的限制,，利用邏輯運(yùn)算,，將相位轉(zhuǎn)為幅度。如旋轉(zhuǎn)角算法(CORDIC算法)^[7],，泰勒級數(shù)展開算法^[8],，分段線性插值^[3]和分段多項式近似法^[9]。

    在分段多項式近似方法中,，隨分段多項式近似算法階數(shù)和分段數(shù)的增加,，在得到更小幅度誤差和高SFDR同時，增加了硬件資源占用和功率消耗,。因此平衡分段多項式近似算法的分段數(shù)與最高階,，是算法硬件實(shí)現(xiàn)平衡性能與資源占用的關(guān)鍵。

1 分段多項式近似算法方法研究

    用不等分的兩段四階偶次冪多項式近似為目標(biāo)函數(shù),，以區(qū)間壓縮方法為前提,，擬合余弦函數(shù)的前四分之一周期。相位分段點(diǎn)α將[0,，π/2]分為兩段,，擬合目標(biāo)函數(shù)表達(dá)式為：

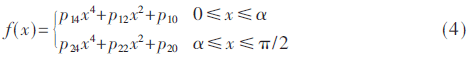
p_ij(i=1，2,，j=0,，2，4)表示為第i段,，j階的系數(shù)。最大幅度誤差MAE和SFDR是評價DDFS輸出信號的兩個重要指標(biāo),，MAE降低到0時,，理論上SFDR為無窮大。由于量化位寬和硬件資源的限制,，在實(shí)際的硬件電路中無法實(shí)現(xiàn),。可通過減小MAE來增大SFDR,。

    α值固定時,，通過最小均方MMSE得到對應(yīng)目標(biāo)函數(shù)最小誤差的多項式系數(shù)：

在相位點(diǎn)為α=π/3處，取得最MMSE,，最大絕對誤差為2.1×10^-4<2^-12,。表1為擬合結(jié)果多項式的系數(shù)。

    f(x)的SFDR理論上限可通過傅里葉級數(shù)展開獲得,，由于所合成的余弦信號為偶對稱信號,，且有四分之一象限的對稱性，因此只有奇數(shù)的余弦諧波系數(shù)非零,。

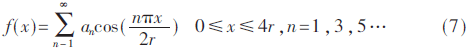
    圖1為式(4)算法的傅里葉變換頻譜圖,，圖中所示理論上的SFDR上限為94.98 dBc,。

    基于單段四階偶次冪多項式相幅映射輸出的SFDR理論上限為74.352 dBc^[9]。上述近似算法輸出信號的SFDR大于該上限超過20 dBc,。

2 基于定點(diǎn)數(shù)的相幅映射設(shè)計

    用霍納法則實(shí)現(xiàn)4階偶次多項式可減少一個乘法器使用,，降低運(yùn)算復(fù)雜度。

    本文所設(shè)計的DDFS結(jié)構(gòu)理論上SFDR最大值為94.98 dBc,，根據(jù)式(2)尋址位寬W應(yīng)有W>94.98,，取W=16，根據(jù)式(3)輸出D為15位,。上述DDFS結(jié)構(gòu)圖如圖2所示,。

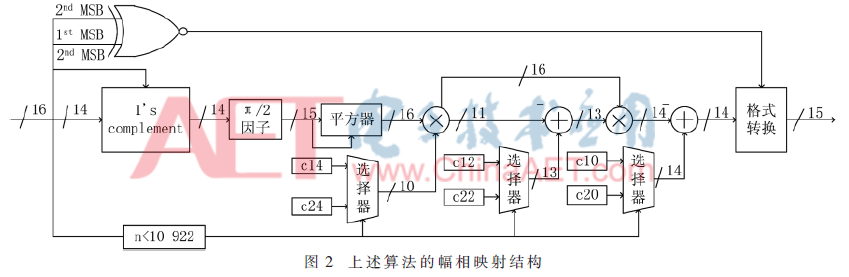
2.1 固定系數(shù)乘法器優(yōu)化

    數(shù)字電路對于2的整數(shù)次冪運(yùn)算能簡化為邏輯左移或者右移，

式中,，h_ik∈{-1,，+1}，d_ik∈{…,，-2,，-1，0,，+1,，+2，…},。M的最大值受被乘數(shù)的字長制約,，應(yīng)盡可能取小以降低結(jié)構(gòu)的復(fù)雜性。圖3所示為量化位寬為14的乘法器優(yōu)化,，其中虛線表示流水線級,。

    產(chǎn)生π/2弧度所需的固定系數(shù)乘法器如圖4所示。

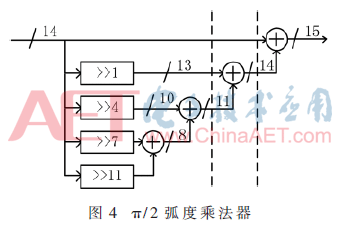
2.2 平方電路優(yōu)化

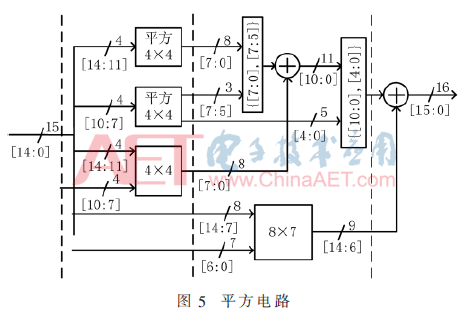
    平方運(yùn)算優(yōu)化分解為并行舍位運(yùn)算,，代替運(yùn)算后的簡單截取,，降低電路的復(fù)雜性^[10]。圖2中所需的平方電路輸入為15位,，輸出為16位,。

    改進(jìn)4級流水線的平方電路如圖5右所示。與直接截斷相比僅有1 LSB的舍入誤差,，小于2^-15,。

    量化誤差對于SFDR的影響是非線性的，利用Nelder-Mead非線性單純形法來重新計算式(12)中參數(shù),，優(yōu)化后系數(shù)見表2,。

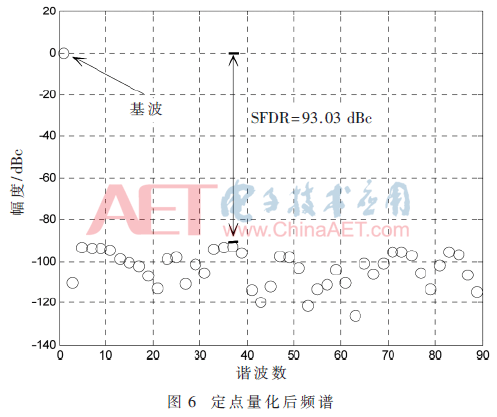
    圖6為定點(diǎn)量化后輸出信號的頻譜，SFDR為約為93.03 dbc,，與用浮點(diǎn)數(shù)計算下的理論SFDR最大值相差約2 dBc,。因此本文的設(shè)計方法可在不明顯增加硬件資源消耗的前提下,，改善合成信號的SFDR。

3 FPGA仿真與結(jié)果分析

    為了驗(yàn)證上述算法設(shè)計的結(jié)構(gòu)DDFS的有效性,，以ISE為開發(fā)平臺,，基于Xillinx spatan-6系列 XC6SLX16 FPGA進(jìn)行系統(tǒng)仿真驗(yàn)證。

    圖7為FCW=127時將程序下載到FPGA中,，利用虛擬邏輯分析儀chipscope在線采集到的波形數(shù)據(jù),。

    表3列給出了本文設(shè)計方法與其他基于FPGA的DDFS實(shí)現(xiàn)的比較。

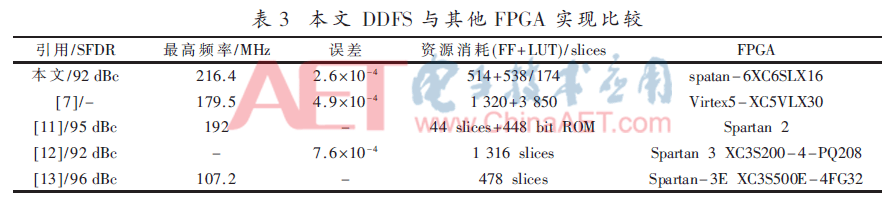
    與文獻(xiàn)[7]算法相比,，本文方法在使用更少硬件資源的情況下,，能得到輸出誤差更小，并有更大運(yùn)算頻率的輸出信號,。與文獻(xiàn)[11]～文獻(xiàn)[13]相比,，在得到同等SFDR水平下，本文所用硬件資源有所減少,，同時不影響最大運(yùn)算頻率,。

4 結(jié)論

    本文利用最小均方法得到的不等分的兩段四階偶次冪多項式為目標(biāo)函數(shù)擬合的余弦函數(shù)，可產(chǎn)生大于單段情況下約20 dBc的無雜散動態(tài)范圍,。根據(jù)所得SFDR的上界,，分析選擇最優(yōu)的相幅映射輸入和輸出位寬。優(yōu)化了固定系數(shù)乘法器和平方器,，通過Nelder-Mead非線性單純形法來減少量化,，舍入和截斷所產(chǎn)生的誤差。與理論上界差值僅為2 dBc,，同時該DDFS結(jié)構(gòu)在得到同等SFDR水平下,，與其他設(shè)計方法比減少了資源使用，該設(shè)計方法為新一代天基星載感應(yīng)式磁力儀的高精度定標(biāo)信號源提供了新的設(shè)計思路,。

參考文獻(xiàn)

[1] CAO J B，LIU Z X,，YANG J Y,，et al.First results of Low Frequency Electromagnetic Wave Detector (LFEW)[J].2005.

[2] TIERNEY J，RADER C,，GOLD B.A digital frequency synthesizer[J].IEEE Transactions on Audio and Electroacoustics,，1971，19(1)：48-57.

[3] JENG S S,，LIN H C,，LIN C H.A novel ROM compression architecture for DDFS utilizing the parabolic approximation of equi-section division.[J].IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control，2012,，59(12)：2603.

[4] GENOVESE M,，NAPOLI E,，CARO D D，et al.Analysis and comparison of Direct Digital Frequency Synthesizers implemented on FPGA[J].Integration the Vlsi Journal,，2014,，47(2)：261-271.

[5] ASHRAFI A，ADHAMI R.A direct digital frequency synthe-sizer utilizing quasi-linear interpolation method[J].IEEE Transactions on Circuits & Systems I Regular Papers,，2010,，57(4)：863-872.

[6] 衛(wèi)恒，王德功,，劉揚(yáng),，等.基于改進(jìn)DDS算法的任意信號發(fā)生器設(shè)計[J].電子技術(shù)應(yīng)用，2015,，41(6)：38-41.

[7] 祁艷杰,，劉章發(fā).基于Parallel-CORDIC的高精度高速度直接數(shù)字頻率合成器的FPGA實(shí)現(xiàn)[J].電子學(xué)報，2014,，42(7)：1392-1397.

[8] CAO Z,，SONG W，PENG Z,，et al.A high precision method for mapping phase to amplitude in direct digital synthesis and its hardware implementation[J].Review of Scientific Instruments,，2014，85(11)：1034-1043.

[9] ASHRAFI A.On the SFDR upperbound in DDFS utilizing polynomial interpolation methods[J].IEEE Transactions on Circuits & Systems II Express Briefs,，2012,，59(5)：307-311.

[10] PETRA N，CARO D D,，GAROFALO V,，et al.Truncated squarer with minimum mean-square error[J].Microelectronics Journal，2014,，45(6)：799-804.

[11] KESOULIS M,，SOUDRIS D，KOUKOURLIS C,，et al.Systematic methodology for designing low power direct digital frequency synthesisers[J].Iet Circuits Devices & Systems,，2007，1(4)：293-304.

[12] LIN K J,，CHANG C M.Design of direct digital frequency synthesizers based on unilateral second-order approximations[C]//IEEE,，International Symposium on Consumer Electronics.IEEE，2011：294-298.

[13] PRASAD N,，SWAIN A K,，MAHAPATRA K K.FPGA implementation of pipelined CORDIC based quadrature direct digital synthesizer with improved SFDR[C]//International Conference on Circuits，Power and Computing Technologies.IEEE,，2013：756-760.

作者信息:

韓  瀟1,，曾  立1,，占  豐2，陳  昱1

（1.北京航空航天大學(xué) 空間與環(huán)境學(xué)院,，北京100191,；2.山東航天電子技術(shù)研究所，山東 煙臺264000）