《電子技術(shù)應(yīng)用》
您所在的位置：首頁 > 模擬設(shè)計 > 設(shè)計應(yīng)用 > 短溝道MOSFET的毫米波噪聲建模
短溝道MOSFET的毫米波噪聲建模
2018年電子技術(shù)應(yīng)用第8期
彭小梅，趙愛峰,，王 軍
西南科技大學(xué) 信息工程學(xué)院，四川 綿陽621010
摘要： 基于40 nm MOSFET的器件物理結(jié)構(gòu),，建立了統(tǒng)一的MOSFET毫米波噪聲模型，以此來表征漏極電流噪聲,、感應(yīng)柵極電流噪聲以及兩者之間的互相關(guān)噪聲的特性,。通過將柵極過載效應(yīng)引入高頻噪聲模型，使得統(tǒng)一模型具有良好的平滑性,、準(zhǔn)確性和連續(xù)性,。最后，將所建模型的仿真結(jié)果與傳統(tǒng)的高頻噪聲模型進(jìn)行對比,，并且對比所建模型與傳統(tǒng)模型的四噪聲參數(shù)以及實(shí)測的數(shù)據(jù)來驗(yàn)證模型的有效性和精準(zhǔn)性,。
中圖分類號： TN32
文獻(xiàn)標(biāo)識碼： A
DOI：10.16157/j.issn.0258-7998.174966
中文引用格式： 彭小梅，趙愛峰,，王軍. 短溝道MOSFET的毫米波噪聲建模[J].電子技術(shù)應(yīng)用,，2018，44(8)：31-34,，38.
英文引用格式： Peng Xiaomei,，Zhao Aifeng，Wang Jun. Millimeter-wave noise modeling of nanoscale MOSFETs[J]. Application of Electronic Technique,，2018,，44(8)：31-34，38.
Millimeter-wave noise modeling of nanoscale MOSFETs
Peng Xiaomei,，Zhao Aifeng,，Wang Jun
School of Information Engineering，Southwest University of Science and Technology,，Mianyang 621010,，China
Abstract： Based on the physical structure of 40 nm MOSFETs, this paper establishes a unified MOSFET millimeter-wave noise model to characterize the characteristics of drain-current noise, inducted gate-current noise and cross-correlation noise between them. By introducing the gate overdrive effect into the high frequency noise model so that the uniform models had good smoothness, accuracy and continuity. Finally, the simulation results of the model are compared with the traditional high-frequency noise model, the validity and accuracy of the model are verified by comparing the four-noise parameters of the model with the traditional model and the measured data.
Key words : MOSFET；correlated noise,；millimeter-wave,；four noise parameters

0 引言

    隨著CMOS技術(shù)的不斷發(fā)展，傳統(tǒng)的MOSFET噪聲模型已不再符合現(xiàn)代的要求,。目前,，對于MOSFET毫米波噪聲的研究還僅限于器件的強(qiáng)反型區(qū)，而對器件弱反型區(qū)的研究少之又少,。所以,，如何建立一個完整統(tǒng)一的MOSFET毫米波噪聲模型已然成為了國內(nèi)外研究的熱點(diǎn)和難點(diǎn)。傳統(tǒng)的MOSFET高頻噪聲模型為[1]：

wdz8-gs1.gif

    通過觀察式(1)可以發(fā)現(xiàn)傳統(tǒng)的MOSFET高頻噪聲模型存在以下幾個缺點(diǎn)：漏極電流噪聲模型只考慮了溝道熱噪聲而沒有考慮散粒噪聲,；柵極感應(yīng)電流噪聲只考慮了柵極熱電阻產(chǎn)生的熱噪聲,，并沒有考慮由溝道內(nèi)的波動電勢通過柵極電容的耦合效應(yīng)引起的柵極極板的噪聲電流；互相關(guān)噪聲項并非不存在。

    本文針對以上傳統(tǒng)模型存在的缺陷,，基于40 nm MOSFET的器件物理結(jié)構(gòu)并結(jié)合電荷守恒定律,，依次提出了漏極電流噪聲模型、柵極感應(yīng)電流噪聲模型以及互相關(guān)噪聲模型,。統(tǒng)一了模型在弱反型區(qū)到強(qiáng)反型區(qū)的表達(dá)式，引入有效柵極過載效應(yīng)使得統(tǒng)一后的模型具有良好的平滑性,、準(zhǔn)確性和連續(xù)性,。最終，通過將所建模型與傳統(tǒng)的模型,、實(shí)測的數(shù)據(jù)點(diǎn)進(jìn)行對比,，驗(yàn)證模型的有效性和準(zhǔn)確性。

1 MOSFET的毫米波噪聲建模

    圖1為MOSFET小信號等效電路圖,。虛線框內(nèi)為電路的本征部分,，本征部分兩端的噪聲源分別為漏極電流噪聲源Sid以及柵極感應(yīng)電流噪聲源Sig，兩者之間的相關(guān)性通過互相關(guān)噪聲Sigid來表征,。

wdz8-t1.gif

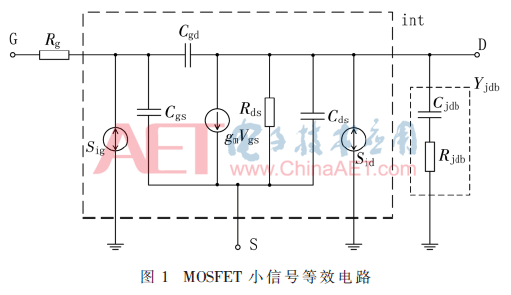
    下面就分別對漏極電流噪聲Sid,、感應(yīng)柵極電流噪聲Sig以及兩者之間的互相關(guān)噪聲Sigid進(jìn)行建模。

1.1 漏極電流噪聲

    圖2為NMOSFET的結(jié)構(gòu)示意圖,，假設(shè)溝道源區(qū)與溝道界面為電勢和坐標(biāo)的零點(diǎn),，指定源極指向漏極為x坐標(biāo)方向。設(shè)V0(x)為溝道x處的電勢,，x附近單位溝道長度的電導(dǎo)為g(x)=g(V0),，則源漏電流表達(dá)式為：

    wdz8-gs2.gif

wdz8-t2.gif

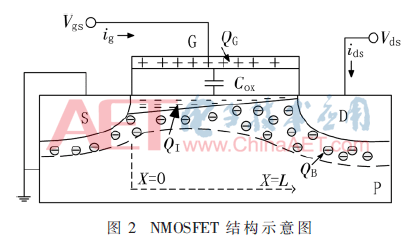
    短溝道MOSFET熱噪聲公式為：

wdz8-gs3-7.gif

其中Vds為漏源電壓，n為梯度因子,，VGT=VGS-VT為過驅(qū)動電壓,，μn為電子有效遷移率，L為有效溝道長度,，W為溝道寬度,，Voff為補(bǔ)償電壓，Vth=kT/q為熱電壓,。

    當(dāng)器件工作在毫米波段時,，根據(jù)文獻(xiàn)[2]的報導(dǎo)可知MOSFET的p-n結(jié)的散粒噪聲為：

    wdz8-gs8.gif

式中4kTg是附加噪聲分量，g為增量電導(dǎo),。由式(8)可得MOSFET工作在毫米波段時的漏極電流噪聲表達(dá)式：

wdz8-gs9-10.gif

wdz8-gs11-14.gif

式中δ為電荷系數(shù),。

    當(dāng)器件工作在強(qiáng)反型區(qū)時，因不考慮襯底效應(yīng),，VGTeff可變?yōu)閂GT,。等效電路模型下的柵極電阻也影響漏極電流噪聲，所以強(qiáng)反型區(qū)下的漏極電流噪聲可表示為：

wdz8-gs15-16.gif

1.2 感應(yīng)柵極電流噪聲

    感應(yīng)柵極電流噪聲包含柵極電阻產(chǎn)生的熱噪聲，以及由溝道內(nèi)的波動電勢通過柵極電容的耦合效應(yīng)而引起的柵極極板的噪聲電流[4],。

    如圖2所示,，柵極感應(yīng)噪聲電流可表示為：

    wdz8-gs17.gif

式中φS(x)為沿著溝道方向x處電勢，ω為角頻率,。隨著溝道長度的減小,，溝道中漏源結(jié)的耗盡層占據(jù)比重加大，柵下硅表面形成的電荷量減少,。當(dāng)器件處于弱反型區(qū)時,，溝道電流以擴(kuò)散電流為主[5]，所以弱反型區(qū)的漏極電流為：

wdz8-gs18-21.gif

    當(dāng)器件工作在弱反型區(qū)時,，反型層電荷濃度和耗盡層電荷濃度相比可以忽略不計,，從源端到漏端的表面勢可視為常數(shù)，通過求解泊松方程可得到溝道反型層電子密度為：

wdz8-gs22-25.gif

1.3 互相關(guān)噪聲

    漏極電流噪聲源和柵極感應(yīng)噪聲源都與偏置和載流子運(yùn)動有關(guān),，由于柵-源電壓的正電場吸引,，使溝道中的載流子穿過多晶而到達(dá)柵極板間，所以電荷間的耦合作用促使了互相關(guān)噪聲的形成,。根據(jù)式(20)可以建立互相關(guān)噪聲模型：

wdz8-gs26-27.gif

式中α為互相關(guān)噪聲系數(shù),，這里同樣為了模型能在弱反型區(qū)和強(qiáng)反型區(qū)都適用，引入有效柵極過載效應(yīng),。式(27)可轉(zhuǎn)化為：

wdz8-gs28-29.gif

2 結(jié)果與分析

    首先,，利用MATLAB軟件對本文提出的數(shù)學(xué)模型進(jìn)行仿真，將仿真結(jié)果與傳統(tǒng)模型仿真結(jié)果作比較,，如圖3所示,。

wdz8-t3.gif

    圖3為所建模型以及傳統(tǒng)模型的Sid、Sig和Sigid*關(guān)于柵極過載電壓的曲線圖,。圖中實(shí)線代表著本文模型,；虛線代表著傳統(tǒng)模型。通過圖3中的曲線對比可以觀察出：圖3(a)中的傳統(tǒng)模型不適用于器件的弱反型區(qū)而本文模型可以,，在強(qiáng)反型區(qū)本文的模型與傳統(tǒng)模型的走勢大體一致,；圖3(b)中兩個模型的仿真結(jié)果有著一樣的變化趨勢；圖3(c)中所建模型的仿真結(jié)果體現(xiàn)出了漏極電流噪聲與柵極感應(yīng)噪聲之間的相關(guān)性,，而傳統(tǒng)模型則無法表征其相關(guān)性,。由此可見本文所建的模型要優(yōu)于傳統(tǒng)模型。

    然后,，本文基于HP8510網(wǎng)絡(luò)分析儀和ATNnp5b微波噪聲參數(shù)系統(tǒng)的實(shí)驗(yàn)平臺,，對柵指數(shù)Nf=10、柵寬W為2 μm,、柵長L為45 nm,、并聯(lián)設(shè)備數(shù)M為6的MOSFET進(jìn)行S參數(shù)的測量以及噪聲系數(shù)F50的測量。再分別提取出[6]器件四噪聲參數(shù)Rn、Fmin,、Gopt,、Bopt的測量值。

    利用本文提出的Sid,、Sig以及Sigid*模型,，根據(jù)式(30)～式(33)，可得四噪聲參數(shù)的仿真計算結(jié)果[4],。如圖4所示,，通過比較測量值與仿真結(jié)果的一致性，驗(yàn)證本文所建模型的有效性和精確性,。

wdz8-t4.gif

    wdz8-gs30.gif

    wdz8-gs31-33.gif

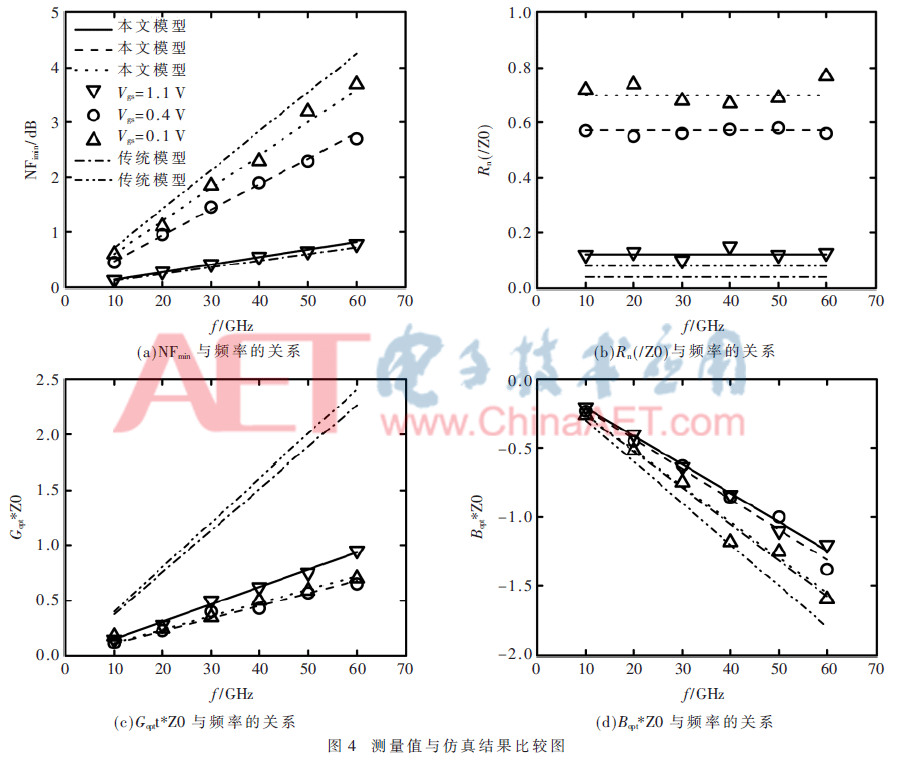
    圖4為本文模型在不同反型區(qū)，不同頻率點(diǎn)下與傳統(tǒng)模型以及實(shí)測數(shù)據(jù)點(diǎn)的四噪聲參數(shù)對比曲線圖,。實(shí)線,、短線、點(diǎn)線分別代表所建模型在弱反型區(qū),、中反型區(qū),、強(qiáng)反型區(qū)的仿真結(jié)果；倒三角,、圓圈,、正三角分別代表著分布在弱反型區(qū)、中反型區(qū),、強(qiáng)反型區(qū)的實(shí)測數(shù)據(jù)點(diǎn),；線點(diǎn)線、線點(diǎn)點(diǎn)線分別代表傳統(tǒng)模型在中反型區(qū)和強(qiáng)反型區(qū)的仿真結(jié)果,。通過觀察圖4發(fā)現(xiàn)：本文所建模型的仿真結(jié)果在各個反型區(qū)都能與實(shí)測數(shù)據(jù)點(diǎn)相吻合,，而傳統(tǒng)模型不適用于弱反型區(qū)，并且在弱反型區(qū)和強(qiáng)反型區(qū)中它的變化趨勢雖與實(shí)測數(shù)據(jù)相一致,，但精度遠(yuǎn)不如本文所建模型,。

3 結(jié)論

    本文通過對傳統(tǒng)模型不足的分析，基于40 nm MOSFET的物理結(jié)構(gòu),，重新建立了漏極電流噪聲模型,、柵極電流噪聲模型以及兩者的互相關(guān)模型。同時引入柵極過載效應(yīng),使得各模型的統(tǒng)一表達(dá)式在弱反型區(qū)到強(qiáng)反型區(qū)之間具有良好的平滑性,。最后,，通過對比不同反型區(qū)下的所建模型、傳統(tǒng)模型以及實(shí)測點(diǎn)的四噪聲參數(shù),，驗(yàn)證了本文模型的有效性和精準(zhǔn)性,。

參考文獻(xiàn)

[1] NAVID R，JUNGEMANN C，LEE T H,，et al.High frequency noise in nanoscale MOSFETs[J].J.Appl.Phys.2007,，101：124501.

[2] ANTONOPOULOS A，BUCHER M,，PAPATHANASIOU K,，et al.CMOS small-signal and thermal noise modeling at high frequencies[J].IEEE Trans.Electron Devices，2013,，60：3727-3733.

[3] CHAN L H K,，YEO K S，CHEW K W J,，et al.MOSFET drain current noise modeling with effective gate overdrive and junction noise[J].IEEE Electron Device Letters,，2012，33(8)：1117-1119.

[4] CHAN L H K,，YEO K S,，CHEW K W J，et al.High-frequency noise modeling of MOSFETs for ultra low-voltage RF applications[J].IEEE Trans.Microw. Theory Techn.,，2015,，63：141-153.

[5] SPATHIS C，BIRBAS A,，GEORGAKOPOULOU K.Semi-classical noise investigation for sub-40nm metal-oxide-semiconductor field effect[J].AIP Advances,，2015，5：087114.

[6] LEE C I,，LIN W C,，LIN Y T.An improved cascade based noise de-embedding method for on-wafer noise parameter measurement[J].IEEE Trans.Electron Devices Lett.，2015,，36：291-293.



作者信息:

彭小梅,，趙愛峰，王  軍

（西南科技大學(xué) 信息工程學(xué)院,，四川 綿陽621010）

此內(nèi)容為AET網(wǎng)站原創(chuàng),，未經(jīng)授權(quán)禁止轉(zhuǎn)載。