0 引言

    MEMS慣性器件因具有低成本、輕重量,、小體積,、低功耗等優(yōu)勢在民用和軍用方面都有廣泛的應(yīng)用^[1-3]。傳統(tǒng)的捷聯(lián)慣導(dǎo)粗對準(zhǔn)方法是利用陀螺儀與加速度計信息通過解析法確定初始姿態(tài)矩陣^[4],，而對于MEMS陀螺儀,，其輸出信噪比低、漂移大等問題直接影響了捷聯(lián)慣導(dǎo)系統(tǒng)初始對準(zhǔn)的準(zhǔn)確性和可行性。

    捷聯(lián)慣導(dǎo)系統(tǒng)因其重要的實(shí)用價值在國內(nèi)外有許多專家學(xué)者也在研究其初始對準(zhǔn)方式以期提高精度和對準(zhǔn)速度,。文獻(xiàn)[5]提出了一種磁強(qiáng)計輔助基于MEMS慣性器件SINS的初始對準(zhǔn)方法,，通過構(gòu)造3個相互正交的向量間接對準(zhǔn)，減小了計算量,；文獻(xiàn)[6]提出基于線性最優(yōu)控制的捷聯(lián)慣導(dǎo)對準(zhǔn)方法,；文獻(xiàn)[7]提出捷聯(lián)慣導(dǎo)系統(tǒng)雙矢量定姿的方法?；谝陨涎芯?，本文提出一種多遺忘因子自適應(yīng)卡爾曼濾波(Multi Forgetting Factors Adaptive Kalman Filter, MFFAKF)的MEMS間接粗對準(zhǔn)方法，在對加速度計和磁力計數(shù)據(jù)進(jìn)行優(yōu)化的同時通過合理地構(gòu)造正交矢量減小初始對準(zhǔn)時的姿態(tài)角計算量,，以提高對準(zhǔn)精度和對準(zhǔn)速度,，并對該方法進(jìn)行了分析驗證。

1 磁輔助間接粗對準(zhǔn)

MEMS慣導(dǎo)系統(tǒng)在進(jìn)入導(dǎo)航狀態(tài)之前,，需要進(jìn)行初始對準(zhǔn),，即載體坐標(biāo)系（b系）轉(zhuǎn)換到導(dǎo)航坐標(biāo)系（n系）的初始姿態(tài)矩陣：

2 MFFAKF降噪

    多遺忘因子遺忘濾波算法在濾波的過程中放大了系統(tǒng)噪聲Q_k和量測噪聲R_k，在建模不準(zhǔn)的情況下改善了濾波精度,，但同時放大噪聲也增大了系統(tǒng)的不確定性,，并且通過開窗法求得的遺忘因子是對歷史數(shù)據(jù)求取算數(shù)平均值，并不能增加新近信息的權(quán)重,。為了在強(qiáng)調(diào)新近信息的同時改善系統(tǒng)的穩(wěn)定性,，在狀態(tài)估計的同時通過量測輸出在線實(shí)時估計系統(tǒng)的噪聲參數(shù)，本文提出一種改進(jìn)型多遺忘因子自適應(yīng)卡爾曼濾波方法,，由于估計所有的噪聲參數(shù)往往比較困難,，因此本文使用多遺忘因子對量測噪聲方差陣進(jìn)行調(diào)整，并且采用指數(shù)漸消記憶的加權(quán)方式實(shí)時估計量測噪聲方差陣,，使用陳舊數(shù)據(jù)的利用率以遺忘因子的指數(shù)次方遞減,，增大新近信息的使用率。

    若記加權(quán)系數(shù)β_k,，i,，b為遺忘因子(0<b<1)，有如下因式分解公式成立：

    從式(12)可以看出,，將β_k,，i加入濾波過程，對陳舊數(shù)據(jù)的利用率將以b的指數(shù)次方遞減,，所有數(shù)據(jù)的權(quán)值總和為1,。

    β_k，k表示k時刻最新數(shù)據(jù)的加權(quán)系數(shù),，簡記為β_k,，則β_k的遞推公式為：

3 實(shí)驗結(jié)果及分析

    實(shí)驗采用慣性測量單元（MTI-G）獲取數(shù)據(jù),。三軸慣性測試轉(zhuǎn)臺可以提供姿態(tài)角作為參考基準(zhǔn)，實(shí)驗所處位置的磁偏角為1°,。實(shí)驗系統(tǒng)實(shí)物圖如圖1所示,。其中，本文主要用到MTI-G中的加速度計和磁強(qiáng)計,，其主要技術(shù)參數(shù)如表1所示,。 

    設(shè)備啟動后置水平位靜置1 h后，開始采集數(shù)據(jù),，5 min后停止采集。為驗證本文所提出算法的可行性和穩(wěn)定性,，設(shè)計完全靜止和受擾動情況下的粗對準(zhǔn)實(shí)驗,。實(shí)驗設(shè)計為對采集的數(shù)據(jù)分別進(jìn)行原始數(shù)據(jù)的粗對準(zhǔn)實(shí)驗和MFFAKF對采集的數(shù)據(jù)處理后的粗對準(zhǔn)實(shí)驗。將對準(zhǔn)后的姿態(tài)角誤差進(jìn)行對比分析,。

    在粗對準(zhǔn)過程中,，系統(tǒng)的結(jié)構(gòu)參數(shù)和噪聲統(tǒng)計特性都不是準(zhǔn)確已知的，且加速度計和磁強(qiáng)計的輸出易受溫度,、磁場干擾等外界環(huán)境的影響,，所以實(shí)驗設(shè)定濾波的量測噪聲遠(yuǎn)大于系統(tǒng)噪聲，系統(tǒng)陣Φ與量測陣H都為單位陣,，系統(tǒng)初值設(shè)定為0,，多遺忘因子卡爾曼濾波中的遺忘因子設(shè)定為：

    s^N=diag{1.018，1.01,，1.01,，1.025}

    以慣性導(dǎo)航實(shí)驗系統(tǒng)提供的姿態(tài)角作為參考基準(zhǔn)，使用2種方法所得的對準(zhǔn)3個姿態(tài)角誤差對比曲線分別如圖2(a),、圖2(b),、圖2(c)所示。

    如圖2所示,，在完全靜止實(shí)驗中,，只采用磁力計輔助對準(zhǔn)的情況下解算結(jié)果波動明顯，且與參考數(shù)據(jù)間存在較大誤差,，而采用MFFAKF降噪輔助對準(zhǔn)解算出的滾轉(zhuǎn)角與俯仰角也存在一定程度上的波動,，但基本與參考數(shù)據(jù)的波動狀態(tài)一致，其偏離范圍也遠(yuǎn)小于只采用磁力計輔助方式的數(shù)據(jù),，而航向角的解算結(jié)果組合算法的結(jié)果明顯優(yōu)于磁力計輔助算法的結(jié)果,，這是因為滾轉(zhuǎn)角和俯仰角的解算過程只使用了加速度計的數(shù)據(jù)，而航向角的解算需要用到磁力計的數(shù)據(jù),，而磁力計的去噪效果遠(yuǎn)優(yōu)于加速度計的去噪效果,，因此使得解算后的航向角相比單算法的結(jié)果更加平滑。這主要是由于此方法能夠較為快速地適應(yīng)姿態(tài)角的變化，對新近信息的利用率較高,，具有良好的自適應(yīng)能力,。

    為進(jìn)一步驗證本文提出的MFFAKF算法對MEMS慣導(dǎo)系統(tǒng)粗對準(zhǔn)精度與穩(wěn)定性影響，分別將2種方法的比對結(jié)果進(jìn)行分析,，如表2所示,。

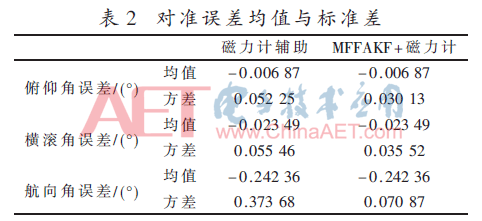
    由表2可以看出，只使用磁力計輔助粗對準(zhǔn)與MFFAKF去噪+磁力計輔助粗對準(zhǔn)相對于參考數(shù)據(jù)差值的均值是一樣的,，且俯仰角誤差為0.006 87°,，橫滾角誤差為0.023 49°，航向角誤差為0.242 36°,，其均在實(shí)驗設(shè)備的誤差范圍內(nèi),，因此可以認(rèn)為兩種方法得到的航向角均為真實(shí)值。但采用MFFAKF降噪處理后獲得的姿態(tài)角相對于參考數(shù)據(jù)偏差更小,，且曲線更為平滑,，其粗對準(zhǔn)的結(jié)果在所列方法中最接近真實(shí)值且波動范圍最小。其水平姿態(tài)角誤差和航向角誤差均值均滿足慣導(dǎo)系統(tǒng)粗對準(zhǔn)后姿態(tài)角誤差小于1°的要求,，此結(jié)果對MEMS慣導(dǎo)系統(tǒng)進(jìn)行精對準(zhǔn)提供了保障,。

4 結(jié)論

    本文提出一種MFFAKF+磁力計輔助的MEMS慣導(dǎo)系統(tǒng)粗對準(zhǔn)方案。通過對MEMS傳感器輸出處理,，強(qiáng)調(diào)新近信息對濾波過程的影響,，使其能自適應(yīng)載體的姿態(tài)變化。實(shí)驗結(jié)果表明,，粗對準(zhǔn)結(jié)果俯仰角誤差為0.006 87°,，橫滾角誤差為0.023 49°，航向角誤差為0.242 36°,，均在實(shí)驗設(shè)備的誤差范圍內(nèi),，滿足粗對準(zhǔn)的精度要求，對實(shí)際工程應(yīng)用提供一定的參考價值,。

參考文獻(xiàn)

[1] Sun Wei,，Wang Daxue，Xu Longwei,，et al.MEMS-based rotary strapdown inertial navigation system[J].Measurement,，2013，46(8)：2585-2596.

[2] 劉大鵬,，馬曉川,，朱昀.磁強(qiáng)計輔助實(shí)現(xiàn)捷聯(lián)慣導(dǎo)初始對準(zhǔn)[J].壓電與聲光，2010,，32(2)：229-232.

[3] 馮培德,，李魁,，王瑋.一種新的艦載慣導(dǎo)系統(tǒng)搖擺基座初始對準(zhǔn)方法[J].儀器儀表學(xué)報，2012,，33(1)：1-6.

[4] MALAKAR B,，ROY B K.A novel application of adaptive filtering for initial alignment of Strapdown Inertial Navigation System[C].International Conference on Circuits，Systems,，Communication and Information Technology Applications.IEEE,，2014：189-194.

[5] 高勇，曹娟娟,，唐海紅,，等.磁強(qiáng)計輔助基于MEMS慣性器件SINS的初始對準(zhǔn)方法研究[J].航天控制，2013,，31(3)：50-54.

[6] 錢華明,，葛磊，彭宇.多漸消因子卡爾曼濾波及其在SINS初始對準(zhǔn)中的應(yīng)用[J].中國慣性技術(shù)學(xué)報,，2012，20(3)：287-291.

[7] 張劍慧,，秦永元,，龍瑞.捷聯(lián)慣導(dǎo)系統(tǒng)雙矢量定姿方法研究[J].計算機(jī)測量與控制，2010,，18(11)：2634-2637.

作者信息:

孫  佳,，鄒  靖，胡  桐

（齊魯工業(yè)大學(xué)（山東省科學(xué)院） 山東省科學(xué)院海洋儀器儀表研究所

山東省海洋環(huán)境監(jiān)測技術(shù)重點(diǎn)實(shí)驗室,，山東 青島266001）