文獻標(biāo)識碼:A
DOI: 10.19358/j.issn.2096-5133.2018.07.009
中文引用格式:劉云濤.基于蝴蝶優(yōu)化的粒子濾波算法[J].信息技術(shù)與網(wǎng)絡(luò)安全,2018,37(7):37-41.
0 引言
粒子濾波是一種基于蒙特卡羅思想的非線性非高斯?fàn)顟B(tài)估計濾波方法[1],在故障診斷、目標(biāo)跟蹤等相關(guān)領(lǐng)域取得了一定的應(yīng)用效果。段琢華等人[2]提出一種基于粒子濾波器的移動機器人傳感器故障診斷方法,并驗證了該方法可以有效識別移動機器人一種或多種故障。程建等人[3]將粒子濾波理論應(yīng)用于紅外目標(biāo)跟蹤,在粒子濾波理論框架下,紅外目標(biāo)的狀態(tài)后驗概率分布用加權(quán)隨機樣本集表示,通過隨機樣本的Bayesian迭代進化實現(xiàn)紅外目標(biāo)的跟蹤。然而隨著迭代次數(shù)的增加,粒子重要性權(quán)重的方差越來越大,使得粒子的權(quán)重集中到很少數(shù)粒子上,其他粒子的重要性權(quán)值將會很小,這就是粒子退化現(xiàn)象。DOUCET A等人[4]已從理論上證明了粒子退化現(xiàn)象出現(xiàn)的必然性。粒子退化問題將會嚴(yán)重影響粒子濾波精度。
針對粒子濾波存在的粒子退化問題,國內(nèi)外學(xué)者進行了大量的研究。張琪等人[5]提出一種基于權(quán)值選擇的粒子濾波算法.按照粒子權(quán)值的大小選擇較好的粒子用于濾波,以增加樣本的多樣性,從而緩解粒子濾波的退化問題。夏飛等人[6]在重采樣階段采用了一種權(quán)值排序、優(yōu)勝劣汰的重采樣算法,對各粒子的歸一化權(quán)值按從小到大的順序排列,并根據(jù)權(quán)值方差大小淘汰粒子,從而得到了改進的粒子濾波算法,在一定程度上解決了標(biāo)準(zhǔn)粒子濾波的退化問題。但是上述兩種方法仍然是基于傳統(tǒng)采樣的框架,未能徹底解決粒子退化的問題。
蝴蝶算法(Butterfly Algorithm,BA)是由ARORA S和SINGH S[7]提出的一種基于蝴蝶覓食行為的全局優(yōu)化算法。通過仿真指出該算法優(yōu)于其他自然啟發(fā)式算法,相較于其他算法具有更高的收斂精度和更快的收斂速度。受此算法特點啟發(fā),本文引入蝴蝶算法優(yōu)化粒子濾波采樣過程,并通過仿真實驗驗證蝴蝶優(yōu)化粒子濾波算法能夠改善基本粒子算法存在的濾波粒子退化問題。
1 粒子濾波算法
粒子濾波是一種基于蒙特卡羅思想的貝葉斯估計方法 [8]。假設(shè)有非線性系統(tǒng)的狀態(tài)空間模型:

其中,f(·)和h(·)分別為狀態(tài)轉(zhuǎn)移方程和觀測方程。xt為系統(tǒng)在t時刻的狀態(tài)變量,zt為系統(tǒng)在t時刻的觀測值,wt和vt為相互獨立的噪聲,分別為系統(tǒng)的過程噪聲和觀測噪聲,ut為系統(tǒng)在t時刻的輸入量。
濾波就是計算后驗濾波概率密度p(xt|z1:t),已知p(xt|z1:t)是p(x0:t|z1:t)的邊沿概率密度。假設(shè)t-1時刻濾波概率密度p(xt-1|z1:t-1)已知,系統(tǒng)狀態(tài)xt服從一階馬爾可夫過程且系統(tǒng)觀測zt獨立。通過下式

得出包含t-1時刻觀測值的t時刻系統(tǒng)狀態(tài)先驗概率密度p(xt|z1:t-1):
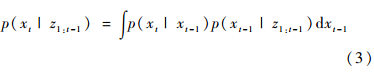
式(3)即為預(yù)測過程,其中,p(xt|xt-1)是系統(tǒng)的狀態(tài)轉(zhuǎn)移概率密度。利用t時刻的觀測值zt,通過更新修正p(xt|z1:t-1),得到t時刻系統(tǒng)狀態(tài)的后驗概率密度p(xt|z1:t),由貝葉斯定理可得狀態(tài)更新方程:

其中
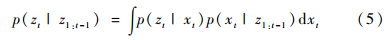
然而,對于非線性非高斯系統(tǒng)而言,在過程中式(3)和式(4)消去中間參量和其他位置參量的計算卻很困難,很難得到完整的解析式來表達這樣的概率密度函數(shù)。因此,粒子濾波采用序貫蒙特卡羅采樣方法,從后驗概率密度p(xt|z1:t)采樣大量的隨機樣本點來近似待估計的分布,這些隨機樣本點稱為粒子。用大量的粒子來近似整個后驗分布,當(dāng)粒子數(shù)量足夠多時,后驗分布能被準(zhǔn)確近似,是一種全局近似最優(yōu)濾波。假設(shè)從后驗概率密度p(xt|z1:t)采樣得到N個粒子,則后驗概率密度可以通過下式近似表示:

其中,xit表示從后驗概率密度中采樣得到的粒子,δ(·)表示Dirac delta函數(shù)。
但是在實際中卻很難從函數(shù)p(xt|z1:t)中采樣。可以先從一個事先已知且容易采樣的參考分布q(xt|z1:t)中采樣,通過在q(xt|z1:t)中采樣x粒子進行加權(quán)來近似計算p(xt|z1:t)。當(dāng)選取重要概率密度為
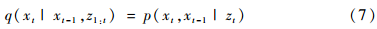
時,重要性權(quán)重方差最小,此時為最優(yōu)重要性概率密度。權(quán)值計算方程為:
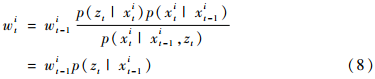
式(8)中,p(zt|xit-1)無法求解,所以更常見的是選取先驗概率密度為重要性概率密度,即

式子化簡為

將重要性權(quán)重歸一化,即

而后驗概率密度可以表示為:

式中,重要性權(quán)值如式(11)所示。當(dāng)N→∞時,由大數(shù)定理可知,式(12)逼近于真實后驗概率p(xt|z1:t)。
2 蝴蝶優(yōu)化粒子濾波
2.1 蝴蝶算法
蝴蝶算法是一種自然啟發(fā)式全局尋優(yōu)算法,其主要思想類似于蝴蝶群覓食行為,每一只蝴蝶都會散發(fā)一定強度的香味,同時每只蝴蝶都會感受到周圍其它蝴蝶的香味,并朝著那些散發(fā)更多香味的蝴蝶移動。蝴蝶的香味取決于三個因素:感知形態(tài)、刺激強度以及冪指數(shù)。用方程表示為
F=cIa(13)
其中,F(xiàn)表示香味濃度大小,c為感知形態(tài),I為刺激強度,a為冪指數(shù)。
已知目標(biāo)函數(shù)f(x),蝴蝶算法的基本步驟如下:
(1)初始化具有n只蝴蝶的蝴蝶種群,由目標(biāo)函數(shù)f(xi)決定每一只蝴蝶xi的刺激強度Ii。
(2)計算蝴蝶種群中每一只蝴蝶的適應(yīng)值,并找到位置最優(yōu)的蝴蝶。
(3)計算蝴蝶散發(fā)的香味。由于外界環(huán)境的干擾,產(chǎn)生隨機數(shù)p用于決定蝴蝶是進行局部搜索還是全局搜索。
(4)若進行全局搜索,蝴蝶飛向全局適應(yīng)度最高的蝴蝶,全局搜索可以表示為

其中,xt+1i為第i只蝴蝶在第t次迭代的解向量。g*表示目前所有蝴蝶中的最優(yōu)解。
(5)若進行局部搜索,蝴蝶進行Lévy隨機飛行。局部搜索可以表示為


為了避免蝴蝶移動陷入局部最優(yōu),在算法中引入Lévy飛行,Lévy飛行實質(zhì)是一種隨機游走,步長分布符合重尾概率分布:
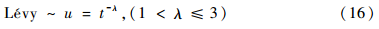
Lévy飛行能夠加快局部搜索,提高搜索效率。本文中,λ的取值范圍為(1,2]。
2.2 融合蝴蝶算法與粒子濾波
在蝴蝶算法中,把蝴蝶看作粒子濾波中的粒子,可以看出蝴蝶算法和粒子濾波存在一定的相似性。首先,蝴蝶算法中蝴蝶不斷地更新自己的位置并向適應(yīng)度最高的蝴蝶飛去,類似于粒子濾波算法中粒子不斷地逼近真實系統(tǒng)狀態(tài)的后驗概率分布。其次,蝴蝶算法中適應(yīng)度最高的蝴蝶是種群中的最優(yōu)值,類似于粒子濾波算法中具有最大重要性權(quán)重的粒子最可能處于真實的后驗分布。
本文將蝴蝶算法優(yōu)化思想引入粒子濾波采樣過程,提高粒子濾波性能。但是如果直接將蝴蝶優(yōu)化算法與粒子濾波結(jié)合,會導(dǎo)致許多的問題,所以引入蝴蝶算法優(yōu)化粒子濾波的過程中需做如下修改:
(1)常規(guī)粒子濾波的重要性概率密度選取的是先驗概率密度,丟失了當(dāng)前時刻的觀測值,所以在計算蝴蝶的適應(yīng)值時利用最新時刻的觀測值。因此,計算蝴蝶的適應(yīng)值方程定義為:

其中,Rk是觀測噪聲方差,znew是最新的觀測值,zpred表示預(yù)測的觀測值。
(2)在蝴蝶的移動過程中,每一只蝴蝶都會向當(dāng)前已知最優(yōu)值逼近。而在蝴蝶算法的全局搜索方程中g(shù)*-xti已經(jīng)確定了蝴蝶的移動方向,但是當(dāng)Lévy飛行出現(xiàn)負(fù)值時,蝴蝶卻會朝著最優(yōu)值反方向移動,造成無效的重復(fù)計算。因此,應(yīng)對Lévy飛行取絕對值。改進后的全局搜索方程變?yōu)?

(3)在蝴蝶算法的全局搜索方程式(18)和局部搜索方程式(15)中,當(dāng)Lévy飛行值和Fi值太小時會導(dǎo)致蝴蝶的位置基本不移動,造成無效的位置更新。所以當(dāng)蝴蝶更新的位移太小時需要根據(jù)實際情況進行適當(dāng)?shù)臄U大。
綜上,引入蝴蝶算法優(yōu)化后的粒子濾波(BA-PF)具體實現(xiàn)如下:
(1)初始化。選取先驗概率作為重要性概率密度函數(shù),從重要性函數(shù)中產(chǎn)生N個粒子組成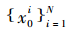 粒子群,所有粒子的權(quán)值為1/N。設(shè)置迭代次數(shù)T、搜索切換概率p等參數(shù)。
粒子群,所有粒子的權(quán)值為1/N。設(shè)置迭代次數(shù)T、搜索切換概率p等參數(shù)。
(2)預(yù)測。通過式(1)計算狀態(tài)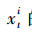 的預(yù)測值
的預(yù)測值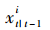 。
。
(3)尋找最優(yōu)值。把粒子濾波中的每一個粒子看作蝴蝶算法中的一只蝴蝶。通過適應(yīng)度函數(shù)式(17)計算每一個粒子的適應(yīng)度值,并通過式(19)找到全局最優(yōu)的粒子g*,即適應(yīng)度值最大的蝴蝶。

(4)利用式(13)計算每一個粒子的香味Fi,產(chǎn)生隨機數(shù)r用以決定粒子利用式(18)進行全局搜索,或者利用式(16)進行局部搜索。當(dāng)?shù)螖?shù)達到最大次數(shù)M時,停止迭代。
(5)更新優(yōu)化后粒子的重要性權(quán)重并歸一化。
(6)重采樣。若有效粒子Neff小于有效樣本閾值Nth,即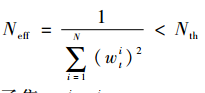 時,則進行重采樣。得到新的粒子集
時,則進行重采樣。得到新的粒子集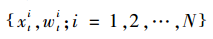 。
。
(7)狀態(tài)估計。利用 進行狀態(tài)估計。
進行狀態(tài)估計。
(8)判斷算法是否繼續(xù),若繼續(xù),則返回步驟(2),否則算法結(jié)束。
3 實驗結(jié)果及分析
實驗硬件環(huán)境為筆記本電腦(Intel Core i7處理器、16 GB內(nèi)存),實驗軟件環(huán)境為MATLAB 2016a。為了驗證改進粒子濾波的有效性,將蝴蝶優(yōu)化粒子濾波算法(BA-PF)與常規(guī)粒子濾波(PF)和基于無跡卡爾曼濾波優(yōu)化的粒子濾波(UPF)進行對比,本文采用文獻[9]中的非線性系統(tǒng),系統(tǒng)的狀態(tài)方程和測量方程為:

其中φ1=0.5,φ2=0.2,φ3=0.5,ξ=0.04,過程噪聲w取Gamma(3,2)的伽瑪噪聲,觀測噪聲v取均值為零、方差為0.000 1的高斯噪聲。采用3種算法對上述非線性模型系統(tǒng)狀態(tài)進行估計和跟蹤。采用均方根誤差ERMSE來度量各濾波算法的性能。均方根誤差公式為:


實驗算法參數(shù)設(shè)置值參考如表1所示。
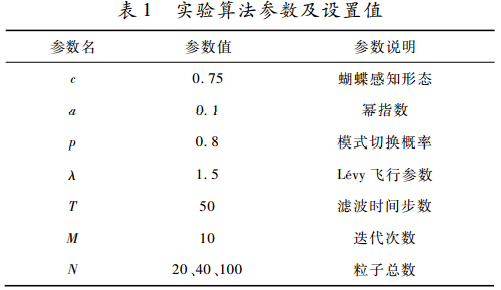
仿真在不同粒子數(shù)N=20、N=40、N=100下對三種粒子濾波算法的濾波精度和運行時間進行對比,如表2所示。圖1為一次獨立仿真條件下粒子數(shù)N=20時三種粒子濾波算法的狀態(tài)估計,圖2為對應(yīng)仿真運行中三種粒子濾波算法的估計誤差絕對值。

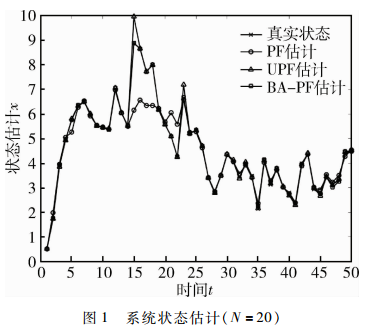
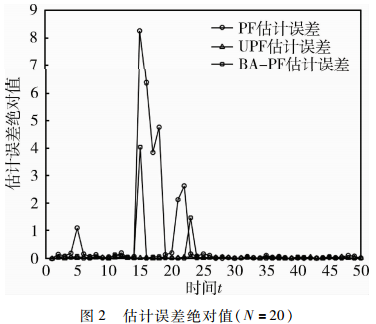
由圖1、圖2和表2可以看出,BA-PF算法的均方根誤差明顯小于PF算法和UPF算法,同時BA-PF算法在粒子數(shù)較少時就能具有很高的濾波精度,這主要是因為BA-PF算法能夠驅(qū)動無效粒子向似然概率高的區(qū)域移動,增強了粒子的作用效果。而PF算法在粒子數(shù)量較少時,容易失去狀態(tài)估計,如從時間點t=16到t=22。UPF因為引入無跡卡爾曼濾波,所以濾波精度較PF算法有所提高,但是低于BA-PF算法的濾波精度。
為了測試不同粒子濾波算法的魯棒性,獨立仿真在時間點t=40和t=45時刻設(shè)置狀態(tài)發(fā)生的突變,幅值為15。圖3為粒子數(shù)N=20并且發(fā)生突變后三種粒子濾波算法的狀態(tài)估計結(jié)果,圖4為相應(yīng)三種粒子濾波算法的估計誤差絕對值。從表2中還可知,BA-PF算法的執(zhí)行時間稍微高于PF算法,但是遠(yuǎn)低于UPF算法的執(zhí)行時間。

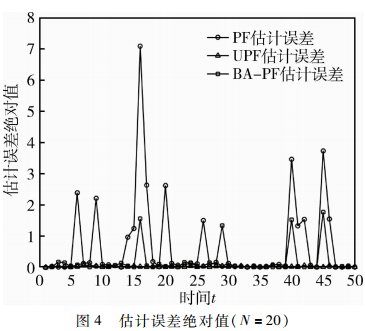
從圖3和圖4可以看出在t=40和t=45時刻狀態(tài)值發(fā)生躍變,PF算法和UPF算法都發(fā)生了明顯的估計偏差,其中又以PF算法最為明顯。而BA-PF算法由于引入Lévy隨機飛行,避免了局部最優(yōu)問題,沒有發(fā)生明顯偏差,這說明BA-PF算法對系統(tǒng)狀態(tài)突變的適應(yīng)性強,算法魯棒性高。綜上,由于BA-PF算法在重要性采樣過程中引入蝴蝶優(yōu)化算法,有效改善了粒子退化現(xiàn)象,提高了濾波精度。
4 結(jié)論
本文提出了一種基于蝴蝶優(yōu)化的粒子濾波算法,引入蝴蝶算法優(yōu)化常規(guī)粒子濾波的重要性采樣過程,驅(qū)動遠(yuǎn)離真實狀態(tài)的粒子向真實狀態(tài)可能性較大的區(qū)域移動,從而有效改善了粒子濾波存在的粒子退化問題,提高了粒子濾波的濾波精度。同時通過蝴蝶搜索模式的切換和Lévy隨機飛行使BA-PF算法避免陷入局部最優(yōu)。實驗結(jié)果表明,BA-PF算法在粒子數(shù)量少量的情況下能實現(xiàn)有效濾波,比PF算法具有更好的濾波性能,算法魯棒性高。
參考文獻
[1] PARK S, HWANG J P, KANG H J, et al. A new evolutionary particle filter for the prevention of sample impoverishment[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(4):801-809.
[2] 段琢華, 蔡自興, 于金霞,等. 基于粒子濾波器的移動機器人慣導(dǎo)傳感器故障診斷[J]. 中南大學(xué)學(xué)報(自然科學(xué)版), 2005, 36(4):642-647.
[3] 程建, 周越, 蔡念,等. 基于粒子濾波的紅外目標(biāo)跟蹤[J]. 紅外與毫米波學(xué)報, 2006, 25(2):113-117.
[4] DOUCET A, GODSILL S, ANDRIEU C. On sequential Monte Carlo sampling methods for Bayesian filtering[M]. Kluwer Academic Publishers, 2000.
[5] 張琪, 胡昌華, 喬玉坤. 基于權(quán)值選擇的粒子濾波算法研究[J]. 控制與決策, 2008, 23(1):117-120.
[6] 夏飛, 郝碩濤, 張浩,等. 改進粒子濾波在汽輪機故障診斷中的應(yīng)用[J]. 計算機測量與控制, 2016, 24(1):35-38.
[7] ARORA S, SINGH S. Butterfly algorithm with Lèvy Flights for global optimization[C].International Conference on Signal Processing, Computing and Control. IEEE, 2016:220-224.
[8] GORDON N J, SALMOND D J, SMITH A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J]. IEE Proceedings F - Radar and Signal Processing, 2002, 140(2):107-113.
[9] DOUCET A, FREITAS N D, WAN E. The unscented particle filter[C]. Neural Information Processing Systems, NIPS, 2001: 584-590.
(收稿日期:2018-03-27)
作者簡介:
劉云濤(1991-),男,碩士,主要研究方向:嵌入式系統(tǒng)、人工智能。

