0  引言

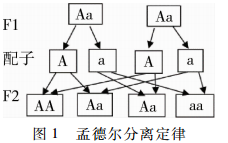
生物學(xué)中,，二倍體是指含有兩個同源基因組的個體^［1］,。根據(jù)孟德爾分離定律可知，當兩個同源基因組其中之一為顯性時,，該基因?qū)?yīng)的性狀表現(xiàn)為顯性,。僅當兩個同源基因組均為隱性時，表現(xiàn)型為隱性,，如圖1^［1］所示,。基因重組是保持生物特性世代遺傳的基本方式,，也是獲取大量遺傳變異的主要源泉,。遺傳算法^［2］中的交叉操作可視為對生物遺傳過程中基因重組的直接模擬,，交叉算子選擇得好壞直接影響算法的性能。對于占主流的二值編碼（0/1編碼）方法來說,，目前最常用的交叉方法主要有以下兩類：

（1）一點交叉,、兩點交叉與多點交叉^［1,3-4］

一點交叉（one-point crossover）又叫簡單交叉。具體操作是：在個體串中隨機設(shè)定一個交叉點,，實行交叉時,，該點前或后的兩個個體的部分結(jié)構(gòu)進行互換，并生成兩個新個體,。

兩點交叉（two-point crossover）方法與一點交叉類似,，只是多設(shè)置了1個交叉點，交叉時,，A,、B兩個體中位于這兩個交叉點之間的碼串相互交換，其余碼串不變,。

多點交叉(multi-point crossover) 是前述兩種交叉的推廣,，有時又被稱為廣義交叉（generalized crossover），一點交叉和兩點交叉可視為多點交叉的特殊形式,。

（2）一致交叉^［2］

所謂一致交叉（uniform crossover）是指通過設(shè)定屏蔽字（mask）來決定子個體的哪些基因繼承父本A 中的對應(yīng)基因,，哪些基因繼承父本B 中的對應(yīng)基因。一般來說,，點數(shù)較多的交叉操作可提供更加豐富的遺傳變異材料,，有利于維護種群基因型的多樣性，但對關(guān)鍵模式的保護能力較差,，收斂的速度也較慢,。從模式（schemata）處理角度看，一點,、兩點及多點交叉方法存在著“位置相關(guān)”的缺陷,。在此情況下，短模長模式比長模長模式有更大的存活概率,，而對于很多應(yīng)用問題,，因領(lǐng)域知識較少，基因間的關(guān)系密切程度不易確定,，人為的基因編碼排列方案可能極不合理,，這將影響多點交叉操作的效果和GA搜索的效率。

與多點交叉方法相比,，一致交叉由于平等對待所有的模式,，因而克服了多點交叉方法存在的“位置相關(guān)”缺陷，但在種群基因型相似性較高的情況下，由于隨機交換發(fā)生在相同基因座之間的概率較高,，故存在優(yōu)化后期階段進化遲鈍,、搜索效率欠佳的缺陷,。

針對上述問題,，參照生物DNA遺傳機制機理，提出并研究設(shè)計了一類擬合生物遺傳二倍體顯性機制的新型DNA遺傳算法,。

1  二倍體顯性遺傳算子

一點交叉,、多點交叉及一致交叉方法的共同之處在于均繼承了兩父串的相同基因，差異僅在于對父串不同基因的處理方式,。二倍體顯性遺傳算子也可以繼承親本同型等位基因,，而對雜型等位基因則按“與”和“或”邏輯分別進行處理。例如,，若兩父串為：

F1: 0100101101

F2: 1101110100

則由“與／或”交叉方法產(chǎn)生的兩子串分別為：

C1: 0100100100

C2: 1101111101

顯然,，這一遺傳操作方法使子代繼承了雙親的同型基因；對于雙親的雜型基因,，“與／或”交叉方法采取了兩種不同的“強調(diào)”策略：“與”運算強調(diào)0基因的作用,，而“或”運算則強調(diào)1基因 的作用。這種交叉方法較為逼真地模擬了生物DNA遺傳的顯性(dominance)機制,，“與”運算將1視為隱性基因,，而“或”運算將0視為隱性基因。

2  二倍體顯性遺傳計算模式分析

為便于對AO交叉方法進行模式分析,，這里參照Holland模式分析方法,，先定義幾個有關(guān)基因型模式的概念。

定義1： 0_模式由字符集{*0*}構(gòu)成的字符串稱作0_模式,，記為H0,。其中，字符0為反映模式結(jié)構(gòu)特征的確定性信息,，*為反映模式結(jié)構(gòu)特征的不確定性信息,。

定義2： 1_模式由字符集{*1*}構(gòu)成的字符串稱作1_模式，記為H1,。其中,，字符1為反映模式結(jié)構(gòu)特征的確定性信息，*為反映模式結(jié)構(gòu)特征的不確定性信息,。

有了這些定義,，再參考 Holland模式分析方法^［1,3-4］，不難得出二倍體顯性遺傳計算在模式形成和增長方面具有如下特性：

（1）1階優(yōu)模式的數(shù)目（數(shù)學(xué)期望）在連續(xù)后代中按式(1)增長：

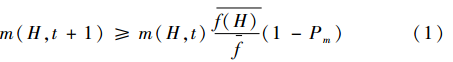
（2）高于種群的平均適應(yīng)度的1階0_模式在連續(xù)后代中按式(2)增長：

（3）高于種群的平均適應(yīng)度的1階1_模式在連續(xù)后代中按式(3)增長：

其中,，H表示某個模式,，m(H,t)表示在t代種群中隱含模式H的串的個數(shù)，m(H,t+1)表示在t+1代種群中隱含模式H的串的個數(shù)（數(shù)學(xu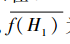é)期望），為t代種群中含模式H個體的平均適應(yīng)度,，f為t代種群中所有個體的平均適應(yīng)度,，Pm為變異概率，ο(H)為模式H的模階,。

很明顯,，與 Holland標準GA相比，基于二倍體顯性機制的DNA遺傳計算（AO交叉）對于適應(yīng)度高于種群平均適應(yīng)度的0_模式和1_模式有較強的保護能力,。而對于0,、1混雜的一般模式，AO交叉方法對模式H的破壞作用除了與變異概率以及模階的高低相關(guān)外,，還與模式H中的0和1個數(shù)之比相關(guān),。當模式H中0和1個數(shù)相等時，AO交叉對模式H的破壞作用最大,。

模式H中0和1在數(shù)目上相差越大,，AO交叉對模式H的破壞作用越小,；當模式H中的確定信息位全為0或全為1時,，AO交叉對模式H無破壞作用。由此不難推測AO交叉操作在搜索,、優(yōu)化應(yīng)用中可能具有如下特點：

（1）當問題全局最優(yōu)解的基因編碼為全0或全1時,，由于AO交叉對0_模式和1_模式無破壞作用，因此,，采用AO交叉的GA可能會以相當高的速度搜索到問題的全局最優(yōu)解,。

（2）當問題全局最優(yōu)解的基因編碼0、1個數(shù)在數(shù)量比上相差很大時,，由于AO交叉對這類0,、1混雜優(yōu)模式破壞作用較小，因此,，與一點交叉等方法相比,，采用AO交叉的GA可能會以相對較快的速度搜索到問題的全局最優(yōu)解。

（3）當問題全局最優(yōu)解的基因編碼0,、1個數(shù)在數(shù)量比上相差不大直至相等時,，由于AO交叉對這類0、1混雜優(yōu)模式破壞作用較大,，此時,，采用AO交叉的GA的收斂可能比較慢，甚至不及一點交叉或一致交叉等方法,。

3  遺傳優(yōu)化實驗

為了檢驗AO交叉方法的優(yōu)化性能,，本文選擇了易于采用 0/1二值編碼方案的典型優(yōu)化問題進行實驗,，即Bohachevsky函數(shù)優(yōu)化問題。

實驗環(huán)境為：Inter(R) Core(TM) i5-7300U CPU @2.6 GHz 2.71 GHz筆記本電腦,，Windows 10,，Visio Studio 2010。

Bohachevsky函數(shù)^［5-7］為：

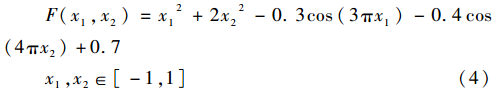
優(yōu)化目標為求Bohachevsky函數(shù)的全局最小值,。由數(shù)學(xué)分析方法可知Bohachevsky函數(shù)的最小值為0,，發(fā)生在(0,0)點。該函數(shù)三維形狀如圖2所示,。

實驗?zāi)康脑谟跈z測AO交叉方法的性能,，選用一點交叉作為比較對象，GA的配種選擇機制采用正比于適應(yīng)度的賭輪隨機選擇方式,。為了與AO交叉法的邏輯操作形式相一致，這里的變異操作采用“異或/異或非”方式,，其效果等同于位點變異方法,。實驗中的變異概率為0.05，交叉概率為1.00,，種群規(guī)模為400,，種群更新方式采用最佳保留方式。采用二進制編碼方式,，實驗結(jié)果如表1所示,，表中列出的優(yōu)化時間為20次實驗的平均值。

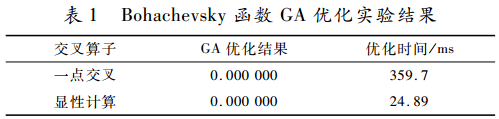
從實驗結(jié)果可以看出各種不同的交叉算子在Bohachevsky函數(shù)優(yōu)化中均能搜索到全局最優(yōu)解但優(yōu)化效率有差異,。AO 交叉操作方法在優(yōu)化效率方面明顯高于一點交叉方法,。根據(jù)前文對AO交叉方法的分析，AO交叉的優(yōu)化性能可能還與問題最優(yōu)解的編碼特性（0和1的數(shù)量比）相關(guān),。為此,，本文通過設(shè)置最小極值點發(fā)生的位置來改變?nèi)〉米顑?yōu)解時自變量編碼的0和1的個數(shù)。為檢測最優(yōu)解的編碼特性對AO交叉法優(yōu)化性能的影響,，令：

          x₁=y₁－m                      (5)

           x₂=y₂－m                      (6)

這樣,，如果針對自變量y1、y2進行遺傳優(yōu)化,，則Bohachevsky函數(shù)的最小極值點發(fā)生在(m,m),。實驗中，y1,、y2的編碼方式為二進制編碼方式,，位長均為30位。適應(yīng)度函數(shù)設(shè)計為：

           f（x₁,x₂）=1/（F（x₁,x₂）0.000 001）   (7)

為了調(diào)整最優(yōu)解的編碼特性,，本文將m線性映射到30位二進制編碼空間,，00…00對應(yīng)于 -1.00,11…11對應(yīng)于+1.00；實驗中的其他參數(shù)設(shè)計與前述Bohachevsky函數(shù)優(yōu)化相同。實驗結(jié)果表明,，采用AO交叉法的GA算法能搜索到Bohachevsky函數(shù)不同位置的全局最優(yōu)解,，但優(yōu)化所需時間有較大差異。圖3顯示了不同m值下,， AO交叉法的優(yōu)化時間曲線,，其中，縱坐標為優(yōu)化到最優(yōu)解所需的時間（20次實驗的平均值）,，橫軸為m在二進制編碼中所含0的個數(shù),，自0直到30。

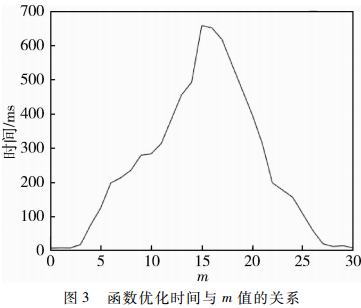
從圖3可以看出,，AO交叉方法的優(yōu)化效率隨著0,、1數(shù)目的變化有很大差異；在m值（二進制碼）為00…00和11…11時,，AO交叉方法的優(yōu)化效率最高,，而當m中的0、1個數(shù)比接近于1時,，AO交叉的優(yōu)化效率最低,。

4  結(jié)束語

與流行的一點交叉和一致交叉等方法相比，本文提出并研究設(shè)計的二倍體顯性DNA遺傳計算方法在模式抽樣機理方面有其獨特性,，主要表現(xiàn)在對優(yōu)質(zhì)0_模式和優(yōu)質(zhì)1_模式有較強的保護作用,。實驗結(jié)果顯示，這種抽樣特性導(dǎo)致AO交叉的優(yōu)化效率隨最優(yōu)解（二值編碼）的0,、1分布變化而發(fā)生變化,；最優(yōu)解包含的0和1的個數(shù)相差越大，則優(yōu)化效率越高,，反之,，則優(yōu)化效率越低。實驗結(jié)果也顯示出在最優(yōu)解包含的0和1的個數(shù)之比接近于1.00的較小范圍內(nèi),，AO交叉方法的優(yōu)化效率較低,。如果假定最優(yōu)解所包含的0（或1）個數(shù)呈均勻分布，則AO交叉方法將在總體優(yōu)化效率上明顯超越一點交叉等傳統(tǒng)遺傳算法,，統(tǒng)計實驗結(jié)果有力支持了上述理論分析與算法設(shè)計思想,。

需要特別指出的是，生物DNA遺傳過程除了多倍體顯性機制機理外,，還特別依賴于DNA雙螺旋結(jié)構(gòu),。生物DNA雙螺旋二倍體染色體結(jié)構(gòu)在群體遺傳基因多樣性維護方面有著獨特的功效。限于篇幅,，有關(guān)二倍體雙螺旋結(jié)構(gòu)的DNA模擬計算研究在此不做贅述,。

參考文獻

［1］ GLODBERG D E.Genetic algorithms in search, optimization & machine learning［M］.Addison-Wesley, Reading, Mass, 1989.

［2］ Peng Hu,Wu Zhijian,Zhou Xinyu, et al.Dynamic differential evolution algorithm based on elite local learning［J］.Acta Electronica Sinica,2014,，42 (8) : 1522-1530.

［3］ 魯宇明,黎明,李凌.一種具有演化規(guī)則的元胞遺傳算法［J］.電子學(xué)報,2010,38 (7) : 1603-1607.

［4］ 劉淵,楊永輝,張春瑞,等. 一種基于遺傳算法的Fuzzing測試用例生成新方法［J］.電子學(xué)報,2017,45(3):552-556.

［5］ FOGEL G, FOGEL D.Continous evolutionary programming:analysis and experiments［J］.Journal of Cybernetics and Systems,1994,26（1）:79-90.

［6］ 李柱.基于自適應(yīng)遺傳算法的軟件測試用例自動生成［J］.計算機系統(tǒng)應(yīng)用,2016,25(1):192-196

［7］ 陳賢富, 莊鎮(zhèn)泉,王煦法.遺傳算法的自適應(yīng)進化策略及TSP問題的遺傳優(yōu)化［J］. 電子學(xué)報, 1997,25 (7):111-114.

（收稿日期：2018-04-11）

作者簡介：

徐凱（1991-），女,，碩士研究生,，主要研究方向：深度學(xué)習(xí)與人工智能。

陳賢富（1963-）,，男,，副教授，主要研究方向：復(fù)雜系統(tǒng)與計算智能,。