0 引言

    近年來,，光伏發(fā)電(PV)在電力系統(tǒng)中的比例逐漸增加,，同時(shí)電動(dòng)汽車(EVs)也有逐漸取代內(nèi)燃機(jī)車(ICE)的趨勢，這些都導(dǎo)致了電力系統(tǒng)中存在不確定性因素^[1-2],。概率潮流（PLF）可用來評估包含上述不確定性因素的廣義電力系統(tǒng)的穩(wěn)態(tài)系統(tǒng)性能,。在PLF研究中，輸入隨機(jī)變量（RVs）的不確定性是概率模型,。PLF的根本任務(wù)是根據(jù)給定的輸入RVs的統(tǒng)計(jì)信息及其多重相關(guān)性,，表征結(jié)果變量（母線電壓和支路功率流）的概率分布^[3-4]。PLF評價(jià)的方法包括數(shù)值計(jì)算,、近似分析方法,。Monte-Carlo模擬（MCS）是PLF的一種數(shù)值計(jì)算方法，雖然計(jì)算準(zhǔn)確,，但是復(fù)雜度很高,，可以作為評價(jià)PLF算法精度的一種對比算法,?；诟唠A累積量的分析方法是一種有效的計(jì)算方法,，但是對于輸入RVs的過度依賴性，是具有挑戰(zhàn)性的因素^[5],。

    如今,，PLF的主要研究熱點(diǎn)是光伏發(fā)電不確定性對電力系統(tǒng)的影響分析，以及電動(dòng)汽車充電引起的不確定性對配電系統(tǒng)性能的影響^[6],。文獻(xiàn)[7]利用聯(lián)合累積量法分析了光伏發(fā)電高穿透率對輸電系統(tǒng)性能的影響,，PLF也適用于分析考慮光伏發(fā)電的配電系統(tǒng)。另一方面,，PLF用于研究考慮電動(dòng)汽車充電過程分析的文獻(xiàn)也很多,。文獻(xiàn)[8]中,，所有EV充電過程都是采用單一排隊(duì)模型來模擬的。文獻(xiàn)[9]中,，考慮了電動(dòng)汽車的每日到達(dá)時(shí)間,、發(fā)車時(shí)間和行駛距離，提出了電動(dòng)汽車充電模型,。文獻(xiàn)[10]中,，使用在交通管理局收集到的實(shí)時(shí)數(shù)據(jù)構(gòu)建了電動(dòng)汽車的充電模型，可以預(yù)測未來電動(dòng)汽車充電的數(shù)量,。文獻(xiàn)[11]中,，為了避免在高峰負(fù)荷時(shí)間充電，開發(fā)了一個(gè)基于使用時(shí)間的電動(dòng)汽車充電模型等,，此類文獻(xiàn)還有很多,，不再贅述。

    根據(jù)以上綜述可知,，沒有文獻(xiàn)綜合考慮光伏發(fā)電和電動(dòng)汽車充電需求的集成相關(guān)問題,，沒有考慮公共充電站和小區(qū)充電站充電速度問題，對于電網(wǎng)穩(wěn)定性的評價(jià)存在一定的片面性,。對此,，本文主要是針對上述兩個(gè)問題構(gòu)建考慮光伏發(fā)電和電動(dòng)汽車充電的PLF影響分析問題。分類考慮了插入式混合動(dòng)力電動(dòng)汽車（PHEV）和電池電動(dòng)車（BEV）充電問題,，并采用不同的排隊(duì)模型表征小區(qū)充電和公共充電站充電模型,。然后，采用基于Cornish-Fisher級數(shù)的擴(kuò)展累積估計(jì)方法對模型系統(tǒng)進(jìn)行估計(jì),。

1 概率潮流模型

1.1 輸電系統(tǒng)

    在電力系統(tǒng)中,，如果其由n條母線和1條分支線路構(gòu)成，則其線性PLF模型為：

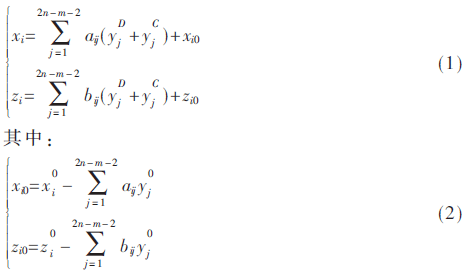
式(1)中,，x,、y和z分別是母線電壓、母線功率注入和線路功率流的矢量,；x⁰,、y⁰和z⁰分別是x,、y和z的期望值,；a_ij、b_ij是靈敏度系數(shù),；D和C分別代表該變量處于“離散”和“連續(xù)”狀態(tài),；x_i0、z_i0可以從確定性潮流中獲得,。

1.2 徑向分布系統(tǒng)

1.2.1 母線電壓幅值靈敏度矩陣計(jì)算

    考慮由n個(gè)母線組成的徑向分布系統(tǒng),，根母線的編號為0,，其余母線的編號依次為1，2,，…,，n-1，任意k母線的電壓幅值可表示為^[11]：

其中,，|V₀|表示根母線電壓的大?。沪V_k|表示從根母線到第k母線的總壓降,；P_i和Q_i分別為母線i上的有功和無功負(fù)載功率,；R_ik和X_ik分別表示從根母線開始到母線i和母線k的供電線路的總電阻和總電抗。式(3)的緊湊形式模型可以表示為：

其中,，K₁是母線電壓幅值靈敏度矩陣,，負(fù)載功率P和Q為RVs。

1.2.2 支路潮流靈敏度矩陣計(jì)算

    令徑向系統(tǒng)有l(wèi)個(gè)分支數(shù),，可通過兩步過程建立支路潮流靈敏度矩陣,。首先，假設(shè)系統(tǒng)是無損的,，無損支路潮流靈敏度矩陣K₂可利用母線負(fù)載函數(shù)進(jìn)行計(jì)算,。然后，支路損耗可表示為母線負(fù)荷功率函數(shù),，并可計(jì)算支路損耗靈敏度矩陣K₃,。最后，最后,，利用K₂和K₃的總和可獲得支路潮流的靈敏度矩陣K₄,。考慮到無損耗系統(tǒng),，任意支路i-j(母線i與母線j相連)的有功和無功支路功率流可表示為：

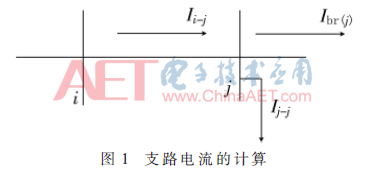
    根據(jù)式(8)~式(10),，可獲得式(7)的緊湊形式模型為：

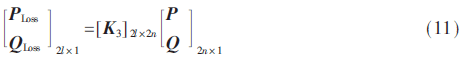
    最后，K₄可利用K₂和K₃計(jì)算得到,，即K₄=K₂+K₃,。

1.3 網(wǎng)格分布系統(tǒng)

    與徑向分布系統(tǒng)不同，在網(wǎng)格分布系統(tǒng)中無法直接獲得案例的靈敏度矩陣K₁和K₄,。首先,，通過在其中一個(gè)局部母線上斷開循環(huán)，可將網(wǎng)狀分布系統(tǒng)轉(zhuǎn)換為徑向分布系統(tǒng),。這會(huì)導(dǎo)致產(chǎn)生循環(huán)斷點(diǎn)(LBPs),，如圖2所示^[12]。

    圖2中，循環(huán)斷點(diǎn)j₁和j₂上的注入電流分別為I_ij和-I_ij,，其中I_ij是環(huán)路斷開前流經(jīng)母線j的電流,。則可利用類似徑向分布系統(tǒng)的計(jì)算過程獲得矩陣K₁和K₄的計(jì)算結(jié)果。

    為了計(jì)算LBP的注入電流,，可采用等效矩陣[Z_Th]方法,，LBP的功率注入過程如圖3所示。下面的迭代過程可以計(jì)算獲得注入電流矢量[I_t]的元素I_tj：

    (1)構(gòu)建等效矩陣[Z_Th],；

    (2)利用向前向后掃描迭代法,，計(jì)算LBPs兩端的電壓降，第一次迭代的電流的初始值設(shè)定為零,；

    (3)注入電流的增量計(jì)算形式為[ΔI_t]=[Z_Th]^-1[V_Th],，其中[V_Th]是LBPs兩端包含電壓降的矢量；

    (4)在任意的k步迭代中,，利用下式更新LBP電流注入：[I_t]^k=[I_t]^k-1+[ΔI_t]^k,。

    (5)重復(fù)執(zhí)行步驟(2)~步驟(4)，直到上述計(jì)算過程收斂,，收斂的閾值可設(shè)定為0.01 V,。

    同時(shí)，根據(jù)圖3所示過程,，令S_j為母線j上的復(fù)雜的功率需求,，在創(chuàng)建了循環(huán)斷點(diǎn)j₁和j₂后，循環(huán)斷點(diǎn)j₁和j₂上的復(fù)雜的功率需求計(jì)算形式為：

式中,，V_j1和V_j2分別為循環(huán)斷點(diǎn)j₁和j₂上電壓,。

2 考慮光伏發(fā)電和電動(dòng)汽車充電的不確定模型

2.1 光伏發(fā)電功率

    在光伏系統(tǒng)中，真正的光伏設(shè)備發(fā)電功率P_PV對于太陽輻照度具有較強(qiáng)的依賴性,，但是因?yàn)闅夂驐l件（云和霧）的不確定性,，導(dǎo)致其模型預(yù)測存在較大困難。根據(jù)文獻(xiàn)[10],，光伏設(shè)備發(fā)電功率P_PV可計(jì)算為：

2.2 電動(dòng)汽車功率需求

    目前,，有兩種類型的電動(dòng)汽車，第一種是由電池和ICE共同進(jìn)行供電的PHEV,，第二種是只由電池進(jìn)行供電的BEV,。在電動(dòng)汽車充電過程中，因?yàn)槊總€(gè)電動(dòng)車有不同的電池型號和容量,，因此它們的充電過程是不同的,，并具有時(shí)變特性。對于PHEV類型電動(dòng)汽車,，工作狀態(tài)可表示為：

其中,，Z是標(biāo)準(zhǔn)高斯RV。分布參數(shù)μ_m和σ_m分別是M_D自然對數(shù)的平均值和標(biāo)準(zhǔn)偏差值,，μ_m和σ_m分別與非對數(shù)平均值μ_md和標(biāo)準(zhǔn)偏差σ_md有關(guān)：

    利用排隊(duì)理論可得到BEV和PHEV的融合充電需求,。對充電站建立排隊(duì)模型M/M/C，其中,，第一個(gè)M表示客戶到達(dá)時(shí)間,，其滿足均值時(shí)間為T_λ的指數(shù)隊(duì)列。第二個(gè)M表示均值時(shí)間為T_μ的顧客服務(wù)時(shí)間,，C表示每次服務(wù)的最大客戶數(shù),。等待服務(wù)客戶數(shù)被認(rèn)為是無限的。在任何時(shí)刻客戶數(shù)量為n₁概率為：

其中,，U是均勻分布的RV,。電動(dòng)汽車需要在最小時(shí)間T_min內(nèi)完成充電。此外,，充電時(shí)間因?yàn)殡姵厝萘康南拗撇粦?yīng)超過最大時(shí)間T_max,。BEV中不考慮最大時(shí)間問題，因?yàn)槠湓试S完全充電,。由于充電站需要快速充電,，因此使用3級充電(400 V/63 A)。但是,，在小區(qū)充電情況下,，慢充電過程是可以接受的，可考慮1級充電過程(230 V/ 16 A),。充電電壓V和最大電流I_max是根據(jù)充電水平確定的,。電動(dòng)汽車的總充電需求可以計(jì)算為：

其中，I_i是第i個(gè)EV的充電電流,。

3 基于Cornish-Fisher擴(kuò)展累積估計(jì)

3.1 結(jié)果變量的累積量估計(jì)

    對于兩輸入情形,，兩個(gè)相關(guān)聯(lián)的EVs輸入X₁和X₂，其累積量計(jì)算公式為：

3.2 結(jié)果變量的近似概率分布

    使用Cornish-Fisher級數(shù)展開法（CFM）構(gòu)建結(jié)果變量的前五級近似概率分布,。利用Q標(biāo)準(zhǔn)與高斯分布分位數(shù)Q(q),，構(gòu)建變量Y的CFM近似結(jié)果累積概率圖，本文中選取q=1 000,。結(jié)果變量Y分量可以用式(39)和式(40)進(jìn)行近似：

3.3 計(jì)算過程

    為了獲得靈敏度矩陣模型的PLF,，MCS和ECM的計(jì)算程序如下：

    過程1：供電系統(tǒng)蒙特卡洛模擬

    (1)利用多項(xiàng)式正態(tài)變換技術(shù)按給定的相關(guān)系數(shù)矩陣獲得相關(guān)樣本輸入RVs的合并。

    (2)采用Newton-Raphson迭代法對每一組輸入RVs樣本集進(jìn)行模擬,，從而獲得結(jié)果變量的樣本輸出,。

    (3)結(jié)果變量的統(tǒng)計(jì)矩和概率分布可以從步驟(2)中獲得的樣本中建立。

    過程2：配電系統(tǒng)蒙特卡洛模擬

    (1)PHEVs和BEVs的瞬態(tài)充電數(shù)量,，對于公共充電站利用公式（26）隨機(jī)生成,，對于小區(qū)充電站利用公式（27）隨機(jī)生成,。然后，對于每種情形,，分別執(zhí)行步驟(2)~步驟(8),。

    (2)根據(jù)公共充電站和小區(qū)充電站的市場份額選取不同的PHEVs和BEVs參數(shù)。

    (3)對于PHEVs,，利用公式（18）生成P_EV和B_CAP的值,。對于BEVs，令P_EV=1,，則利用均值μ_CAP和方差σ_CAP的高斯分布函數(shù)隨機(jī)生成B_CAP,。如果B_CAP的計(jì)算值超出限定值則將其設(shè)定為其設(shè)定值邊界值。

    (4)利用公式（20）計(jì)算EV的每英里的能量消耗M_E,，利用公式（21）隨機(jī)生成EV每天行駛的英里數(shù)M_D,。

    (5)對于PHEV利用公式（24）計(jì)算每輛電動(dòng)車的每日充電量E_D，對于BEV,，每輛電動(dòng)車的每日充電量E_D=M_DM_E,。

    (6)利用公式（28）隨機(jī)生成充電時(shí)間T。

    (7)對于PHEV,，其中I_max和V取決于第3節(jié)所述的充電級別,。

    (8)利用公式（29）計(jì)算總的充電需求。

    (9)對于給定的相關(guān)系數(shù)矩陣,，輸入樣本RVs之間的相關(guān)性可采用多項(xiàng)式正變換技術(shù)獲得,。

    (10)通過前推回代迭代法模擬每一組輸入RVS樣品獲得樣品的結(jié)果變量輸出。

    (11)對于網(wǎng)格系統(tǒng)情形,，首先將系統(tǒng)轉(zhuǎn)換成徑向分布系統(tǒng),，見1.2節(jié)所述，然后執(zhí)行步驟(10),。

    (12)結(jié)果變量的統(tǒng)計(jì)矩和概率分布可以從步驟(10)和步驟(11)獲得的樣本中建立,。

    過程3：Cornish-Fisher級數(shù)擴(kuò)展累積估計(jì)

    (1)計(jì)算五級累積量：①隨機(jī)生成的EV負(fù)載需求，見過程1~2,；②其他輸入RVs,，例如光伏發(fā)電及其配電系統(tǒng)的融合總線負(fù)荷功率。

    (2)計(jì)算母線電壓和支路潮流靈敏度矩陣,。

    (3)利用步驟(2)和3.1節(jié)內(nèi)容計(jì)算結(jié)果變量的前五級累積量輸出,。

    (4)利用3.2節(jié)使用Cornish-Fisher級數(shù)展開法近似結(jié)果變量的累積概率圖。

4 實(shí)驗(yàn)分析

    本節(jié)中將分別在供電和配電系統(tǒng)中與MCS的性能進(jìn)行了比較,，同時(shí)考慮方案的準(zhǔn)確性和計(jì)算效率,，驗(yàn)證所提方法的有效性。

4.1 Ward Hale 6-bus供電系統(tǒng)測試

    Ward Hale 6-bus系統(tǒng)是由2個(gè)發(fā)電機(jī)組,、7條供電線路和2個(gè)變壓器分支電路構(gòu)成的簡單供電系統(tǒng)^[13-14],。集合(PV₁,，PV₂)和(PV₃，PV₄)分別代表光伏發(fā)電機(jī)組1和光伏發(fā)電機(jī)組2,。光伏發(fā)電機(jī)組線性化模型可利用式(15)表示,。

    考慮輸入RVs相關(guān)和不相關(guān)兩種情形，對于相關(guān)輸入RVs,，輸入RVs相關(guān)系數(shù)保持固定,。假定R₁,、R₂,、R₃和R₄四組RVs與T₁、T₂,、T₃和T₄四組RVs之間的固定相關(guān)系數(shù)為0.3,，其余的相關(guān)系數(shù)可構(gòu)成矩陣形式，如表1所示,。

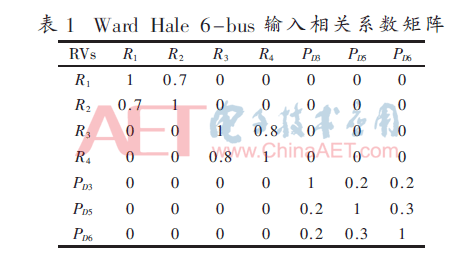
    對于不相關(guān)輸入RVs,，輸入RVs是不相關(guān)的，分別對光伏發(fā)電對結(jié)果變量的影響在基本情況下和光伏滲透情況下進(jìn)行研究,。絕對誤差百分比e_X作為誤差評價(jià)指標(biāo),，其中e_X=(e_μ+e_σ)/2，誤差均值e_μ和方差均值e_σ的具體計(jì)算形式為：

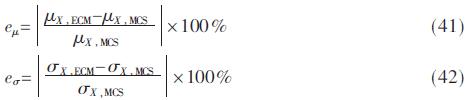
    圖4給出了系統(tǒng)在基本情況下（25%光伏滲透）和增加滲透后（50%光伏滲透）的概率密度累積量隨功率損耗的變化曲線,。

    根據(jù)圖4實(shí)驗(yàn)結(jié)果可知,，在基本情況下（25%光伏滲透）和增加滲透兩種系統(tǒng)中，其概率密度隨功率損耗的增加而增大,，但是總體上光伏滲透越小概率密度累積量越小,。

    由于恒定功率因數(shù)假設(shè)，總線3,、5和6的負(fù)載功率的有功和無功分量是完全相關(guān)的,。因?yàn)橄嚓P(guān)系數(shù)獨(dú)立于電網(wǎng)規(guī)模，Q_D3,、Q_D5和Q_D6的相關(guān)系數(shù)矩陣與表2設(shè)定相同,。在表2中比較了考慮輸入RVs相關(guān)和不相關(guān)兩種情形下使用該模型的有效性。

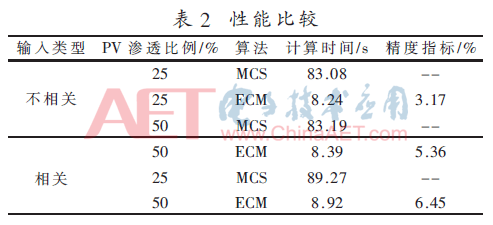
    根據(jù)表2實(shí)驗(yàn)結(jié)果可知,，在考慮輸入RVs相關(guān)和不相關(guān)兩種情形下,，在計(jì)算時(shí)間上，本文方法相對于蒙特卡洛方法具有明顯的優(yōu)勢,，本文方法計(jì)算時(shí)間保持在10 s以下,，而對比算法的計(jì)算時(shí)間在80 s以上。在精度指標(biāo)上,，因?yàn)槊商乜宀捎玫氖谴罅窟x取樣本點(diǎn)進(jìn)行模擬的方法,，因此其可近似于真實(shí)值,，本文將其作為參照，可見本文算法與蒙特卡洛方法在誤差上保持在7%以下,，體現(xiàn)了較高的精度性能,。

4.2 典型IEEE 140-bus配電模型測試

    本實(shí)驗(yàn)采用的實(shí)驗(yàn)?zāi)Ｐ腿鐖D5所示，利用圖5所示IEEE 140-bus配電模型^[15],，結(jié)合本文所提出的概率潮流計(jì)算模型進(jìn)行實(shí)驗(yàn)分析,，對比算法選取本文算法、三點(diǎn)估計(jì)和蒙特卡洛三種方法,。

    圖5所示的配電模型的總負(fù)荷是26.33+j18.61MV·A,；該配電模型的電源點(diǎn)有三個(gè)，分別位于標(biāo)號136,、123和107位置處,，其注入功率分別是6+j3.5MV·A，4+j2.5MV·A和7+j4.5MV·A,。配電模型的饋線電阻是r=0.27 Ω/km,，饋線電抗是x=0.327 Ω/km。

    這里以南京市玄武區(qū)2006年到2016年共10年間的氣候監(jiān)測數(shù)據(jù)作為模擬數(shù)據(jù)參數(shù),。以2013年為例,，選取四個(gè)具有季節(jié)特點(diǎn)的日期的檢測數(shù)據(jù)，時(shí)間點(diǎn)分別是1月15日,，4月22日,，8月9日，11月18日,，分別位于春夏秋冬四個(gè)季節(jié)中,，具體信息見表3所示。

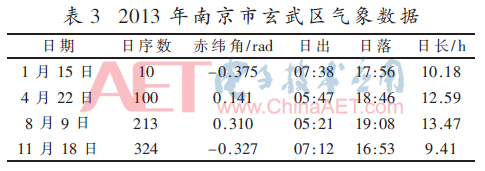
    表3中,，給出了南京市玄武區(qū)2013年一年中選取的四個(gè)時(shí)間節(jié)點(diǎn)的赤緯角,、日序數(shù)、日出日落兩個(gè)標(biāo)志性事件的時(shí)間,。IEEE 140-bus配電模型的發(fā)電設(shè)備位于節(jié)點(diǎn)99位置處,，該配電模型的峰瓦值參數(shù)取值是16 MW；該配電模型的覆蓋區(qū)域內(nèi)的PHEVs和BEVs的數(shù)量分別是2 900臺(tái)和600臺(tái),。電動(dòng)汽車進(jìn)行充電的節(jié)點(diǎn)位置是137節(jié)點(diǎn)處和113節(jié)點(diǎn)處,，分別是住宅區(qū)的慢充節(jié)點(diǎn)和公共區(qū)域的快充節(jié)點(diǎn)，電動(dòng)汽車在進(jìn)行充放電過程中的功率是3.7 kW,，這個(gè)過程中的能量轉(zhuǎn)換率是0.80,，功率因子參數(shù)的取值是0.98。圖6~圖7是采用三點(diǎn)估計(jì)法,、本文算法和蒙特卡洛模擬方法獲得的1月15日10：00~11：00時(shí)間段內(nèi)126節(jié)點(diǎn)和52節(jié)點(diǎn)的有功功率和電壓幅值兩個(gè)參數(shù)的概率密度,。在上述選取的四個(gè)時(shí)間點(diǎn)上,，本文方法和三點(diǎn)估計(jì)方法與蒙特卡洛方法相比在126節(jié)點(diǎn)和節(jié)點(diǎn)52的有功功率和電壓幅值的模擬誤差以及計(jì)算時(shí)間對比情況見表4結(jié)果所示。

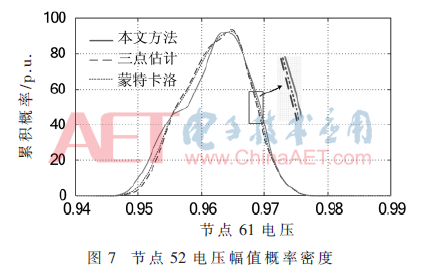
    分析上述圖6~圖7所示的有功功率和電壓幅值兩個(gè)參數(shù)的概率密度取值情況,，本文方法與蒙特卡洛方法獲得的線路126和節(jié)點(diǎn)52的有功功率和電壓幅值兩個(gè)參數(shù)的概率密度的偏差控制在5%以內(nèi),，而采用三點(diǎn)估計(jì)方法獲得的線路126和節(jié)點(diǎn)52的有功功率和電壓幅值兩個(gè)參數(shù)的概率密度的偏差在10%以內(nèi)。

5 結(jié)論

    現(xiàn)代社會(huì)中,，隨著經(jīng)濟(jì)和科技的快速發(fā)展,，新能源技術(shù)快速發(fā)展和應(yīng)用，針對這種發(fā)展背景,，本文研究了考慮包含光伏發(fā)電和電動(dòng)汽車充電的電力系統(tǒng)模型設(shè)計(jì)問題,。特別是，光伏發(fā)電和電動(dòng)汽車充電過程中存在的不確定性,、時(shí)變性,，通過理論分析得到了其概率潮流計(jì)算模型,，并采用不同的排隊(duì)模型表征小區(qū)充電和公共充電站充電模型,。然后，采用基于Cornish-Fisher級數(shù)的擴(kuò)展累積估計(jì)方法對模型系統(tǒng)進(jìn)行估計(jì),，實(shí)現(xiàn)了估計(jì)模型的降階處理,，提高了計(jì)算效率。實(shí)驗(yàn)結(jié)果顯示,，所提方法具有相對更高的計(jì)算精度和計(jì)算效率,。

參考文獻(xiàn)

[1] Dong Fugui，Zhang Wen.Evaluation and comparison of power network plans including distributed photovoltaic generations[J].Operational Research,，2017,，17(3)：885-900.

[2] LING J M，LIU P H.The performance analysis of photo-voltaic generation using the improved incremental conductance method under varying solar irradiance[J].Microsystem Technologies,，2018,，24(1)：235-241.

[3] 楊曉東，張有兵,，蔣楊昌,，等.微電網(wǎng)下考慮分布式電源消納的電動(dòng)汽車互動(dòng)響應(yīng)控制策略[J].電工技術(shù)學(xué)報(bào)，2018,，33(2)：390-400.

[4] JANIK P,，KOSOBUDZKI G，SCHWARZ H.Influence of increasing numbers of RE-inverters on the power quality in the distribution grids：a PQ case study of a representative wind turbine and photovoltaic system[J].Frontiers in Energy,，2017,，11(2)：155-167.

[5] Chen Weidong，Song Huan.Optimal subsidies for distributed photovoltaic generation: maximizing net policy benefits[J].Mitigation and Adaptation Strategies for Global Change,，2017,，22(3)：503-518.

[6] Dang Hongmei,，SINGH V P，GUDURU S,，et al.Nanotube photovoltaic configuration for enhancement of carrier generation and collection[J].Nano Research,，2015，8(10)：3186-3196.

[7] DAUD M Z,，MOHAMED A,，HANNAN M A.A novel coordinated control strategy considering power smoothing for a hybrid photovoltaic/battery energy storage system[J].Journal of Central South University，2016,，23(2)：394-404.

[8] 馬益平.考慮電動(dòng)汽車調(diào)度的微電網(wǎng)混合儲(chǔ)能容量優(yōu)化配置[J].電力系統(tǒng)保護(hù)與控制,，2017，45(23)：98-107.

[9] Wang Zhongkui,，PASSINO K M,，Wang Jin.Optimal reactive power allocation in large-scale grid-connected photovoltaic systems[J].Journal of Optimization Theory and Applications，2015,，167(2)：761-779.

[10] Qi Liqiang,，Zhang Yajuan.Effects of solar photovoltaic technology on the environment in China[J].Environmental Science and Pollution Research，2017,，24(28)：22133-22142.

[11] 徐從啟,，高瑞林，賈桂芝,，等.考慮分時(shí)電價(jià)電動(dòng)汽車負(fù)荷的微電網(wǎng)優(yōu)化調(diào)度[J].電氣工程學(xué)報(bào),，2017，12(11)：12-20.

[12] CORONA B,，ESCUDERO L,，QUEMERE G，et al.Energy and environmental life cycle assessment of a high concentration photovoltaic power plant in Morocco[J].The International Journal of Life Cycle Assessment,，2017,，22(3)：364-373.

[13] KHAN M J，MATHEW L.Different kinds of maximum power point tracking control method for photovoltaic systems：a review[J].Archives of Computational Methods in Engineering,，2017,，24(4)：855-867.

[14] PACHECO-TORRES R，LOPEZ-ALONSO M,，MARTINEZ G,，et al.Efficient design of residential buildings geometry to optimize photovoltaic energy generation and energy demand in a warm Mediterranean climate[J].Energy Efficiency，2015,，8(1)：65-84.

[15] Wang Jianjun,，Chen Shanben，Shao Yufeng.Research on maximum power point tracking in redundant load mode for photovoltaic system[J].Journal of Shanghai Jiaotong University (Science)，2016,，21(3)：257-262.

作者信息:

劉媛媛

（南京大學(xué) 新能源學(xué)院,，江蘇 南京210000）