文獻(xiàn)標(biāo)識碼: A
DOI:10.16157/j.issn.0258-7998.181228
中文引用格式: 王華華,陳東風(fēng),馬昶,等. 應(yīng)用于空間調(diào)制系統(tǒng)的低復(fù)雜度檢測算法[J].電子技術(shù)應(yīng)用,2019,45(1):60-63.
英文引用格式: Wang Huahua,Chen Dongfeng,Ma Chang,et al. Low complexity detection algorithm applied to spatial modulation system[J]. Application of Electronic Technique,2019,45(1):60-63.
0 引言
復(fù)雜的多條射頻鏈路與天線間同步技術(shù)應(yīng)用于大規(guī)模多輸入多輸出[1](Massive Multi-input Multi-output,Massive MIMO)系統(tǒng),導(dǎo)致系統(tǒng)的硬件實現(xiàn)難度大并且運算復(fù)雜度高。空間調(diào)制[2](Spatial Modulation,SM)技術(shù)是一種利用激活發(fā)送天線的序號和調(diào)制符號共同表示發(fā)送信息的新型傳輸方案,可完全消除空間多路MIMO系統(tǒng)中接收信號間的相互干擾,具有較高的傳輸速率,被認(rèn)為是一種新型的低復(fù)雜度與節(jié)能的多輸入多輸出(MIMO)傳輸方案,近年來受到業(yè)界的廣泛關(guān)注,關(guān)于SM[3]系統(tǒng)低復(fù)雜度的檢測算法相繼被提出。文獻(xiàn)[4]采用先對激活天線索引估計再對發(fā)送符號檢測。這種方案檢測性能較差,一旦天線索引檢測出錯則全部出錯。文獻(xiàn)[5]提出的是最大似然檢測算法,但由于ML算法窮舉遍歷所有可能的點,它的復(fù)雜度也非常高。文獻(xiàn)[6]提出的Tx-SD、Rx-SD兩種球形譯碼算法與最大似然檢測算法相比有近似最優(yōu)的性能并減少了檢測復(fù)雜度,但是不利于硬件實現(xiàn)。
為了平衡好復(fù)雜度和檢測性能之間的關(guān)系,本文將A-Star算法理論引入到信號檢測中。A-Star算法不僅考慮上一個路徑的成本還考慮未搜索子樹的估計成本。該算法減少了硬件訪問次數(shù),非常適合硬件實現(xiàn)。該檢測算法先將接收天線序列按度量值從大到小排序,再遍歷各子樹,這種方案將度量值小的節(jié)點排列到后幾層,能夠較早地排除有錯節(jié)點,使所選分支盡可能包括最優(yōu)路徑。提出的算法在減少復(fù)雜度的同時,還能保證A-Star算法近似最優(yōu)的檢測性能。
1 系統(tǒng)模型
假定發(fā)送天線為Nu根,接收天線為Nv根 通過準(zhǔn)靜態(tài)頻率平坦衰落信道進(jìn)行通信的多天線SM系統(tǒng)可以被建模為如圖1所示,SM的基本思想是將待發(fā)送的信息分為兩部分,一部分用于選擇激活發(fā)送天線的序號,另一部分用于選擇調(diào)制符號[7]。M是調(diào)制符號集合中元素總數(shù)大小,激活發(fā)送天線攜帶log2Nu個比特信息,調(diào)制符號攜帶log2M個比特信息,所以發(fā)送天線每次能有效地傳輸m=log2Nu+log2M個比特。lu表示激活發(fā)送天線的序號,并且lu∈{1,2,…,Nu},Su表示發(fā)送的調(diào)制符號,且Su∈{S1,S2,…,SM}。
通過準(zhǔn)靜態(tài)頻率平坦衰落信道進(jìn)行通信的多天線SM系統(tǒng)可以被建模為如圖1所示,SM的基本思想是將待發(fā)送的信息分為兩部分,一部分用于選擇激活發(fā)送天線的序號,另一部分用于選擇調(diào)制符號[7]。M是調(diào)制符號集合中元素總數(shù)大小,激活發(fā)送天線攜帶log2Nu個比特信息,調(diào)制符號攜帶log2M個比特信息,所以發(fā)送天線每次能有效地傳輸m=log2Nu+log2M個比特。lu表示激活發(fā)送天線的序號,并且lu∈{1,2,…,Nu},Su表示發(fā)送的調(diào)制符號,且Su∈{S1,S2,…,SM}。


2 A-Star算法
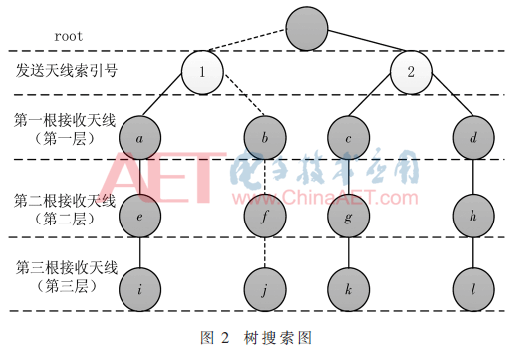
在A-Star算法樹搜索中,訪問節(jié)點(v,u)的順序通過啟發(fā)式函數(shù)k(u)確定。啟發(fā)式函數(shù)k(u)可分為初始節(jié)點到(v,u)節(jié)點實際路徑成本g(v,u)和從節(jié)點(v,u)到目標(biāo)成本函數(shù)h(v,u),即k(u)=g(v,u)+h(v,u)。接收天線數(shù)用Nv表示,樹搜索中的分支號為u,在樹搜索圖2中,u∈{1,2,3,4};層號用v表示,v∈{1,2,…,Nv}。
把A-Star算法應(yīng)用于根接收天線和根發(fā)送天線的空間調(diào)制系統(tǒng)中,結(jié)合式(3)得:


根節(jié)點與目前節(jié)點(v,u)的累積路徑成本表示為Pv,從式(5)開始P0=0,通過累積式(4)最終累積到PNr。圖2為2根收發(fā)天線、采用QPSK調(diào)制的SM系統(tǒng)通過A-Star算法的樹搜索過程圖。4種發(fā)送向量分別用圖2中的4個分支表示,當(dāng)前節(jié)點的部分歐幾里得距離(簡稱歐氏距離)用搜索樹中灰色圈的數(shù)值表示,搜索樹的根為A-Star算法初始節(jié)點。Pv等于初始節(jié)點到(v,u)節(jié)點的實際路徑成本g(v,u),h(v,u)為目標(biāo)成本。式(6)中a(v,u)代表當(dāng)前節(jié)點的成本av+1,l,是信道矩陣A的元素。

A-Star算法結(jié)合圖2從搜索樹第一層開始執(zhí)行以下步驟,具體過程如下:
(1)根據(jù)式(5),把P0初始化為0。
(2)根據(jù)式(4),計算出第一層中各個檢測點的累積成本值,令P1=g(1,u)。
(3)通過圖2可得出h(1,1)=e,h(1,2)=f,h(1,3)=g,h(1,4)=h;執(zhí)行啟發(fā)式函數(shù)k(u)=g(v,u)+h(v,u),則當(dāng)前隊列k(u)為k(1)=a+e,k(2)=b+f,k(3)=c+g,k(4)=d+h。
(4)通過比較k(u)判斷出此時最小的值,若此時最小點目標(biāo)成本值不等于0,則表明還沒到到葉子節(jié)點,所以需要繼續(xù)搜索。
(5)上一步確定了第一層最小節(jié)點,接著對最小節(jié)點的第二層的下一節(jié)點進(jìn)行搜索,并更新隊列k(u)。但是此時的最小點目標(biāo)成本值不為0,所以還需要繼續(xù)搜索。若此時最小點的值為0,該分支為最優(yōu)路徑,結(jié)束搜索。
3 分層排序A-Star算法
本文提出的分層排序A-Star算法先計算出接收天線索引的歐氏距離期望Er(r=1,2,…,Nv),然后對其進(jìn)行降序排列,使分支中節(jié)點度量值較小的點排到后幾層,這樣能排除有錯的節(jié)點,使所選分支盡可能包括最優(yōu)路徑,能夠極大縮小所需訪問節(jié)點數(shù)。期望Er可表示為如下公式:

式(7)只是運算了一根接收天線上的歐氏距離,再求M×Nu種情況的平均值。當(dāng)使用正交幅度調(diào)制或相移鍵控調(diào)制時,式(7)可表示為表達(dá)式(8)。

將各接收天線索引的歐氏距離期望值Er降序排列,然后把排序后的接收天線索引序列作為搜索層數(shù)序列,假設(shè)平均度量值排序為如圖3所示,畫出樹形搜索圖。結(jié)合A-Star算法對排序后的接收天線進(jìn)行樹搜索,找到最優(yōu)路徑。

4 復(fù)雜度和性能分析
4.1 復(fù)雜度分析
本文運算復(fù)雜度用算法過程中實數(shù)乘法運算數(shù)量來衡量。假設(shè)SM系統(tǒng)采用M階正交幅度調(diào)制方式,發(fā)送天線和接收天線分別為Nu根和Nv根。ML算法可能發(fā)射向量的總數(shù)是NuM, 需要6Nv次實乘,因此ML算法的計算復(fù)雜度C=6NuMNv[8]。A-Star算法計算第一層節(jié)點的g(l,u)和h(l,u)都需要6×Nu×M次實數(shù)乘法;若是除第一層之外所有層數(shù)的節(jié)點只需要考慮h(l,u),乘法次數(shù)為6×Nu×M×(Nv-2)。此外,因為并不是都能遍歷到所有節(jié)點,所以實際遍歷的復(fù)雜度為6×Nu×M×(Nv-2)。
需要6Nv次實乘,因此ML算法的計算復(fù)雜度C=6NuMNv[8]。A-Star算法計算第一層節(jié)點的g(l,u)和h(l,u)都需要6×Nu×M次實數(shù)乘法;若是除第一層之外所有層數(shù)的節(jié)點只需要考慮h(l,u),乘法次數(shù)為6×Nu×M×(Nv-2)。此外,因為并不是都能遍歷到所有節(jié)點,所以實際遍歷的復(fù)雜度為6×Nu×M×(Nv-2)。
本文提出的方案是在A-Star算法的基礎(chǔ)上增加了分層排序預(yù)處理過程, SM系統(tǒng)中式(7)在多進(jìn)制數(shù)字相位調(diào)制或多進(jìn)制正交幅度調(diào)制情況下,復(fù)雜度C=2Nv。當(dāng)每一幀有大量數(shù)據(jù)或信道慢衰落時,式(7)可以忽略計算復(fù)雜度,因此提出的檢測算法復(fù)雜度C≤2Nv+6NuM(Nv-2)。雖然本文算法添加了分層排序預(yù)處理過程,但是Nv的搜索空間降低了,復(fù)雜度中增加的2Nv與6NuM(Nv-2)的減少量相比是微不足道的,因此減少了所需訪問節(jié)點數(shù),與A-Star檢測算法相比復(fù)雜度降低了。
為了進(jìn)一步比較本文提出的算法與ML算法、TX_SD算法、RX_SD算法[9]和A-Star算法的計算復(fù)雜度,本文計算了SM系統(tǒng)在Nu=Nv=8、調(diào)制方式為64QAM時和在Nu=Nv=16、調(diào)制方式為32QAM時幾種不同算法的復(fù)雜度,其結(jié)果分別如圖4和圖5所示。


從圖4和圖5中可以看出,在SM系統(tǒng)中,ML檢測算法在所有情況下都是全搜索的,所以ML算法的計算復(fù)雜度極高。當(dāng)調(diào)制方式為64QAM、Nu=Nv=8時,本文算法的計算復(fù)雜度約為ML算法計算復(fù)雜度的4%,與TX_SD算法、RX_SD算法和A-Star算法相比分別降低了近55%、42%、20%。對比圖4和圖5仿真結(jié)果,發(fā)現(xiàn)接收天線數(shù)量增加時,本文提出的算法復(fù)雜度顯著降低。
4.2 性能分析
本節(jié)在不同參數(shù)下的SM系統(tǒng)中對本文的算法進(jìn)行仿真,在仿真中,信道模型均為瑞利衰落信道,噪聲為加性高斯白噪聲。圖6的仿真系統(tǒng)參數(shù)為Nu=Nv=8,4QAM、16QAM、64QAM調(diào)制。當(dāng)采用不同的調(diào)制方式時,系統(tǒng)的檢測性能明顯不同,性能最好的是4QAM,性能最差的是64QAM。

圖7仿真的系統(tǒng)參數(shù)為16QAM調(diào)制下,Nu=Nv分別取8、16和32。仿真結(jié)果表明,隨著天線數(shù)的增加,本文提出的算法都能獲得近似最優(yōu)的性能,同時表明隨著天線數(shù)的增加,系統(tǒng)性能也越好。

5 結(jié)論
在空間調(diào)制系統(tǒng)中,ML最優(yōu)檢測算法需要同時遍歷可能發(fā)送的調(diào)制符號組合和激活天線組合,計算復(fù)雜度較高,不利于硬件實現(xiàn)。針對此問題,本文提出了一種基于A-Star算法分層排序的低復(fù)雜度算法,首先對接受天線進(jìn)行分層并排序,然后根據(jù)排序結(jié)果改變樹搜索結(jié)構(gòu)并排除錯的節(jié)點,使所選分支盡可能包括最優(yōu)路徑。理論分析和仿真結(jié)果表明,該算法極大地縮小了接收端的搜索范圍,實現(xiàn)了計算復(fù)雜度與系統(tǒng)性能的優(yōu)化,具有較高的工程應(yīng)用價值。
參考文獻(xiàn)
[1] 王奔,張文彬,趙洪林.空間調(diào)制信號的低復(fù)雜度球形譯碼算法[J].哈爾濱工業(yè)大學(xué)學(xué)報,2017,49(5):22-30.
[2] XIAO L,YANG P,F(xiàn)AN S,et al.Low-complexity signal detection for large-scale quadrature spatial modulation systems[J].IEEE Communications Letters,2016,20(11):2173-2176.
[3] RENZO M D,HAAS H.Transmit-diversity for spatial modulation(SM):towards the design of high-rate spatially-modulated space-time block codes[C].IEEE International Conference on Communications.IEEE,2011:1-6.
[4] RAJASHEKAR R,HARI K V S,HANZO L.Antenna selection in spatial modulation systems[J].IEEE Communications Letters,2013,17(3):521-524.
[5] NTONTIN K,RENZO M D,PEREZ-NEIRA A,et al.Performance analysis of multistream Spatial Modulation with maximum-likelihood detection[C].Global Communications Conference.IEEE,2013:1590-1594.
[6] YEONG L H,WOONG P Y,MIN K J,et al.A low complexity sphere decoding algorithm based on double ordering for generalized spatial modulation[C].Symposium of the Korean Institute of Communications and Information Sciences,2016.
[7] NTONTIN K,RENZO M D,PEREZ-NEIRA A I,et al.A low-complexity method for antenna selection in spatial modulation systems[J].IEEE Communications Letters,2013,17(12):2312-2315.
[8] MEN H,JIN M.A low-complexity ML detection algorithm for spatial modulation systems with PSK constellation[J].IEEE Communications Letters,2014,18(8):1375-1378.
[9] WANG B,ZHANG W,ZHAO H,et al.Low complexity sphere decoding algorithm for spatial modulation signals[J].Journal of Harbin Institute of Technology,2017,49(5):22-30.
作者信息:
王華華,陳東風(fēng),馬 昶,亢 成
(重慶郵電大學(xué) 通信與信息工程學(xué)院,重慶400065)

