0 引言

    相對于模擬濾波器,，數(shù)字濾波器具有高精度、高可靠性,、可編程改變?yōu)V波特性,、便于集成等一系列優(yōu)點，并且理論上可實現(xiàn)近似理想頻率特性的濾波性能,。經(jīng)典的數(shù)字濾波器主要包括有限脈沖響應（Finite Impulse Response,，F(xiàn)IR）濾波器和無限脈沖響應（Infinite Impulse Response，IIR）濾波器,。相對于IIR濾波器來說,，當FIR濾波器系數(shù)保持線性對稱結構時，能夠在滿足幅頻響應要求的同時獲得嚴格的線性相位特性,。在數(shù)據(jù)通信,、語音信號處理、雷達信號處理等領域通常要求信號在傳輸過程中不能有明顯的相位失真,，因此FIR濾波器獲得了更廣泛的應用^[1],。

    FPGA因其獨特的可編程結構及強大的并行運算能力,，很適合于實現(xiàn)FIR濾波器設計?；贔PGA的FIR濾波器設計近年來一直是學者們研究的熱點,，主要集中在最優(yōu)濾波器設計方法、提高濾波器運行速度,、濾波器系數(shù)量化方法等方面^[2-7],。常規(guī)的系數(shù)量化方法僅關注對濾波器本身幅頻特性的影響^[8]，較少考慮在濾波器輸出位寬確定的情況下,，如何提高輸出幅度,，進而最大化輸出信噪比的問題。在研究分析傳統(tǒng)濾波器系數(shù)量化方法的基礎上,，提出了基于濾波器增益的系數(shù)量化方法,，給出了MATLAB及FPGA實現(xiàn)后的ModelSim仿真測試數(shù)據(jù)，結果表明這種方法最多可將濾波輸出幅度提高近一倍,，信噪比提高近6 dB,。

1 FIR濾波器原理及結構

    FIR濾波器，是指單位脈沖響應長度有限的濾波器,。FIR濾波器的突出特點是其單位取樣響應h(n)是一個N點長的有限長序列,，0≤n≤N-1。濾波器的輸出y(n)可表示為輸入序列x(n)與單位取樣響應h(n)的線性卷積,。

    從系統(tǒng)函數(shù)很容易看出,，F(xiàn)IR濾波器只在原點上存在極點，這使得FIR濾波器具有全局穩(wěn)定性,。FIR濾波器是由一個抽頭延遲線加法器和乘法器的集合構成的,，每一個乘法器的操作系數(shù)就是一個FIR系數(shù)。因此,，F(xiàn)IR的這種結構也被人們稱為抽頭延遲線結構,。圖1是FIR濾波器FPGA實現(xiàn)的典型結構圖。

2 系數(shù)量化對FIR濾波器性能的影響

2.1 FIR濾波器的MATLAB設計方法

    在采用FPGA編程實現(xiàn)FIR濾波器之前,，通常采用MATLAB軟件設計濾波器系數(shù),。MATLAB提供了豐富的FIR濾波器函數(shù)，分別對應不同的設計方法,，如窗函數(shù)法,、頻率取樣法、基于“最大誤差最小”的最優(yōu)設計法等,。為便于對比,，采用最優(yōu)設計方法設計FIR低通濾波器(MATLAB設計函數(shù)為firpm)，其參數(shù)為：采樣頻率32 MHz,，過渡帶0.5 MHz~1.5 MHz,。圖2為MATLAB設計出的濾波器幅頻響應圖,。

    由圖2可知，F(xiàn)IR濾波器的長度N越大,，濾波器過渡帶越接近設計參數(shù),，通帶及阻帶濾波性能越好，當N=41時阻帶衰減為26 dB,，當N=61時阻帶衰減為38.5 dB,，當N=81時阻帶衰減為48 dB；當系數(shù)長度超過一定值后（本實例為61）,，濾波器過渡帶的改善余量已很小,，但通帶及阻帶濾波性能會持續(xù)增加。不失一般性,，下文以長度為61的低通濾波器為例進行討論,。

2.2 系數(shù)的量化方法及其對濾波性能的影響分析

    根據(jù)MATLAB的FIR濾波器設計原理，無論濾波器長度多長,，濾波器通帶內(nèi)增益均為1（0 dB）,，濾波器系數(shù)為帶小數(shù)的浮點數(shù)。由于FPGA只能處理二進制數(shù)據(jù),，MATLAB設計出的濾波器系數(shù)需要轉換成二進制數(shù)據(jù)才能完成FPGA電路實現(xiàn),。

    濾波器系數(shù)是帶符號的數(shù)據(jù),，F(xiàn)PGA實現(xiàn)時需要用二進制補碼格式表示,。設濾波器系數(shù)的量化位寬為Q，則系數(shù)C的表示范圍為-2^Q-1≤C≤(2^Q-1-1),，又由于FIR濾波器系數(shù)的嚴格對稱特性,，實際范圍為(1-2^Q-1)≤C≤(2^Q-1-1)。

    傳統(tǒng)的濾波器系數(shù)量化方法可分解為3個步驟：(1)找出濾波器系數(shù)中最大的絕對值數(shù)M,；(2)以M為基準,，對所有濾波系數(shù)進行歸一化處理，即對所有系數(shù)除以M,；(3)對所有濾波器系數(shù)乘以(2^Q-1-1),，并對處理后的系數(shù)取整形成整數(shù)系數(shù)；(4)將整數(shù)濾波器系數(shù)轉換成二進制補碼數(shù)據(jù),。圖3為不同量化位寬情況下的濾波器幅頻響應圖,。

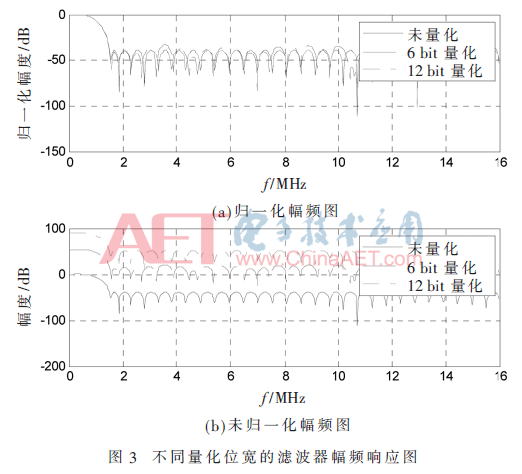
    由圖3(a)中的歸一化幅頻圖可知，濾波器系數(shù)量化位寬越小,，量化后的濾波性能越差(當量化位寬為6 bit時,，阻帶衰減相比量化前減小了約6 dB)，反之量化位寬越大,，量化前后的濾波性能相差越小,。當量化位寬超過一定值(本實例為12 bit)后,，濾波性能幾乎不再變化。不失一般性,，下文以長度為61,、量化位寬為12 bit的低通濾波器為例進行討論。

3 基于增益的FIR濾波器系數(shù)量化方法

3.1 一般量化方法對系統(tǒng)性能的影響

    根據(jù)前面討論的濾波器量化方法,，系數(shù)量化過程相當于濾波器增益擴大了(2^Q-1-1)/M倍,。從圖3(b)中的未歸一化幅頻圖可知，量化位寬越大,，濾波器通帶內(nèi)的增益越大,。當量化位寬為6 bit時，通帶增益為54 dB,，當量化位寬為12 bit時,，增益為90 dB。

    FPGA設計FIR濾波器,，一般采用定點二進制數(shù)據(jù)進行運算,。前面討論系數(shù)量化對系統(tǒng)性能的影響時，實際有一個前提條件,，即濾波運算采用全精度運算,，濾波運算的結果保留全部有效數(shù)據(jù)位。當濾波器系數(shù)量化位寬為Q時,，由于濾波器增益擴大了(2^Q-1-1)/M倍（一般來說,，M≤1），為保證全精度運算,，保留全部有效濾波輸出位寬,，相對于濾波器輸入信號而言，位寬將增加Q_a bit,。其中

    對于前面討論的長度N=61,，量化位寬Q=12的低通濾波器而言，M=0.062 1,，(2^Q-1-1)/M=32 963,，則濾波輸出位寬需增加Q_a=16 bit。假設輸入數(shù)據(jù)位寬為10 bit,，則濾波器全精度輸出位寬為26 bit,。

3.2 基于增益的系數(shù)量化方法

    根據(jù)前面的討論，量化濾波器系數(shù)后,，輸出有效位寬所能表示信號的信噪比下降,，是由于濾波輸出信號達不到滿量程狀態(tài)。為此,，優(yōu)化濾波器系數(shù)量化方法,，采用基于濾波器增益的方法對系數(shù)進行量化,。結合前述的濾波器實例，具體步驟為：(1)對所有濾波器系數(shù)乘以=2¹⁶=65 536,，并對處理后的系數(shù)取整形成整數(shù)系數(shù),；(2)將整數(shù)濾波器系數(shù)轉換成二進制補碼數(shù)據(jù)。

    經(jīng)過改進的量化處理后,，相當于對濾波增益直接增加了65 536倍（常規(guī)方法僅增加了32 963倍）,，濾波輸出的數(shù)據(jù)幅值能夠達到輸出數(shù)據(jù)有效位寬所能表示的滿量程值，實現(xiàn)了輸出位寬一定的條件下,，輸出信號信噪比的最大化,。經(jīng)過這樣的量化處理，系數(shù)的量化位寬為：

    對于上文所討論的低通濾波器,，量化位寬需要13 bit,。圖4為常規(guī)量化方法和改進量化方法的濾波器系數(shù)（沖激響應）圖，其中Q_a=16,。

    從圖4可以看出,，在濾波輸出位寬相同的條件下，改進的量化方法所產(chǎn)生的濾波器系數(shù)（沖激響應）幅值大于常規(guī)方法,，相當于濾波器增益更大,。同時也要注意到，改進的量化方法所需的濾波器系數(shù)位寬由12 bit增加到13 bit,。也就是說,，增加濾波器增益，是以增加系數(shù)量化位寬為代價的,。

4 FPGA實現(xiàn)后的測試結果分析

    接下來采用Xilinx的Spartan6系列FPGA器件XC6SLX25-FT256C為目標平臺,，調(diào)用ISE14.7工具中的FIR濾波器核,，實現(xiàn)前文所討論的低通濾波器(采樣頻率為32 MHz,，過渡帶為0.5 MHz~1.5 MHz，濾波器長度N=61),。仿真工具為ModelSim10.1,，輸入信號為2路單頻信號的疊加。兩路單頻信號頻率分別為0.22 MHz和2 MHz,，功率比為1:1,。輸入位寬為10 bit，濾波器輸出位寬為26(Q_a=16),。圖5,、圖6分別為常規(guī)量化方法和改進量化方法的濾波器ModelSim仿真波形圖。

    從圖5,、圖6中可以看出,，兩種方法都能夠有效濾除帶外干擾信號（2 MHz單頻信號）,，改進量化方法的濾波器輸出信號幅度值（16，641,，407）明顯大于常規(guī)量化方法的幅度值（7,，910，390）,，相當于增加了濾波增益,，增加了濾波輸出信號的信噪比。

5 結論

    本文詳細分析了濾波器系數(shù)量化方法對濾波性能的影響,。在對常規(guī)系數(shù)量化方法的步驟,、原理進行分析的基礎上，針對濾波輸出數(shù)據(jù)幅值達不到有效位寬滿量程的現(xiàn)象,，提出了基于濾波器增益的系數(shù)量化改進方法,。MATLAB仿真及FPGA實現(xiàn)后的ModelSim仿真均表明，在濾波輸出位寬相同的條件下,，改進的量化方法可以有效提高濾波器增益,，進而提高濾波輸出信號的信噪比。需要注意的是,，增加濾波器增益是以增加系數(shù)量化位寬,、增加FPGA實現(xiàn)后的邏輯資源為代價的。

參考文獻

[1] 高耀鴻.基于FPGA的FIR低通濾波器[D].長沙：湖南大學,，2012.

[2] 朱效效,，蔡俊，陸偉.基于優(yōu)化DA算法濾波器的設計及其FPGA實現(xiàn)[J].電子技術應用,，2015,，41(2)：59-60，64.

[3] 徐彥凱,，雙凱.提高定點精度的FPGA信號處理算法[J].計算機工程與科學,，2012，34(9)：197-200.

[4] 郭廣浩,，劉志哲,，孟慶龍，等.多級并行流水FIR數(shù)字濾波器的設計與驗證[J].現(xiàn)代電子技術,，2015,，38(1)：69-72.

[5] 李凱勇.基于FPGA高效FIR濾波器設計[J].青海大學學報，2017,，35(6)：56-60.

[6] 張娜,，李春祎.多相并行FIR濾波器的FPGA高速實現(xiàn)方法[J].無線電通信技術，2017，43(4)：86-90.

[7] 周龍,，王紅玲,，崔新瑩，等.基于FPGA及分布式算法濾波器[J].電子設計工程,，2017,，25(23)：139-142.

[8] 曹振吉，何敏.基于FPGA和Matlab的FIR數(shù)字濾波器[J].現(xiàn)代電子技術,，2015,，38(19)：98-101.

作者信息:

杜  勇

（四川工商學院 電子信息工程學院，四川 成都611745）