0 引言

    預測資產(chǎn)的未來價格一直以來都是個人投資者和機構(gòu)投資者的重要問題。其中,，股票價格的預測是非常困難的,，因為股票市場是不確定的、非線性的復雜動態(tài)系統(tǒng),，而且受眾多因素影響,。對于專業(yè)交易員，基本面分析和技術(shù)分析是最常見的兩種交易決策方式,?；久娣治鲋饕怯煤暧^的經(jīng)濟、工業(yè)和商業(yè)指標,。技術(shù)分析主要是使用歷史價格數(shù)據(jù)和相關(guān)的技術(shù)指標,，事實上是假設原先的價格會對以后的價格有影響。

    從歷史時間序列來預測價格與FAMA E F的有效市場假說^[1]違背,。按照這一假說,，有效市場無法從歷史價格中預測未來價格。但事實上,，有很多研究與這一假設是相違背的,，特別是基于技術(shù)分析的研究。在股票市場上，技術(shù)分析主要運用的方法可以簡單分為統(tǒng)計和人工智能（機器學習）兩大類,。通常價格的時間序列天然具有無序,、有噪聲、非線性等特性,，不是一個固定的形態(tài)^[2],。因此，統(tǒng)計方法在股票指數(shù)的預測上表現(xiàn)不佳,，本文決定使用機器學習方法來對股指價格進行預測,。

    以往研究中，單個KNN模型難以滿足預測股票價格的需要,，混合模型和改進模型更為常見,。Li Hui等按照K近鄰的思路來對財務困境特別是破產(chǎn)預警問題進行預測^[3]。TEIXEIRA L A和OLIVEIRA A L I結(jié)合K近鄰和常用的技術(shù)分析工具進行實證,，認為預測短期股票價格趨勢是可行的^[4],。趙俊杰利用ReliefF算法確定特征的權(quán)值，對K最近鄰特征投影算法進行改進^[5],。NAYAK R K等提出了一個支持向量機和K近鄰混合的模型預測印度股票指數(shù),。比較其他模型，他們認為這一模型能夠很好地利用高維數(shù)據(jù),、有更好的預測能力^[6],。Chen Yingjun和Hao Yongtao提出了一個基于特征的加權(quán)支持向量機和加權(quán)的K近鄰混合模型。權(quán)重通過計算信息增益來確定,，在上證綜指和深證綜指上進行實證,，具有不錯的預測表現(xiàn)^[7]。集成模型在股票價格預測研究中也十分常見,。PATEL J等比較了神經(jīng)網(wǎng)絡(ANN),、支持向量機(SVM)、隨機森林(RF),、樸素貝葉斯(NB),，隨機森林有更好的預測表現(xiàn)^[8]。隨后,，PATEL J等混合了ANN模型,、RF模型、SVR模型,，其中VR-ANN模型有著最好的整體表現(xiàn)^[9],。Zhang Xiaodan等將AdaBoost算法與概率支持向量機結(jié)合，成功地解決了轉(zhuǎn)折點的不均衡問題^[10],。

    本文希望利用技術(shù)指標有效地對股票指數(shù)進行預測,。K近鄰(K-Nearest Neighbor,，KNN)算法利用預測數(shù)據(jù)最接近的訓練數(shù)據(jù)進行預測。盡管這不能實現(xiàn)對價格運動的解釋,，但有很好的經(jīng)濟學含義,，即過去發(fā)生的價格運動與現(xiàn)在的價格運動在特征上是相似的。本文使用K近鄰算法對股票價格的運動模式進行識別和預測,，解決投資交易中的擇時問題,；隨后使用滑窗方法,，比較不同歷史數(shù)據(jù)的相似情況,；最后使用多個K近鄰模型構(gòu)成一個投票的集成模型，增強模型的預測能力和泛化能力,。

1 實驗原理

1.1 K近鄰模型

    K近鄰學習是機器學習中一種常見的監(jiān)督學習方法,，其工作機制非常簡單。在給定訓練樣本后,，基于某種度量找出訓練集與測試集中最接近的K個樣本,，即所謂的K個鄰居來預測樣本類別。度量通常使用標準歐幾里德距離,。預測通常使用“投票法”,，選擇K個樣本中最多的類別作為預測結(jié)果。顯然K是一個很重要的參數(shù),，會對分類結(jié)果產(chǎn)生重要的影響,。本文基于這樣的假設：在股票市場上，過去發(fā)生過的情況仍會發(fā)生,，股票價格運動在特征上是相似的,。預測前，使用交叉驗證來確定訓練數(shù)據(jù)中最優(yōu)參數(shù)K,。K近鄰雖然簡單,，但其預測能力不可小覷。當給定測試樣本x,，其最近鄰樣本為z,，則最近鄰分類器出錯概率，即x與z類別標記不同的概率為：

1.2 集成模型

    集成學習是結(jié)合使用給定學習算法的幾個基本估計器的預測,，以便通過單個估計器來提高模型的泛化能力,。其中，bagging是常見的一類方法,，其建立在原有訓練集的隨機子集黑匣子估計的幾個基礎(chǔ)學習器,，然后匯總它們各自的預測，形成最終的預測算法,。這類方法減少基本估計量方差,，將隨機化引入到其構(gòu)建過程中,，最后合并出來。在許多情況下,，bagging構(gòu)成了一種非常簡單的改進單一模型的方式,，而不需要適應基礎(chǔ)的基本算法。Boosting是另一種將弱學習器提升為強學習器的算法：先從訓練集中訓練出一個基礎(chǔ)學習器,，在根據(jù)其表現(xiàn)對樣本分布進行調(diào)整,，基礎(chǔ)學習器中錯誤的訓練樣本受到更多關(guān)注，進行調(diào)整來訓練下一個基礎(chǔ)學習器,，循環(huán)往復,，直到基礎(chǔ)學習器數(shù)量達到最初設定的值t。最后將t個基礎(chǔ)學習器進行加權(quán)結(jié)合,。

    為了增強預測能力,，本文使用多個K近鄰分類器組成一個集成分類器，在單個K近鄰模型的分類投票后進行再次投票,。由于K近鄰分類中參數(shù)K對結(jié)果影響重大,，本文將使用不同參數(shù)K的K近鄰分類器來組成一個集成分類器。盡管訓練數(shù)據(jù)的最優(yōu)K值未必是預測數(shù)據(jù)中最優(yōu)的,，但假設這一K值也是十分接近最優(yōu)值的,，只是不能準確地知道確切值。使用訓練數(shù)據(jù)中最優(yōu)K值的鄰域構(gòu)建多個K近鄰模型,。最后進行投票,，與單個K近鄰模型的分類投票原則“少數(shù)服從多數(shù)”不同，使用“一票否決”增加了預測的準確度,，避免錯誤交易和不必要交易帶來的損失,。

2 預測仿真

2.1 數(shù)據(jù)情況

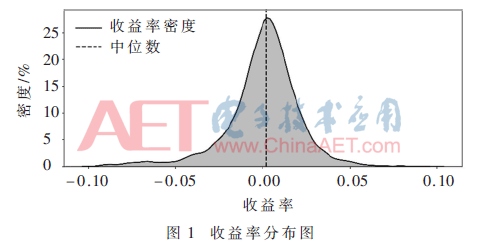
    本文使用中證500指數(shù)(CSI500)的價格數(shù)據(jù)，時間從2007年～2018年9月,，數(shù)據(jù)包括收盤價,、開盤價、最高價,、最低價,、5日均價（收盤價）、成交額和漲跌額,。數(shù)據(jù)均來Wind金融終端,。這些都是常用數(shù)據(jù)，不存在缺失項問題,，所有數(shù)據(jù)進行統(tǒng)一的標準化處理,。對價格運動進行簡單劃分，按照收益率將所有交易日劃分為漲和跌兩種模式,。與絕大多數(shù)之前研究不同,，本文不以0收益率為劃分界限,，按照中位數(shù)（50%分位數(shù)）進行劃分，前50%標記為類別‘1’（漲）,，后50%標記為類別‘0’（跌）,。

    在圖1中，可以看到中證500指數(shù)的收益分布大致對稱,，中位數(shù)與0十分接近,。通過上面的類別劃分，可以得到兩類數(shù)量相當?shù)挠柧殧?shù)據(jù),，避免了類別不平衡問題,。

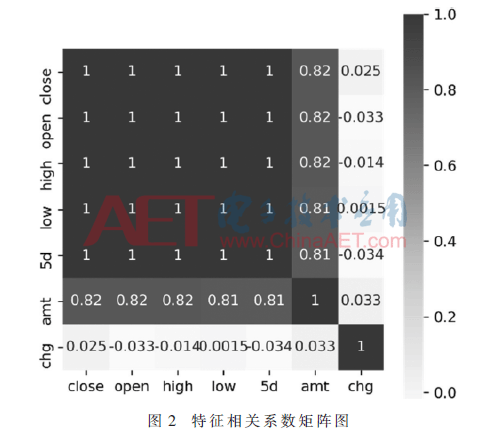
    觀察圖2中特征間的相關(guān)系數(shù)，可以看到價格的收盤價（close）,、開盤價(open),、最高價(high)、最低價(low)和5日均價(5d)有非常強的線性相關(guān),，成交額(amt)也與價格指標有很強的正線性相關(guān)，但漲跌額(chg)與其他指標的相關(guān)系數(shù)很小,，可以認為漲跌與其他指標不存在線性相關(guān)性,。考慮相關(guān)系數(shù),，為了盡可能地減少數(shù)據(jù)特征和保留完整的經(jīng)濟學意義,，本文只使用最高價（high）、最低價（close）,、五日均價（5d）,、成交額（amt）和漲跌額（chg）5個特征。

    考慮實際交易具有可操作性,，所有特征進行滯后一天處理,，即用前一天的數(shù)據(jù)預測下一天的漲跌。在操作上,，本文假設允許進行雙向操作,，預測為漲的交易日做多，預測為跌的交易日做空,。由于漲跌模式的變化通常比較頻繁,，因此考慮了手續(xù)費對收益的影響，每次交易收取千分之1.5的費用,。

2.2 K近鄰模型預測

    將2007年～2016年的數(shù)據(jù)作為訓練數(shù)據(jù),，2017年～2018年9月的數(shù)據(jù)作為預測數(shù)據(jù)。首先使用單個K近鄰模型進行中證500指數(shù)的漲跌預測,。由于K近鄰模型中,，參數(shù)K的作用十分重要,，本文使用網(wǎng)格搜索，使其在訓練數(shù)據(jù)中最優(yōu),，得到K=17是訓練數(shù)據(jù)的最優(yōu)參數(shù),，隨后對預測數(shù)據(jù)進行預測。單個KNN策略的收益情況如下,，由于參考K=17,，將此策略簡稱為K17KNN，該策略考慮手續(xù)費簡稱為K17KNN_fee,，收益表現(xiàn)如圖3所示,。

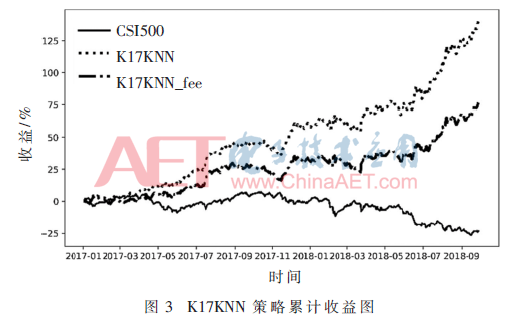
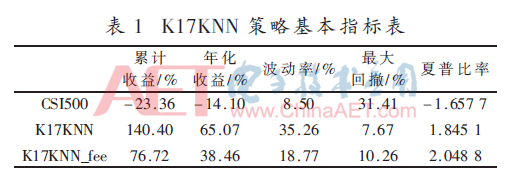
    在表1中，預測的21個月中,，單個KNN模型獲取140.40%的收益,，扣除手續(xù)費仍然有76.72%的收益。手續(xù)費對收益情況有相當大的影響,。觀察波動率,、最大回撤和夏普比率，看到單個KNN模型通過參數(shù)K調(diào)優(yōu)可以獲得一個不錯的交易結(jié)果,。

2.3 滑窗方法預測

    K近鄰是一種懶惰算法,，基本沒有訓練模型的過程。這意味著預測結(jié)果嚴重依賴于訓練數(shù)據(jù)的質(zhì)量,。K近鄰模型有著十分強烈的內(nèi)在含義,，即預測樣本與哪些訓練樣本在特征上更接近（相似）。使用這一模型可以解答一個有趣的問題,，現(xiàn)在股票價格的運動與遙遠的歷史更接近還是與剛剛的過去更接近,。理論上，對現(xiàn)在的股票價格運動而言,，遙遠的過去可能有更接近的價格表現(xiàn),，剛剛的過去則有基本一致的宏觀背景。

    在K近鄰模型下,，調(diào)整訓練數(shù)據(jù),，觀察預測結(jié)果來回答這一問題。使用滑窗方法來調(diào)整訓練數(shù)據(jù),，較短的窗口代表剛剛的過去,，較長的窗口來代表遙遠的歷史。利用不同訓練數(shù)據(jù)的收益差別,，觀察模型的預測差別,，即數(shù)據(jù)間相似情況的差別。

    在圖4～圖6中,，return代表策略的累計收益,，return_fee代表策略考慮手續(xù)費后的累計收益,。使用不同長度窗口的滑窗KNN模型，對2017年～2018年9月進行預測,，不同窗口長度的KNN模型之間預測效果差異很大,。整體而言，窗口越長策略收益越好,。也就是說,，現(xiàn)在股票價格與遙遠的歷史數(shù)據(jù)更接近，而不是剛剛過去的數(shù)據(jù),。

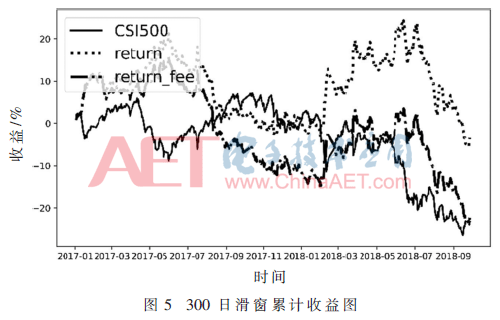
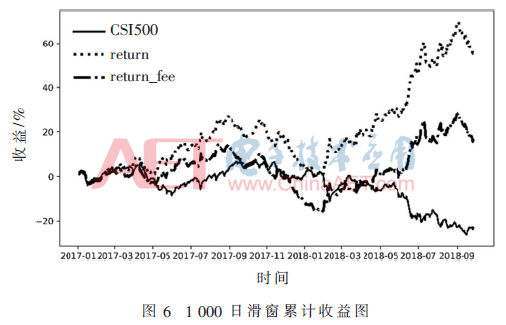
2.4 集成模型預測

    前面的單個K近鄰模型已經(jīng)能夠?qū)崿F(xiàn)不錯的股票漲跌模式預測,。但事實上，訓練數(shù)據(jù)的最優(yōu)K值未必是預測數(shù)據(jù)的最優(yōu)K值,，單個K近鄰模型的表現(xiàn)未必穩(wěn)定,。為了進一步增強K近鄰的預測能力和泛化能力，本文使用多個K近鄰模型組成一個集成學習模型,，也可以稱為集成學習器,。

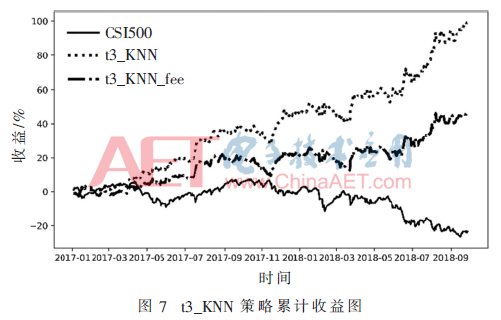
    除了訓練數(shù)據(jù)的最優(yōu)參數(shù)K=17，本文還使用17的鄰域16和18來構(gòu)建一個基于3個基礎(chǔ)學習器的集成學習器,。當3個學習器的預測均為漲時,，做多；當3個學習器的預測均為跌時,，做空；其他情況不操作,。由于使用了3個KNN模型,，即t=3，將此集成模型策略簡稱為t3_KNN,，該策略考慮手續(xù)費簡稱為t3_KNN_fee,，收益表現(xiàn)見圖7。在表2中,，t3集成模型與之前的單一模型對比,，最大回撤和夏普比率基本相當，波動率得到有效減少,，但其代價是收益率的下降,。

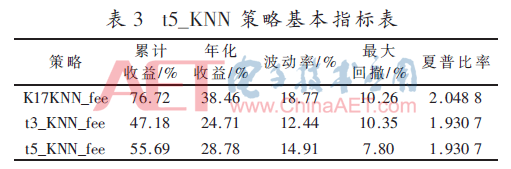
    進一步增加基礎(chǔ)學習器的數(shù)量，使用K=15,、16,、17、18,、19 5個基礎(chǔ)學習器（即t=5）構(gòu)成集成學習器進行預測,。同樣,，此策略簡稱為t5_KNN，考慮手續(xù)費簡稱為t5_KNN_fee,，收益表現(xiàn)見圖8,。在表3中，t5集成模型與t3集成模型相比,，夏普比率相當,，增加了收益和降低最大回撤，增加了一定的波動率,。

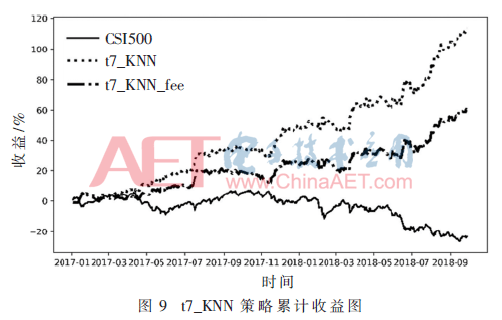
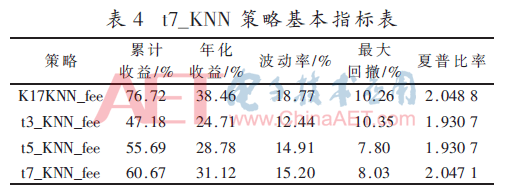
        進一步增加基礎(chǔ)學習器的數(shù)量,，使用K=14、15,、16,、17、18,、19,、20共7個基礎(chǔ)學習器構(gòu)成集成學習器進行預測。同樣,，此策略簡稱為t7_KNN,，考慮手續(xù)費簡稱為t7_KNN_fee，收益表現(xiàn)見圖9,。在表4中,，t7集成器與t5集成器相比，夏普比率,、最大回撤和波動率相當,，但收益得到進一步提升?？梢赃M一步增加基礎(chǔ)學習器的數(shù)量,，但收益表現(xiàn)并非隨著數(shù)量的增加而提高。以上的集成器與單個模型相比,，是以收益為代價來降低最大回撤和波動率,。隨著基礎(chǔ)學習器的增加，夏普比率相當,，波動率和最大回撤會緩慢增加,，收益逐步增加。 

3 結(jié)論

    使用K近鄰算法對中證500指數(shù)的漲跌進行預測,，交易上,，預測為漲時做多，預測為跌時做空?？紤]可行性,，特征數(shù)據(jù)滯后一天，還考慮交易手續(xù)費,，假設為千分之1.5,。本文得出以下結(jié)論：

    （1）單個K近鄰模型在2017年～2018年9月間取得了76.72%的累計收益（含手續(xù)費）。這一收益表現(xiàn)驗證了假設,，即股票的價格運動與過去是相似的,。

    （2）考慮K近鄰模型的內(nèi)在含義，使用不同的訓練數(shù)據(jù),，比較現(xiàn)在的股票價格運動與遙遠的歷史價格運動和剛剛過去的價格運動哪個更為相似,。預測結(jié)果表明：盡管剛剛過去的數(shù)據(jù)與現(xiàn)在的股票價格運動有更一致的宏觀背景，現(xiàn)在的股票價格運動還是與遙遠的歷史價格運動更為相似,。

    （3）使用多個KNN構(gòu)成集成學習模型,，K值是訓練數(shù)據(jù)的最優(yōu)參數(shù)17的左右鄰域。逐步增加KNN的數(shù)量t,，發(fā)現(xiàn)模型的夏普比率相當,，收益率逐漸增加，代價為波動率和最大回撤的擴大,。很難判斷最優(yōu)的數(shù)量t,，但整體而言，集成模型能夠更好地控制收益和風險間的關(guān)系,，其收益表現(xiàn)更適合作為擇時策略,。

參考文獻

[1] MALKIEL B G，F(xiàn)AMA E F.Efficient capital markets：a review of theory and empirical work[J].Journal of Finance,，1970,，25(2)：383-417.

[2] GUEGAN D.Chaos in economics and finance[J].Annual Reviews in Control，2009,，33(1)：89-93.

[3] Li Hui，Sun Jie,，Sun Boliang.Financial distress prediction based on OR-CBR in the principle of k-nearest neighbors[J].Expert Systems with Applications,，2009，36(1)：643-659.

[4] TEIXEIRA L A,，OLIVEIRA A L I.A method for automatic stock trading combining technical analysis and nearest neighbor classification[J].Expert Systems with Applications,，2010，37(1)：6885-6890.

[5] 趙俊杰.基于特征加權(quán)的KNNFP改進算法及在故障診斷中的應用[J].電子技術(shù)應用,，2011,，37(4)：113-116，121.

[6] NAYAK R K，MISHRA D,，RATH A K.A Naive SVMKNN based stock market trend reversal analysis for Indian benchmark indices[J].Applied Soft Computing,，2015，35(1)：670-680.

[7] Chen Yingjun,，Hao Yongtao.A feature weighted support vector machine and K-nearest neighbor algorithm for stock market indices prediction[J].Expert Systems with Applications,，2017，80(1)：340-355.

[8] PATEL J,，SHAH S,，THAKKAR P，et al.Predicting stock and stock price index movement using trend deterministic data preparation and machine learning techniques[J].Expert Systems with Applications,，2015,，42(1)：259-268.

[9] PATEL J，SHAH S,，THAKKAR P,，et al.Predicting stock market index using fusion of machine learning techniques[J].Expert Systems with Applications，2015,，42(1)：2162-2172.

[10] Zhang Xiaodan,，Li Ang，Pan Ran.Stock trend prediction based on a new status box method and AdaBoost probabilistic support vector machine[J].Applied Soft Computing,，2016,，49(1)：385-398.

作者信息：

張偉楠，魯統(tǒng)宇,，孫建明

(中國計量大學 經(jīng)濟與管理學院,，浙江 杭州310018)