0 引言

    當(dāng)前軍事航天飛行試驗(yàn)呈現(xiàn)出“短間隔,、快流程”的新特點(diǎn)，隨著遙測數(shù)據(jù)處理實(shí)時化,、智能的不斷發(fā)展,，遙測數(shù)據(jù)的實(shí)時判讀、快速分析顯得愈發(fā)關(guān)鍵^[1-2],。其中,，當(dāng)次飛行試驗(yàn)的遙測數(shù)據(jù)曲線變化規(guī)律與預(yù)示理論曲線變化規(guī)律是否一致、與同型號歷史數(shù)據(jù)的變化規(guī)律是否一致,，是判讀數(shù)據(jù)正確與否的重要判據(jù),，也是數(shù)據(jù)自動分析判決首要解決的問題。

    目前,，遙測數(shù)據(jù)的判決方法主要有幅值法,、包絡(luò)法和人工判讀法等，存在數(shù)據(jù)檢查依賴人工,、數(shù)據(jù)判決方法單一等不足,，效率和準(zhǔn)確率均不能滿足現(xiàn)場決策需求^[3-4]。因此,，本文提出了一種基于證據(jù)理論的遙測時序數(shù)據(jù)相關(guān)性分析的判讀方法,，將數(shù)據(jù)挖掘技術(shù)應(yīng)用到數(shù)據(jù)判讀中,，發(fā)現(xiàn)數(shù)據(jù)之間存在的關(guān)系，通過構(gòu)建Pearson相關(guān)系數(shù),、Spearman相關(guān)系數(shù),、Kendall相關(guān)系數(shù)等數(shù)據(jù)相關(guān)性分析途徑，對多次飛行試驗(yàn)的同類型遙測數(shù)據(jù)一致性進(jìn)行分析,，并通過證據(jù)理論得到評估結(jié)果,。

1 時序數(shù)據(jù)相關(guān)性分析方法

1.1 Pearson相關(guān)系數(shù)

    Pearson相關(guān)系數(shù)是一種線性相關(guān)系數(shù)，用來反映兩個變量線性相關(guān)程度的統(tǒng)計量^[5],。

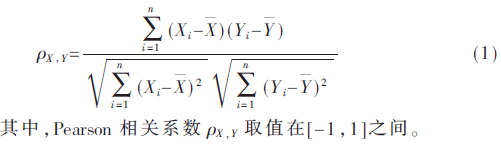
    如果將變量X變?yōu)閍+bX,，把變量Y變?yōu)閏+dY，其中a,、b,、c、d都是常數(shù),，那么,，將新的X與Y代入式(1)，可以發(fā)現(xiàn)其Pearson相關(guān)系數(shù)不會發(fā)生改變,。該系數(shù)的最典型的特性就是它并不隨著變量的位置或是大小的變化而變化,，這一點(diǎn)在工程應(yīng)用中具有良好的實(shí)用性。

    Pearson相關(guān)系數(shù)特點(diǎn)規(guī)律如下：

    (1)取1時表示Y隨著X的增大而增大,，取-1時則表示變量Y隨著X的增大而減?。?/p>

    (2)取0則是表示變量之間沒有線性相關(guān)關(guān)系,。

1.2 Spearman相關(guān)系數(shù)

    Spearman相關(guān)系數(shù)是一個非參數(shù)的(非參數(shù)性是指樣本之間精確的分布可以在不知道X和Y的聯(lián)合概率密度函數(shù)時獲得),、度量兩個變量之間的統(tǒng)計相關(guān)性的指標(biāo)，用來度量兩個變量之間聯(lián)系的強(qiáng)弱,，通常被認(rèn)為是排列后的變量之間的Pearson線性相關(guān)系數(shù)^[6],。

    Spearman相關(guān)系數(shù)特點(diǎn)規(guī)律如下：

    (1)若變量之間具有嚴(yán)格單調(diào)遞增關(guān)系，則二者的Spearman相關(guān)系數(shù)為1,，若變量之間具有嚴(yán)格單調(diào)遞減關(guān)系,，則二者的Spearman相關(guān)系數(shù)為-1；

    (2)取0則是表示變量之間沒有相關(guān)關(guān)系,。

1.3 Kendall相關(guān)系數(shù)

    Kendall相關(guān)系數(shù)又稱作和諧系數(shù),，也是一種非參數(shù)的等級相關(guān)系數(shù)^[7]。

    假設(shè)兩個變量X與Y,，它們的第i個觀察值為(x_i,，y_i)，第j個觀察值為(x_j,，y_j)(1≤i,，j≤N),。如果(x_i-x_j)(y_i-y_j)>0，則稱該數(shù)對為和諧數(shù)對,，反之為非和諧數(shù)對,。設(shè)和諧數(shù)對總數(shù)為C，非和諧數(shù)對總數(shù)為D,?？梢钥闯觯繑?shù)據(jù)的對數(shù)組合有N(N-1)/2種組合,，即C+D=N(N-1)/2,。

    于是，Kendall相關(guān)系數(shù)τ的計算公式如下：

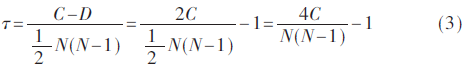
    Kendall相關(guān)系數(shù)特點(diǎn)規(guī)律如下：

    (1)若所有數(shù)對均和諧,，則τ=1,，若所有數(shù)對均非和諧，則τ=-1,；

    (2)取τ=0則是表示數(shù)據(jù)中和諧與非和諧數(shù)對勢力均衡,，沒有明顯趨勢，相關(guān)性不強(qiáng),。

2 采用證據(jù)理論實(shí)現(xiàn)多種判決結(jié)果的融合決策

    在時序數(shù)據(jù)曲線一致性判決中,，由于遙測數(shù)據(jù)在天地間傳輸過程中的信號干擾以及外部環(huán)境的影響，導(dǎo)致通過單個途徑(上述3種相關(guān)系數(shù))判斷獲取的數(shù)據(jù)與歷史數(shù)據(jù)的一致性存在不確定性和隨機(jī)性^[8],。為了提高在工程應(yīng)用中遙測數(shù)據(jù)辨識的可靠性，提高計算機(jī)自動化識別的準(zhǔn)確率,，采用證據(jù)理論方法對多種判決途徑給出的結(jié)論進(jìn)行融合判決,，實(shí)現(xiàn)多途徑判決結(jié)果的“決策級”融合識別目的^[9]。該方法能夠?qū)崿F(xiàn)各判決途徑性能和效果的互補(bǔ),，最大程度提高判決結(jié)論的正確度和可信度^[10],。

    對m_i進(jìn)行歸一化處理，即得到最終的各判決結(jié)果構(gòu)造唯一的修正基本概率分配m_i,，1≤i≤N,。

    下面即可按照證據(jù)理論的證據(jù)合成過程進(jìn)行最終結(jié)果的判決。

    對于最終的證據(jù)融合判決數(shù)值結(jié)果,，根據(jù)預(yù)設(shè)門限進(jìn)行比較,，即可得到最終的判讀決策。

3 數(shù)值實(shí)驗(yàn)

    假設(shè)Pearson關(guān)聯(lián)系數(shù)為P₁,、Spearman等級相關(guān)系數(shù)為P₂,、Kendall相關(guān)系數(shù)為P₃。對于P₁,，證據(jù)概率賦值結(jié)果為[m₁₁,，m₁₂,，m₁₃，0],；對于P₂,，證據(jù)概率賦值結(jié)果為[m₂₁，m₂₂,，m₂₃,，0]；對于P₃,，證據(jù)概率賦值結(jié)果為[m₃₁,，m₃₂，m₃₃,，0],。隨后，采用證據(jù)理論進(jìn)行融合,。融合結(jié)果為M=[m₁,，m₂，m₃,，0],，判決條件統(tǒng)一設(shè)置為：

    (1)經(jīng)驗(yàn)條件：若P₁>0.85且P₂<0.50，則判定為曲線比對結(jié)果一致,；

    (2)經(jīng)驗(yàn)條件：若P₂>0.50且P₁<0.02,，則判定為曲線比對結(jié)果一致；

    (3)若不滿足條件(1)和條件(2),，依據(jù)3個函數(shù)判斷結(jié)果進(jìn)行證據(jù)理論融合判決,，若m₁-m₂>0.60且m₃<0.05，則判定為曲線比對結(jié)果一致,；

    (4)其他結(jié)果,，則判定為曲線比對結(jié)果不一致。

    下面以某飛行器兩次飛行試驗(yàn)的模擬數(shù)據(jù)為例,，對飛行試驗(yàn)走勢方面遙測曲線的一致性自動判決結(jié)果進(jìn)行分析,，具體如圖1所示。

    Pearson相關(guān)系數(shù)為0.965 27,，Spearman等級相關(guān)系數(shù)統(tǒng)計關(guān)聯(lián)系數(shù)為0.808 53,，Kendall相關(guān)系數(shù)0.807 58，證據(jù)合成過程見表1,。通過證據(jù)理論融合判決,，認(rèn)為最終一致性判決結(jié)果m₁-m₂為0.663 65，大于預(yù)設(shè)門限值，因此決策判別該曲線變化趨勢是一致的,。

4 結(jié)論

    本文針對遙測時序數(shù)據(jù)判讀復(fù)雜問題,，提出了一種基于數(shù)據(jù)相關(guān)性分析的數(shù)據(jù)一致性自動判決方法。比較研究了3種相關(guān)系數(shù),，并通過構(gòu)建Pearson相關(guān)系數(shù),、Spearman相關(guān)系數(shù)、Kendall相關(guān)系數(shù)等途徑,，對多次飛行試驗(yàn)的同類型遙測數(shù)據(jù)一致性進(jìn)行分析,。實(shí)驗(yàn)結(jié)果表明，對多種類型的飛行試驗(yàn)數(shù)據(jù)進(jìn)行分析估計后,，評價結(jié)果在飛行穩(wěn)定時段與特征時段均能保持穩(wěn)定,，該方法對復(fù)雜多變的遙測時序數(shù)據(jù)可以快速、準(zhǔn)確,、有效地判讀,。

參考文獻(xiàn)

[1] 張東.遙測數(shù)據(jù)處理系統(tǒng)UML建模與實(shí)現(xiàn)[J].電子測量技術(shù)，2017,，40(1)：52-56.

[2] 胡泊.現(xiàn)代數(shù)字信號處理的應(yīng)用和發(fā)展前景[J].信息系統(tǒng)工程,，2017(2)：113-113.

[3] 劉鑫，任勇峰,，劉小華,，等.基于遙測數(shù)據(jù)的壓縮算法設(shè)計與實(shí)現(xiàn)[J].電子技術(shù)應(yīng)用，2008,，34(11)：79-81.

[4] 冷佳鵬,，劉文怡.一種遙測數(shù)據(jù)實(shí)時壓縮系統(tǒng)[J].電子技術(shù)應(yīng)用，2013,，39(4)：72-74.

[5] 郝德華,，關(guān)維國，鄒林杰,，等.基于Pearson相關(guān)系數(shù)的快速虛擬網(wǎng)格匹配定位算法[J].計算機(jī)應(yīng)用，2018,，38(3)：763-768.

[6] 謝文華.Spearman相關(guān)系數(shù)的變量篩選方法[D].北京：北京工業(yè)大學(xué),，2015.

[7] 于福蘭.利用Kendall模相關(guān)系數(shù)法評價地表水水質(zhì)變化趨勢[J].水利規(guī)劃與設(shè)計，2016(3)：26-27.

[8] 趙汝鵬,，田潤瀾,，王曉峰.基于證據(jù)理論的雷達(dá)信號融合識別算法改進(jìn)研究[J].電子技術(shù)應(yīng)用，2017,，43(6)：25-28.

[9] 朱菲,，金煒東.一種SVM-DS決策融合方法及在高鐵故障中的應(yīng)用[J].電子技術(shù)應(yīng)用，2018,，44(7)：127-130,，134.

[10] 于長海,，許圣濤，石玉華.多站遙測數(shù)據(jù)處理中的數(shù)據(jù)融合方法研究[J].遙測遙控,，2018(1)：47-52,，56.

[11] 吳翠翠.D-S證據(jù)理論中基于BPA的決策方法研究[D].西安：西北工業(yè)大學(xué)，2015.

作者信息:

岳  佳1,，張  磊2,，魯江偉1

(1.中國太原衛(wèi)星發(fā)射中心技術(shù)部，山西 太原030027,；2.中國電子信息產(chǎn)業(yè)集團(tuán)有限公司第六研究所,，北京100083)