文獻(xiàn)標(biāo)識(shí)碼: A
DOI:10.16157/j.issn.0258-7998.190253
中文引用格式: 張菡,薄涵亮,,王帥,,等. 電容式位移傳感器的非線性擬合比較[J].電子技術(shù)應(yīng)用,2019,,45(9):89-92,,96.
英文引用格式: Zhang Han,Bo Hanliang,,Wang Shuai,,et al. Nonlinear fitting comparison of capacitive displacement sensors[J]. Application of Electronic Technique,2019,,45(9):89-92,,96.
0 引言
控制棒是實(shí)現(xiàn)反應(yīng)堆正常啟停,、功率運(yùn)行和緊急停止的重要控制裝置[1]。當(dāng)遇到需要停堆的緊急情況時(shí),,控制棒以自由落體的方式快速落下,,達(dá)到停止反應(yīng)的安全狀態(tài)。但是控制棒在落棒期間可能遇到卡棒事故,,運(yùn)行期間可能會(huì)出現(xiàn)彈棒事故,,因此對(duì)控制棒的棒位測(cè)量至關(guān)重要。棒位測(cè)量系統(tǒng)使操作人員能夠及時(shí)發(fā)現(xiàn)控制棒是否按照指定的程序運(yùn)行和產(chǎn)生故障時(shí)的位置,,并迅速處理控制棒故障,,以確保控制棒的安全運(yùn)行,??刂瓢袈浒暨^(guò)程為直線下落運(yùn)動(dòng),當(dāng)使用電容位移傳感器測(cè)量位移時(shí),,能夠準(zhǔn)確反映電容與位移關(guān)系的方程式是知道控制棒在堆芯中位置的關(guān)鍵,。
位移測(cè)量傳感器[2-3]按照測(cè)量原理可分為電感式位移傳感器、電渦流式位移傳感器,、超聲波位移傳感器,、電容位移傳感器等[4]。其中,,電感式傳感器和電渦流式傳感器在具體實(shí)驗(yàn)中雖然具有連續(xù)測(cè)量,、精度較高等優(yōu)點(diǎn),但都會(huì)有系統(tǒng)復(fù)雜且制造困難等問(wèn)題,;超聲波傳感器具有波長(zhǎng)短,、頻率高、方向性好等優(yōu)點(diǎn),,但是易受反應(yīng)堆內(nèi)環(huán)境影響,,造成測(cè)量困難,會(huì)產(chǎn)生不小的誤差,,且超聲波傳感器由于置于控制棒外殼內(nèi)部,,使得維修不易。相比較而言,,電容傳感器具有一定的優(yōu)越性,,它具有可靠性高、響應(yīng)速度快,、測(cè)量精度高等優(yōu)點(diǎn),,且結(jié)構(gòu)簡(jiǎn)單,,使用方便。因此,,本文使用電子六所研制的電容式位移傳感器對(duì)控制棒數(shù)據(jù)進(jìn)行研究,。
控制棒落棒過(guò)程為直線下落運(yùn)動(dòng),,落棒時(shí)控制棒位移與電容值之間的關(guān)系對(duì)精確指示棒位非常重要,。本文分別使用三次樣條函數(shù)、最小二乘法和BP神經(jīng)網(wǎng)絡(luò)算法,,對(duì)位移測(cè)量得到的數(shù)據(jù)進(jìn)行曲線擬合分析,,確定位移與電容值之間的關(guān)系。
1 電容式位移傳感器測(cè)量原理
1.1 三次樣條插值擬合原理

1.2 最小二乘法擬合擬合原理

根據(jù)式(4)可知X×L=Y,,由于X和Y已知,,可根據(jù)L=(X′X)-1X′Y求得L,從而得到擬合曲線,。
1.3 BP神經(jīng)網(wǎng)絡(luò)擬合原理
BP神經(jīng)網(wǎng)絡(luò)是一種按照誤差逆?zhèn)鞑ニ惴ㄓ?xùn)練的多層前饋神經(jīng)網(wǎng)絡(luò),。通過(guò)輸入層神經(jīng)云接收外界輸入,隱層與輸入層神經(jīng)元對(duì)信號(hào)進(jìn)行加工,,然后由輸出層神經(jīng)元輸出結(jié)果,。BP神經(jīng)網(wǎng)絡(luò)模型如圖1所示。
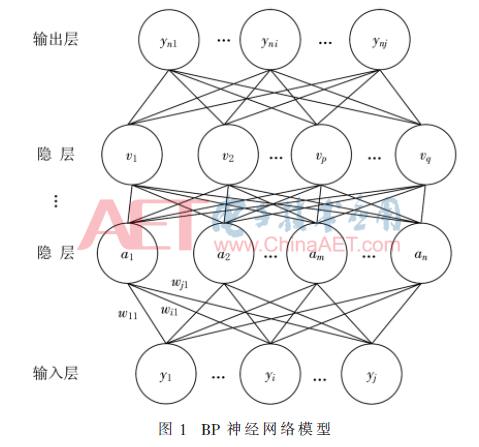
對(duì)于神經(jīng)網(wǎng)絡(luò)來(lái)說(shuō),,包含一個(gè)輸入層,、一個(gè)輸出層、n個(gè)隱層(n可以等于任意整數(shù)),。每一隱層的神經(jīng)元都可以看作下一層的輸入,,其值等于上一層與當(dāng)前神經(jīng)元相連的每一個(gè)神經(jīng)元與其權(quán)值之積的和,如:

同理可得Vn(n=1,,…,,q)的值。
BP神經(jīng)網(wǎng)絡(luò)的計(jì)算流程為將輸入實(shí)例傳送給輸入層神經(jīng)元,,然逐層將信號(hào)前傳,,直至產(chǎn)生輸出層的結(jié)果:
(1)隨機(jī)化所有的閾值和連接權(quán);
(2)計(jì)算輸出層的誤差,,將誤差反向傳播至隱層神經(jīng)元,;
(3)根據(jù)隱層神經(jīng)元的誤差來(lái)對(duì)連接權(quán)和閾值進(jìn)行調(diào)整;
(4)將步驟(2)~步驟(3)循環(huán)進(jìn)行,,直至達(dá)到終止條件[6],。
2 實(shí)驗(yàn)與分析
2.1 實(shí)驗(yàn)配置
本次實(shí)驗(yàn)采用光柵線位移傳感器為位移輸入設(shè)備,清華大學(xué)研發(fā)的電容傳感器以及與電子六所合作開(kāi)發(fā)的電容測(cè)量?jī)x及采集軟件作為電容值輸出設(shè)備,。通過(guò)控制棒位移的移動(dòng)對(duì)電容值進(jìn)行數(shù)據(jù)標(biāo)定,。
實(shí)驗(yàn)配置為:控制棒套筒尾端端子(高低電平和地線)通過(guò)線纜與測(cè)量?jī)x接口連接,,測(cè)量?jī)x通過(guò)Modbus RS-485串口與個(gè)人計(jì)算機(jī)(PC)上USB口連接,實(shí)驗(yàn)配置如圖2所示,。

經(jīng)過(guò)標(biāo)定得測(cè)得的電容值經(jīng)過(guò)測(cè)量?jī)x測(cè)量后保存在PC上,,對(duì)PC中的數(shù)據(jù)進(jìn)行擬合分析。
2.2 實(shí)驗(yàn)分析
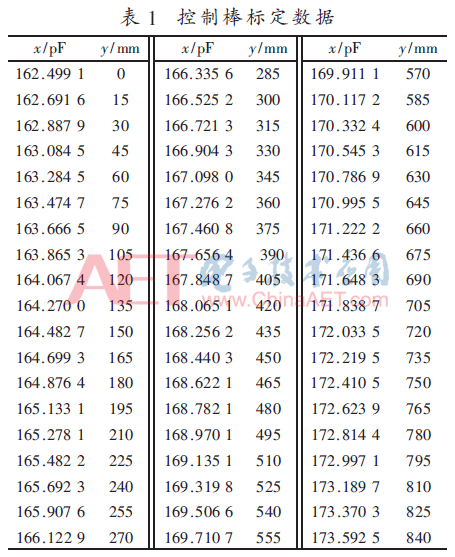
標(biāo)定實(shí)驗(yàn)的現(xiàn)場(chǎng)工況為,,數(shù)據(jù)標(biāo)定的行程為0~840 mm,,以15 mm為一步長(zhǎng)標(biāo)定電容值,一組實(shí)驗(yàn)標(biāo)定4次,,分別為:(1)控制棒水平放置時(shí),,從0 mm~840 mm逐步遞增移動(dòng);(2)控制棒水平放置時(shí),,從840 mm~0 mm逐步遞減,;(3)控制棒垂直放置時(shí),從0 mm~840 mm逐步遞增,;(4)控制棒垂直放置時(shí),,從840 mm~0 mm逐步遞減移動(dòng)。由于儀器測(cè)得的電容值存在波動(dòng),,非穩(wěn)定值,,因此以上4種情況的每個(gè)位置均測(cè)量100組電容值,取其平均值,,分別得到4組數(shù)據(jù),。
x表示在同一位移時(shí)4種情況電容值的數(shù)學(xué)期望;y為位移,,從0 mm~150 mm,,每15 mm為一步。實(shí)驗(yàn)數(shù)據(jù)如表1所示,。



通過(guò)殘差分析可以看出,,擬合精確度大約為0.04,殘差分析得到的決定系數(shù)R2為0.060 4,,統(tǒng)為計(jì)量(F值)為2.570 9,,F(xiàn)(1,n-2)分布大于F值的概率P為0.116 7,。
圖5(a),、圖5(b)分別為使用最小二乘法擬合得到的曲線圖像,圖6(a),、圖6(b)分別為實(shí)際電容值與擬合電容值之差做出的殘差圖,。其中,data1為使用最小二乘法擬合得到的曲線,,data2為驗(yàn)證點(diǎn)(x2,,y2)的值,,data3為x2通過(guò)曲線插值之后得到的擬合點(diǎn)(x2, ),,data4為用于擬合曲線的點(diǎn)(x1,,y1)。
),,data4為用于擬合曲線的點(diǎn)(x1,,y1)。

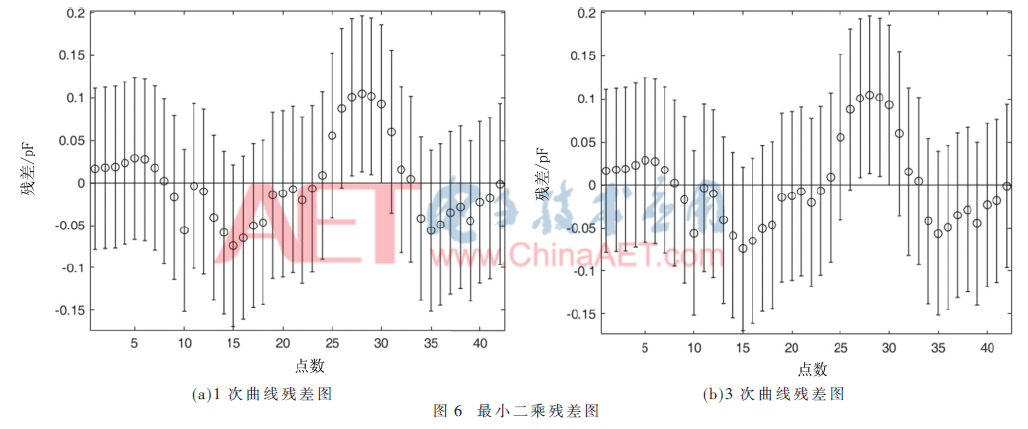
通過(guò)殘差分析可以看出,,兩種函數(shù)擬合精確度大約為0.2,、0.16,殘差分析得到的決定系數(shù)R2分別為0.009 5,、0.001 0,,統(tǒng)計(jì)量(F值)為0.383 9、0.039 4,,F(xiàn)(1,n-2)分布大于F值的概率P分別為0.539 1,、0.843 7,。
一般來(lái)說(shuō)決定系數(shù)R2越大,說(shuō)明回歸約顯著,;概率P越小,,說(shuō)明擬合模型效果越好。所以通過(guò)殘差分析可以看出與最小二乘法相比,,三次樣條的擬合效果更好,。
使用BP神經(jīng)網(wǎng)絡(luò)進(jìn)行曲線擬合,設(shè)置隱層分別為3,、9層,,參數(shù)迭代次數(shù)100次,將(x1,,y1)值作為訓(xùn)練集,,(x2,y2)作為驗(yàn)證集和測(cè)試集,,且驗(yàn)證集和測(cè)試集各占50%的比例,,分別得到的擬合函數(shù)和誤差如圖7所示。

從以上試驗(yàn)結(jié)果可以看出,,隱層次數(shù)在3層時(shí),,誤差不超過(guò)0.2;在9層時(shí),,誤差在2之間,。在控制棒標(biāo)定多次實(shí)驗(yàn)中,BP神經(jīng)網(wǎng)絡(luò)算法擬合曲線時(shí)隱層在3~6時(shí),,擬合效果相對(duì)更好,。雖然利用BP神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)和泛化能力可以很好地?cái)M合出控制棒棒位移動(dòng)時(shí)位移與電容值之間的特性曲線,,但是無(wú)法得到確定的某一擬合方程式,在測(cè)量?jī)x中實(shí)現(xiàn)較為困難,,以至于在現(xiàn)場(chǎng)中無(wú)法使用,,相比較而言,三次樣條函數(shù)和最小二乘法更易得到擬合曲線,。
在殘差分析圖中,,三次樣條函數(shù)和最小二乘法均存在異常點(diǎn),經(jīng)過(guò)分析懷疑是重力原因,,由于控制棒在套筒內(nèi)由于重力原因無(wú)法正好在套筒的正中心,,可能導(dǎo)致控制棒在移動(dòng)時(shí)稍微向下傾斜,導(dǎo)致存在異常點(diǎn),,暫時(shí)無(wú)法避免,,并且沒(méi)有好的方法進(jìn)行驗(yàn)證。
3 結(jié)論
本文使用MATLAB,,通過(guò)三次樣條插值,、最小二乘法和BP神經(jīng)網(wǎng)絡(luò)三種方法,對(duì)控制棒位移測(cè)量數(shù)據(jù)進(jìn)行了擬合分析,。由于與最小二乘法相比,,三次樣條插值的擬合效果;與BP神經(jīng)網(wǎng)絡(luò)相比,,三次樣條插值更易得到擬合公式,,易于插值。綜合而言,,在反應(yīng)堆控制棒落棒時(shí),,使用三次樣條插值得到的函數(shù)效果更好。
參考文獻(xiàn)
[1] 張濤.基于數(shù)字圖象處理技術(shù)的光學(xué)位移測(cè)量方法的研究[D].哈爾濱:中國(guó)地震局工程力學(xué)研究所,,2011.
[2] 吳軼,,李青,施閣.一種用于地下位移測(cè)量傳感器串的無(wú)線電能傳輸裝置設(shè)計(jì)[J].電子技術(shù)應(yīng)用,,2018,,44(7):155-159.
[3] 焦萬(wàn)果,李昱融,,周雯.能量收集認(rèn)知傳感器網(wǎng)絡(luò)綜述研究[J].電子技術(shù)應(yīng)用,,2015,44(10):23-28.
[4] 王曉立.電容式位移傳感器研究[D].湘潭:湘潭大學(xué),,2010.
[5] SAUER T.數(shù)值分析[M].裴玉茹,,馬賡宇,譯.北京:機(jī)械工業(yè)出版社,2014.
[6] 周志華.機(jī)器學(xué)習(xí)[M].北京:清華大學(xué)出版社,,2016.
作者信息:
張 菡1,,薄涵亮2,王 帥1,,楊文龍1,,傅一帆1
(1.華北計(jì)算機(jī)系統(tǒng)工程研究所,北京100083,;2.清華大學(xué) 核能與新能源技術(shù)研究院,,北京100084)

