0 引言

    圖像分割是圖像處理中的一個(gè)關(guān)鍵步驟，也是圖像分析和理解的基礎(chǔ),，對(duì)圖像目標(biāo)進(jìn)行提取,、測(cè)量都離不開(kāi)圖像分割^[1]。

    目前,，國(guó)內(nèi)外學(xué)者采用不同方法對(duì)圖像分割問(wèn)題做了大量研究^[2-3],，這些方法各有優(yōu)勢(shì)，也存在一些問(wèn)題,。例如,，基于圖論的圖像分割是一個(gè)研究熱點(diǎn)，但此法屬于NP-hard問(wèn)題,，也就是隨著圖中節(jié)點(diǎn)數(shù)的增大，問(wèn)題的求解將變得復(fù)雜耗時(shí),。另外,，目前還沒(méi)有能夠精確求出最優(yōu)解的算法，實(shí)際中一般采用近似的求解算法,，這使得圖像分割中不可避免地存在一些誤差,，從而影響圖像處理的效果。而遺傳算法能使這些誤差最小,，從而使計(jì)算機(jī)視覺(jué)達(dá)到實(shí)用化的要求,。而且，遺傳算法進(jìn)行圖像處理時(shí)不像傳統(tǒng)算法那樣局限于鄰域特性的最佳,，而是考慮整幅圖像的最佳,，使圖像處理效果接近人眼的觀察效果^[4-6]。

1 使用遺傳算法進(jìn)行圖像分割的思路

    圖像分割關(guān)鍵因素是獲得灰度圖片的分割閾值,。因此,，在用遺傳算法處理時(shí)，首先要用染色體表示閾值,，目標(biāo)是選出最佳閾值染色體,。同時(shí)，應(yīng)確立最佳閾值的評(píng)價(jià)指標(biāo),，也就是適應(yīng)度函數(shù)的建立,。

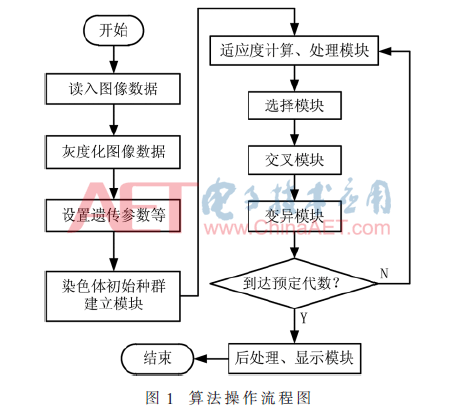
    圍繞這個(gè)主題，首先要建立染色體初始種群,；而后,，調(diào)用適應(yīng)度計(jì)算模塊，計(jì)算種群中各個(gè)染色體的適應(yīng)度值，接著按照適應(yīng)度值對(duì)種群中的染色體進(jìn)行排序,，并記錄該代種群的最佳閾值,；在選擇步驟中，按照一定規(guī)則用上一代適應(yīng)度大的個(gè)體替代當(dāng)前代適應(yīng)度小的個(gè)體組成新的種群,；進(jìn)入交叉處理環(huán)節(jié)后,，按照設(shè)定的比例采用某種方式（例如隨機(jī)方式）選擇需要進(jìn)行交叉的染色體對(duì)，在此過(guò)程中將產(chǎn)生不同于前輩的新的染色體個(gè)體,；執(zhí)行變異步驟,，在此步，將按照設(shè)定的概率,，以一定的方式（例如隨機(jī)）找出發(fā)生變異的染色體基因位置,，這個(gè)過(guò)程同樣會(huì)產(chǎn)生全新的個(gè)體；當(dāng)變異步驟執(zhí)行完后,，再次回到適應(yīng)度計(jì)算步驟循環(huán)進(jìn)行,，直到達(dá)到設(shè)定的遺傳代數(shù)^[7-8]；最后,，依據(jù)算法給出的最佳閾值對(duì)圖片進(jìn)行處理并顯示,。算法的流程如圖1所示。

2 算法中主要模塊的設(shè)計(jì)

2.1 預(yù)處理和初始種群生成模塊

    在預(yù)處理步驟中需要設(shè)計(jì)染色體表示方法,。由于本文中灰度圖的閾值最高限為255,，是一個(gè)數(shù)值，因此這里采用二進(jìn)制表示法即可^[9],。二進(jìn)制的位數(shù)由式(1)確定,。

其中，b_j,、a_j分別表示染色體描述變量區(qū)間的最大和最小值,，m_j表示采用的二進(jìn)制位數(shù)。本文中閾值的取值范圍為[0,，255],，代入式(1)可以求得m_j=8，也即本文中用8位二進(jìn)制表示染色體個(gè)體,。為考慮整幅圖像最佳,，這里判別染色體個(gè)體優(yōu)劣的適應(yīng)度函數(shù)采用式(2)來(lái)描述。

其中,，p₁,、p₂分別表示目標(biāo)像素和背景像素的個(gè)數(shù)，μ₁,、μ₂分別表示目標(biāo)像素和背景像素的平均灰度值,，f表示適應(yīng)度值,。

    在算法的初始化操作中，采用隨機(jī)生成的方案隨機(jī)生成10個(gè)8位的染色體,，構(gòu)成初始種群,。交叉概率和變異概率分別設(shè)置為0.7和0.2。

2.2 適應(yīng)度計(jì)算模塊

    在此操作過(guò)程中要設(shè)置代溝,，這里設(shè)置為0.9,，也就是將要淘汰10%的較差個(gè)體^[10]。在第二代以后的群體中,，將90%的更優(yōu)秀的個(gè)體保留進(jìn)入后續(xù)處理程序,；對(duì)群體中保留下來(lái)的個(gè)體計(jì)算其對(duì)應(yīng)的閾值；分別統(tǒng)計(jì)低于和高于閾值的灰度值的總個(gè)數(shù)和總和,，繼而求出兩類(lèi)灰度的平均值,，根據(jù)式(2)計(jì)算出對(duì)應(yīng)于每條染色體的適應(yīng)度值；對(duì)于本代和上一代,，根據(jù)適應(yīng)度值由小到大對(duì)染色體進(jìn)行排序,；統(tǒng)計(jì)每一代的最佳閾值和最佳適應(yīng)度值。閾值到灰度值的轉(zhuǎn)化見(jiàn)式(3),。

式中,，h是灰度值，c是染色體對(duì)應(yīng)的十進(jìn)制數(shù)值,，l是二進(jìn)制染色體長(zhǎng)度。

    本步驟的算法流程如圖2所示,。

2.3 選擇模塊,、交叉模塊和變異模塊

    在選擇步驟中，首先計(jì)算前一代中適應(yīng)度值比當(dāng)前群體適應(yīng)度值大的個(gè)體及其數(shù)量,；而后,，用上一代適應(yīng)度比當(dāng)前代更大的個(gè)體隨機(jī)取代當(dāng)前代的個(gè)體；最后,，將當(dāng)前代的各項(xiàng)數(shù)據(jù)保存,。

    在交叉操作中，首先依據(jù)交叉概率隨機(jī)地選出參與交叉的染色體對(duì),；然后,，按照隨機(jī)選擇方案選出交叉點(diǎn)位置進(jìn)行交叉，這里的交叉選用單點(diǎn)交叉即可^[11],。

    在變異操作中^[12],，首先依據(jù)設(shè)置的變異概率計(jì)算出在群體中所有的基因里參與變異的基因數(shù)量；使用隨機(jī)選取的方式確定變異基因所在的行列位置,，然后對(duì)選擇的變異基因進(jìn)行取反操作,；保存處理過(guò)的種群,；最后，用上一代中最優(yōu)的染色體補(bǔ)充到當(dāng)前代群體中,，以維持種群中染色體的數(shù)量,。

    上述幾部分操作的流程圖如圖3所示。

3 使用傳統(tǒng)遺傳算法進(jìn)行圖像分割的實(shí)例

    為驗(yàn)證上述傳統(tǒng)遺傳算法的效果,，應(yīng)用該法對(duì)某帶有底部噪聲的電力電子逆變系統(tǒng)圖片進(jìn)行了處理,。

    原始圖像如圖4所示，處理后的圖像如圖5所示,，最佳適應(yīng)度值進(jìn)化曲線如圖6所示,。

    由處理結(jié)果可見(jiàn)，傳統(tǒng)遺傳算法在進(jìn)化過(guò)程執(zhí)行到20代左右就已經(jīng)收斂到最佳值了,，而且能將底部顏色和文字噪聲徹底清除,，比較清晰地分割出目標(biāo)圖像。但是,，傳統(tǒng)算法處理的時(shí)間過(guò)長(zhǎng),，系統(tǒng)顯示運(yùn)算時(shí)間為7.416 s，這么長(zhǎng)的處理時(shí)間是無(wú)法滿足需求的,。

4 遺傳算法的改進(jìn)及算法改進(jìn)前后圖像實(shí)際處理效果的比較

4.1 算法的改進(jìn)

    遺傳算法若要收斂到全局最優(yōu)解必須具備拓展性和收斂性,，而這些性能與交叉概率p_c和變異概率p_m密切相關(guān)^[13-14]。增大p_c的值,，雖然加強(qiáng)了對(duì)新的解空間拓展能力,，但增大了高適應(yīng)度的染色體結(jié)構(gòu)被破壞的可能性；反之則會(huì)減緩算法的搜索進(jìn)程,，甚至停滯,。如果p_m的值設(shè)定得過(guò)小，則可能造成早熟收斂,；反之,，則會(huì)使算法變成一個(gè)純粹的隨機(jī)過(guò)程。傳統(tǒng)遺傳算法的p_c和p_m值在算法的運(yùn)行過(guò)程中是固定不變的,。同時(shí),，從上面的算例可以看出，傳統(tǒng)的遺傳算法在圖像分割中用時(shí)較長(zhǎng),，難以滿足現(xiàn)代社會(huì)對(duì)高效運(yùn)行的需求,。因此，為了提高運(yùn)算效果和效率,，需要對(duì)算法做出改進(jìn),。

    為了克服存在的問(wèn)題，在前人工作的基礎(chǔ)上,，運(yùn)用一種自適應(yīng)方法對(duì)傳統(tǒng)算法進(jìn)行了改進(jìn)^[15],。它根據(jù)進(jìn)化的代數(shù)自適應(yīng)地調(diào)整種群的p_c和p_m,。在進(jìn)化初期取較大p_c的值，利用其全局搜索能力加強(qiáng)對(duì)新的解空間的拓展,，從而使種群進(jìn)行全局進(jìn)化,；隨著進(jìn)化的進(jìn)行，高性能的解開(kāi)始增多,，這時(shí)應(yīng)逐步減少pc值以減少對(duì)這些解的破壞,，同時(shí)，應(yīng)逐步提高p_m的值來(lái)維持種群的多樣性,，避免收斂到局部最優(yōu)解,；在進(jìn)化后期，搜索已經(jīng)接近最優(yōu)解鄰域,，這時(shí)應(yīng)主要利用p_m的局部搜索能力,，使種群在局部重點(diǎn)進(jìn)化，加速算法向最優(yōu)解收斂,。

    同時(shí),，p_c和p_m還應(yīng)與個(gè)體的適應(yīng)度值相關(guān)。對(duì)于同一代中的所有個(gè)體,，適應(yīng)度高的和低的個(gè)體發(fā)生交叉和變異的可能性應(yīng)有差異,。這能避免一些問(wèn)題，例如,，高性能的解不會(huì)和其他解一樣受到同樣的破壞,，低性能的解不會(huì)和其他解一樣被保留，這樣就就確保了遺傳算法能如預(yù)期一樣在交叉的作用下接近最優(yōu)解鄰域,，再在變異的作用下收斂到最優(yōu)解,。為此，應(yīng)根據(jù)遺傳代數(shù)和適應(yīng)度值共同自適應(yīng)地調(diào)整p_c,、p_m。對(duì)于適應(yīng)度高于種群平均水平的個(gè)體,，應(yīng)設(shè)定較小的p_c和p_m,，使它們?cè)谶M(jìn)化中能得到較好的保護(hù)；反之亦然,，使低適應(yīng)度個(gè)體在進(jìn)化中更可能被淘汰,。

    在用傳統(tǒng)算法進(jìn)行圖片處理時(shí)發(fā)現(xiàn)p_c和p_m的設(shè)置大小對(duì)運(yùn)行速度影響較大，尤其是p_m,。因此,，若開(kāi)始p_m較小，會(huì)加快算法的運(yùn)算速度,。結(jié)合上述分析,，這里給出改進(jìn)后的自適應(yīng)遺傳算子(p_c和p_m)的計(jì)算公式如式(4),、式(5)所示。

    另外,，為了使進(jìn)化過(guò)程更好地體現(xiàn)優(yōu)勝劣汰,，并加快算法的收斂速度，在選擇模塊,，根據(jù)進(jìn)化代數(shù)分段選擇了替換染色體的方法,。具體為，在前三分之一代,，采用最優(yōu)個(gè)體隨機(jī)替換前代個(gè)體的方法,；在中間進(jìn)化段，采用前代最優(yōu)個(gè)體替換當(dāng)代最差個(gè)體的方法,；在后三分之一代,，使用上一代一半最優(yōu)個(gè)體替代當(dāng)前代中最差的一半的方法，加速算法尋優(yōu)過(guò)程,。

4.2 圖像處理實(shí)例及算法改進(jìn)前后處理效果的比較

    為驗(yàn)證改進(jìn)后的遺傳算法的效果,，仍然使用圖4所示原始照片，并應(yīng)用改進(jìn)后的算法對(duì)圖片進(jìn)行處理,。處理后的圖像和圖5相似,，目標(biāo)圖像被完全剔除了噪聲，變得非常清晰,。改進(jìn)算法的最佳適應(yīng)度值進(jìn)化曲線如圖7所示,。

    由處理結(jié)果可知，改進(jìn)后的遺傳算法在進(jìn)化過(guò)程執(zhí)行到8代左右就已經(jīng)收斂到最佳值了,，收斂更快,。相比較前面的分割效果而言，處理的時(shí)間較短,，僅為0.751 s,，運(yùn)算效率提高了近10倍，改進(jìn)效果顯著,。

5 結(jié)束語(yǔ)

    本文結(jié)合圖像分割詳細(xì)闡述了傳統(tǒng)遺傳算法的設(shè)計(jì)思想及其主要構(gòu)成模塊的工作機(jī)制,。在此基礎(chǔ)上，結(jié)合前人的工作給出了遺傳算法的改進(jìn)算法,。傳統(tǒng)遺傳算法對(duì)噪聲圖片的分割處理表明遺傳算法可以將目標(biāo)圖像從存在噪聲和底色的背景中分離出來(lái),，而改進(jìn)的遺傳算法則擁有更好的效果和更高的效率。這說(shuō)明遺傳算法可以成功應(yīng)用于圖像處理技術(shù)中,，改進(jìn)的遺傳算法可以有效地應(yīng)用于更為深入的圖像處理研究中,。

參考文獻(xiàn)

[1] 周莉莉，姜楓.圖像分割方法綜述研究[J].計(jì)算機(jī)應(yīng)用研究,2017,，34(7)：1921-1928.

[2] 唐思源,，楊敏,，苗玥，等.區(qū)域生長(zhǎng)和水平集相融合的肺部CT圖像分割[J].電子技術(shù)應(yīng)用,，2018,，44(5)：135-139.

[3] 張瑞華.基于ECCC的細(xì)胞圖像分割算法[J].電子技術(shù)應(yīng)用，2016,，42(7)：126-129.

[4] LI Q,，URAL S，ANDERSON J,，et al.A fuzzy Mean-Shift approach to lidar waveform decomposition[J].IEEE Transactions on Geoscience & Remote Sensing,，2016，54(12)：7112-7121.

[5] DU Z,，ZHANG G,，WANG C.Research on algorithm of small target detection and preprocessing in infrared image[J].Computer & Digital Engineering，2003(4)：31-34.

[6] HU X.Image segmentation based on graph theory in multicolor space for maize leaf disease[J].Transactions of the Chinese Society for Agricultural Machinery,，2013,，44(2)：177-181.

[7] YANG J A，TAO L,，ZHUANG Z,，et al.Research and realization of image separation method based on independent component analysis and genetic algorithm[J].Proceedings of SPIE，2002,，4875(2)：575-582.

[8] GOLDBERG D E.Genetic algorithms in search, optimization and machine learning[M].Addison-Wesley Professional,，1989.

[9] TIAN F，YAO A M,，SUN X P,，et al.Dual population genetic algorithm based on individual similarity[J].Computer Engineering and Design，2011,，32(5)：1989-1993.

[10] ANDERSON-COOK C M.Practical genetic algorithms[J].Publications of the American Statistical Association,，2004，100(471)：1099-1099.

[11] ZENG X Y,，CHEN Y W,，NAKAO Z，et al.Signal separation by independent component analysis based on a genetic algorithm[C].International Conference on Signal Processing.IEEE,，2000.

[12] SRINIVAS M，PATNAIK L M.Adaptive probabilities of crossover and mutation in genetic algorithms[J].IEEE Transactions on Systems Man & Cybernetics,，2002,，24(4)：656-667.

[13] 游培寒，畢篤彥,，馬時(shí)平.自適應(yīng)權(quán)值調(diào)整GS圖像分割算法[J].中國(guó)圖象圖形學(xué)報(bào),，2018,，11(7)：959-964.

[14] WANG B，YAN P,，ZHOU Q,，et al.State recognition method for machining process of a large spot welder based on improved genetic algorithm and hidden Markov model[J].Proceedings of the Institution of Mechanical Engineers，2017,，231(11)：2135-2146.

[15] CANTU-PAZ E.On random numbers and the performance of genetic algorithms[J].Computer Science Preprint Archive,，2002(10)：203-210.

作者信息:

安  霆

(臨沂大學(xué) 自動(dòng)化與電氣工程學(xué)院，山東 臨沂276000)