0 引言

    當(dāng)今社會(huì)信息化飛速發(fā)展，物理不可克隆函數(shù)(Physical Unclonable Function,，PUF)的不斷完善為保證信息安全提供了全新的方法^[1-2],。基于FPGA架構(gòu)的Glitch PUF首先由ANDERSON J H等^[3]提出,，文獻(xiàn)[4]在其基礎(chǔ)上,，使用多路選擇器鏈，增加了一個(gè)新的激勵(lì)比特位,，增強(qiáng)了隨機(jī)性和可擴(kuò)展性,。文獻(xiàn)[5]、[6]充分利用FPGA資源,，根據(jù)不同工藝的FPGA和不同類別的Slice分別設(shè)計(jì)了相應(yīng)的布局布線,，使得電路資源利用率顯著提升。文獻(xiàn)[5]還改進(jìn)了單元電路結(jié)構(gòu),，提升了輸出響應(yīng)0/1的平衡性。

    以上文獻(xiàn)從提升Glitch PUF隨機(jī)性的角度出發(fā),，提出了不同的改進(jìn)方案,，但都未涉及Glitch PUF輸入輸出映射關(guān)系的分析，因此不能從根本解決Glitch PUF的安全性問(wèn)題,。文獻(xiàn)[7]提出使用2-DL表示RO PUF,，并用PAC學(xué)習(xí)框架對(duì)RO PUF進(jìn)行學(xué)習(xí)，證明RO PUF可以被機(jī)器學(xué)習(xí)攻擊,。文獻(xiàn)[8]提出可用邏輯回歸(Logistic Regression)和演化策略(Evolution Strategies)方法攻擊PUF,，并對(duì)Arbiter PUF,、XOR Arbiter PUF、Feed-Forward Arbiter PUF,、Lightweight Secure PUF和RO PUF分別進(jìn)行了機(jī)器學(xué)習(xí)攻擊,。實(shí)驗(yàn)表明當(dāng)收集到一定數(shù)量的激勵(lì)響應(yīng)對(duì)(Challenge Response Pairs，CRPs)時(shí),，這些電路均可被成功預(yù)測(cè),，預(yù)測(cè)精度可達(dá)99.9%。

    本文對(duì)Glitch PUF進(jìn)行了深入研究,，針對(duì)其輸入輸出的映射關(guān)系,，提出使用MLP算法對(duì)其進(jìn)行機(jī)器學(xué)習(xí)攻擊，并通過(guò)實(shí)驗(yàn)評(píng)估方案的可行性,。

1 Glitch PUF

1.1 Glitch PUF架構(gòu)

    Glitch PUF本質(zhì)是利用FPGA上的路徑延遲差產(chǎn)生競(jìng)爭(zhēng)冒險(xiǎn)現(xiàn)象,，以此來(lái)產(chǎn)生毛刺，決定PUF單元電路的輸出為邏輯“0”或者“1”,。由于在制造的過(guò)程中,，電路的延時(shí)差異是由于工藝制作差異隨機(jī)產(chǎn)生的，即使是相同的電路結(jié)構(gòu)也很難復(fù)制出相同的延時(shí),，因此利用此原理的電路具有唯一性和物理不可克隆性,。

    Glitch PUF單元電路由兩個(gè)移位寄存器、兩個(gè)雙路數(shù)據(jù)選擇器和一個(gè)異步置位D觸發(fā)器組成,，如圖1所示,。移位寄存器的輸入邏輯相反，分別為Ox5555(0101…0101)和OxAAAA(1010…1010),，連接到數(shù)據(jù)選擇器的控制端,。兩個(gè)數(shù)據(jù)選擇器形成傳輸路徑，在理想情況下,，頂層數(shù)據(jù)選擇器的輸出為邏輯0,。異步置位D觸發(fā)器的輸入初始值為邏輯0，因此單元電路輸出為邏輯0,。但在實(shí)際電路中,，寄存器轉(zhuǎn)換延時(shí)和路徑傳輸延時(shí)不同，導(dǎo)致路徑延時(shí)差不同,，從而頂層數(shù)選器的輸出會(huì)產(chǎn)生毛刺,。毛刺傳遞到異步D觸發(fā)器的異步置位端，控制電路產(chǎn)生邏輯0/1,。由于毛刺在傳遞過(guò)程中可能會(huì)受到傳輸路徑的影響,，寬度較窄的毛刺會(huì)被過(guò)濾掉。只有寬度足夠大的毛刺,，才能使得單元電路產(chǎn)生邏輯1,。

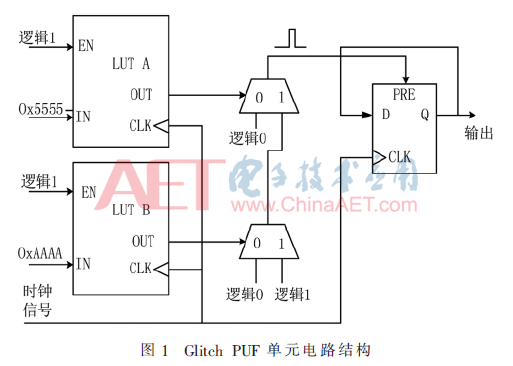
    Glitch PUF單元電路沒(méi)有外界輸入,，輸出結(jié)果完全依賴于電路制作過(guò)程中的隨機(jī)變量，因此具有很高的抗建模攻擊能力,。Glitch PUF單元電路中異步置位D觸發(fā)器的輸入端與輸出端相連,，使得單元電路穩(wěn)定地輸出邏輯0/1，這在一定程度上提高了電路的穩(wěn)定性,，但從攻擊角度來(lái)看,，這樣的設(shè)計(jì)使得電路更容易受到攻擊。為使得Glitch PUF可用于身份識(shí)別與認(rèn)證等領(lǐng)域,，ANDERSON J H設(shè)計(jì)了與RO PUF相似的Glitch PUF架構(gòu),，如圖2所示，虛線框內(nèi)為n個(gè)單元電路,，通過(guò)輸入激勵(lì)C選取不同的單元電路,，異或后輸出Glitch PUF的響應(yīng)。

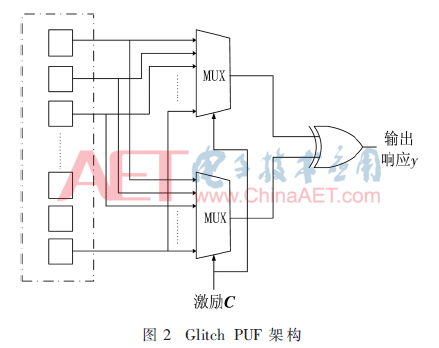
1.2 Glitch PUF模型分析

    Glitch PUF單元電路的輸出值是由傳輸延時(shí)和轉(zhuǎn)換延時(shí)決定的,，根據(jù)統(tǒng)計(jì)靜態(tài)時(shí)序分析(Statistical Static Timing Analysis,，SSTA)^[9]，延時(shí)Δ的分布符合平均值為μ,、方差為σ的高斯分布N(μ,，σ²)，且Δ落在區(qū)間[μ-3σ,，μ+3σ]的概率為99.7%,。

2 基于MLP算法的機(jī)器學(xué)習(xí)攻擊

2.1 數(shù)據(jù)處理

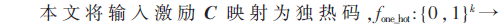
2.2 MLP算法

    機(jī)器學(xué)習(xí)能夠?qū)UF電路實(shí)現(xiàn)攻擊的主要原因是PUF電路的結(jié)構(gòu)相對(duì)固定，產(chǎn)生的大量激勵(lì)響應(yīng)對(duì)具有一定的線性特性,，使得機(jī)器學(xué)習(xí)能夠預(yù)測(cè)延遲信息和生成信息之間的關(guān)系,，從而實(shí)現(xiàn)對(duì)電路的攻擊。機(jī)器學(xué)習(xí)算法中,，線性可分?jǐn)?shù)據(jù)對(duì)于大部分算法來(lái)講是容易處理的,，但對(duì)于非線性可分?jǐn)?shù)據(jù)卻不能進(jìn)行有效的學(xué)習(xí)預(yù)測(cè)。Glitch PUF電路正是利用這一點(diǎn),，使用異或輸出,，增加電路輸出的非線性，以此增加抗建模攻擊性能,。

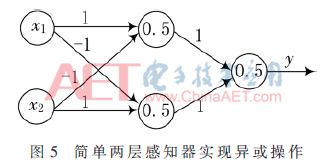
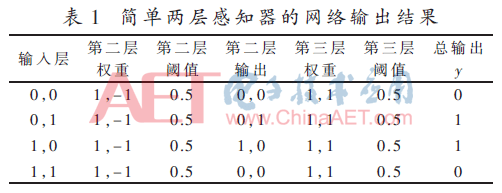
    圖4單層感知器由兩層神經(jīng)元組成,，可以輕松實(shí)現(xiàn)邏輯與、或,、非等運(yùn)算，但是由于只有一層功能神經(jīng)元,，對(duì)于簡(jiǎn)單的非線性可分問(wèn)題(如異或運(yùn)算)就不能夠正確實(shí)現(xiàn)^[10],。為解決這一問(wèn)題,，多層感知器(Multilayer Perceptron，MLP)應(yīng)運(yùn)而生,。根據(jù)普適逼近原理,，多層感知器通過(guò)增加隱藏層(Hidden Layer)和激活函數(shù)可以逼近任意函數(shù)，將非線性問(wèn)題表示為更高維度的線性問(wèn)題^[11],。采用的激活函數(shù)為閾值函數(shù),，即輸入大于閾值時(shí)可被激活，輸出為“1”,，反之則未被激活,，輸出為“0”。解決異或問(wèn)題,，使用如圖5所示的簡(jiǎn)單兩層感知器就可以實(shí)現(xiàn),。圖5中第一層為輸入層，第二層為隱藏層,，第三層為輸出層,，第二層第三層圓圈內(nèi)數(shù)字為閾值，橫線上數(shù)字為權(quán)重,，y為輸出,。網(wǎng)絡(luò)輸出結(jié)果如表1所示。兩層感知器實(shí)現(xiàn)了輸入數(shù)據(jù)的異或操作,。

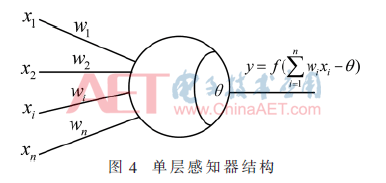
    具體來(lái)說(shuō),，多層感知器就是在單層感知器的基礎(chǔ)上增加了隱藏層，即單層的輸入輸出模型為y=f(x,，w,，θ)，而多層感知器輸入層到隱藏層模型為h=f₁(x,，w_i,，θ_i)，隱藏層的輸出作為下一層的輸入,，即y=f₂(h,，w_j，θ_j),，所以多層感知器的最終輸入輸出模型為y=f_n(f_i(f₂(f₁(x,，w，θ)))),。

    當(dāng)多層感知器輸出與樣本一致時(shí),，則權(quán)重和閾值不改變；當(dāng)多層感知器輸出與樣本輸出不一致時(shí),，權(quán)重和閾值會(huì)進(jìn)行改變,。以此方式迭代進(jìn)行,，直至符合條件。最后保存權(quán)重和閾值進(jìn)行模型建立,，然后對(duì)分類錯(cuò)誤的樣本數(shù)量進(jìn)行統(tǒng)計(jì),，輸出錯(cuò)誤率。

    多層感知器算法對(duì)Glitch PUF攻擊的具體算法偽代碼描述如下,。

3 實(shí)驗(yàn)評(píng)估

    本文采用Python建立Glitch PUF模型,，模擬其輸入與輸出的映射關(guān)系，并收集其激勵(lì)響應(yīng)對(duì),，用于后續(xù)的機(jī)器學(xué)習(xí)攻擊,。機(jī)器學(xué)習(xí)使用數(shù)據(jù)挖掘軟件WEKA，對(duì)單元數(shù)量為32,、64,、128、256的Glitch PUF進(jìn)行建模攻擊,，采用MLP算法,，十折交叉驗(yàn)證得到的攻擊錯(cuò)誤率及所需激勵(lì)響應(yīng)對(duì)數(shù)量如圖6所示。

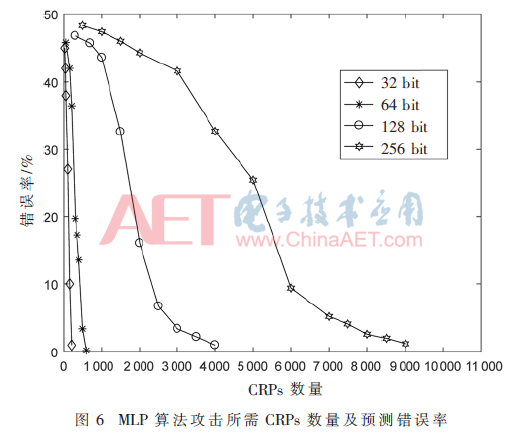
    由圖6可以看出,，PUF單元數(shù)目越多,，則攻擊所需的激勵(lì)響應(yīng)對(duì)就越多，提高預(yù)測(cè)精度也越困難,。單元電路數(shù)量越少,，增加輸入到WEKA中的激勵(lì)響應(yīng)對(duì)數(shù)量，錯(cuò)誤率幾乎呈直線下降,。圖中128 bit與256 bit的折線顯示,，當(dāng)輸入的激勵(lì)響應(yīng)對(duì)達(dá)到一定數(shù)量時(shí)，錯(cuò)誤率降低速率放緩,，基本保持不變,，這表明機(jī)器學(xué)習(xí)模型已接近最優(yōu)值，迭代可以結(jié)束,。

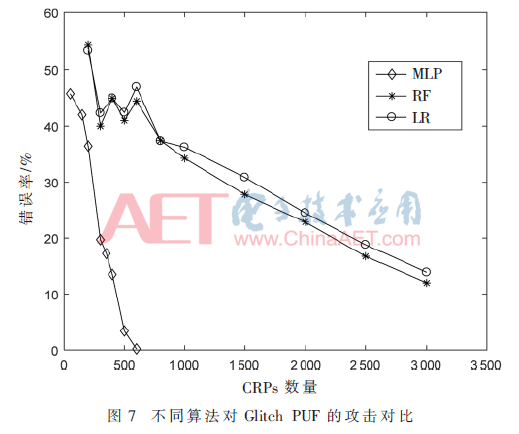
    為驗(yàn)證MLP算法對(duì)Glitch PUF攻擊的優(yōu)越性,，本文參考文獻(xiàn)[8]、[12],、[13]采用針對(duì)二分類數(shù)據(jù)常用的算法——隨機(jī)森林(RF)和邏輯回歸(LR)算法進(jìn)行對(duì)比,。以64 bit的Glitch PUF激勵(lì)響應(yīng)對(duì)數(shù)據(jù)作為樣本，測(cè)試結(jié)果如圖7所示,。從圖可以看出,，隨機(jī)森林和邏輯回歸算法在對(duì)Glitch PUF攻擊能力上基本保持一致，邏輯回歸算法的攻擊效果略低于隨機(jī)森林，多層感知器算法攻擊能力最強(qiáng),。MLP算法的預(yù)測(cè)錯(cuò)誤率在樣本數(shù)量為600左右時(shí),，已低于1%。隨機(jī)森林和邏輯回歸算法在樣本數(shù)量小于1 000時(shí),，其預(yù)測(cè)錯(cuò)誤率出現(xiàn)波動(dòng)，說(shuō)明算法不能很好地針對(duì)數(shù)據(jù)建立模型,；而后不斷增大樣本數(shù)量,，其預(yù)測(cè)錯(cuò)誤率出現(xiàn)下降趨勢(shì)。但當(dāng)樣本數(shù)量達(dá)到2 500時(shí),，其錯(cuò)誤率仍保持在20%左右,。可見(jiàn)針對(duì)Glitch PUF的機(jī)器學(xué)習(xí)攻擊,，本文所提的MLP算法的處理能力遠(yuǎn)強(qiáng)于其他兩種算法,。

4 結(jié)論

    PUF的不斷完善使其能夠應(yīng)用于信息安全領(lǐng)域，但隨著攻擊技術(shù)的不斷進(jìn)步,，其安全性也面臨著越來(lái)越多的挑戰(zhàn),。本文分析了基于FPGA的Glitch PUF的物理架構(gòu)，針對(duì)其單元電路輸出的缺陷,，分析其輸入輸出映射關(guān)系,，使用獨(dú)熱碼處理其激勵(lì)響應(yīng)對(duì)，采用MLP算法對(duì)其進(jìn)行機(jī)器學(xué)習(xí)攻擊,，成功攻擊并預(yù)測(cè)了Glitch PUF的輸出,。

參考文獻(xiàn)

[1] 張紫楠，郭淵博.物理不可克隆函數(shù)綜述[J].計(jì)算機(jī)應(yīng)用,，2012,，32(11)：3115-3120.

[2] 尹魏昕，賈詠哲,，高艷松,，等.物理不可克隆函數(shù)(PUF)研究綜述[J].網(wǎng)絡(luò)安全技術(shù)與應(yīng)用，2018(6)：41-42,，54.

[3] ANDERSON J H. A PUF design for secure FPGA-based embedded systems[C].Design Automation Conference.IEEE,，2010.

[4] Huang Miaoqing，Li Shiming.A delay-based PUF design using multiplexers on FPGA[C].IEEE International Symposium on Field-programmable Custom Computing Machines.IEEE Computer Society,，2013.

[5] 龐子涵.FPGA的物理不可克隆函數(shù)關(guān)鍵技術(shù)研究[D].北京：中國(guó)礦業(yè)大學(xué),，2017.

[6] ZHANG J L，WU Q,，DING Y P,，et al.Techniques for design and implementation of an FPGA-specific physical unclonable function[J].Journal of Computer Science and Technology，2016，31(1)：124-136.

[7] GANJI F,，TAJIK S,，SEIFERT J P，et al.Let me prove it to you：RO PUFs are provably learnable[M].Information Security and Cryptology-ICISC 2015.Springer International Publishing,，2015.

[8] ULRICH R,，SEHNKE F，SOLTER J,，et al.Modeling attacks on physical unclonable functions[J].CCS,，2010：237-249.

[9] CHANG H，SAPATNEKAR S.Statistical timing analysis considering spatial correlation in a pert-like traversal[C].International Conference on Computer Aided Design,，2003：621-625.

[10] 周志華.機(jī)器學(xué)習(xí)[M].北京：清華大學(xué)出版社,，2016.

[11] IAN GOODFELLOW H J，BENGIO Y,，COURVILLE A.Deep learning[J].Genetic Programming and Evolvable Machines,，2017：s10710-017-9314-z.

[12] 鄧生雄，雒江濤.集成隨機(jī)森林的分類模型[J].計(jì)算機(jī)應(yīng)用研究,，2015,，32(6)：1621-1624.

[13] 趙錦陽(yáng)，盧會(huì)國(guó),，蔣娟萍,，等.一種非平衡數(shù)據(jù)分類的過(guò)采樣隨機(jī)森林算法[J].計(jì)算機(jī)應(yīng)用與軟件，2019(4)：255-261,，316.

作者信息:

徐金甫,，董永興，李軍偉

(解放軍信息工程大學(xué),，河南 鄭州450001)