激活函數(shù)對神經(jīng)網(wǎng)絡(luò)的重要性自不必多言,,機器之心也曾發(fā)布過一些相關(guān)的介紹文章,,比如《一文概覽深度學(xué)習(xí)中的激活函數(shù)》,。本文同樣關(guān)注的是激活函數(shù),。來自丹麥技術(shù)大學(xué)的 Casper Hansen 通過公式,、圖表和代碼實驗介紹了 sigmoid,、ReLU、ELU 以及更新的 Leaky ReLU,、SELU、GELU 這些激活函數(shù),并比較了它們的優(yōu)勢和短板,。

在計算每一層的激活值時,,我們要用到激活函數(shù),之后才能確定這些激活值究竟是多少,。根據(jù)每一層前面的激活,、權(quán)重和偏置,我們要為下一層的每個激活計算一個值,。但在將該值發(fā)送給下一層之前,,我們要使用一個激活函數(shù)對這個輸出進行縮放。本文將介紹不同的激活函數(shù),。
在閱讀本文之前,,你可以閱讀我前一篇介紹神經(jīng)網(wǎng)絡(luò)中前向傳播和反向傳播的文章,其中已經(jīng)簡單地提及過激活函數(shù),,但還未介紹其實際所做的事情,。本文的內(nèi)容將建立在你已了解前一篇文章知識的基礎(chǔ)上。
前一篇文章地址:https://mlfromscratch.com/neural-networks-explained/
Casper Hansen
目錄
概述
sigmoid 函數(shù)是什么,?
梯度問題:反向傳播
梯度消失問題
梯度爆炸問題
梯度爆炸的極端案例
避免梯度爆炸:梯度裁剪/范數(shù)
整流線性單元(ReLU)
死亡 ReLU:優(yōu)勢和缺點
指數(shù)線性單元(ELU)
滲漏型整流線性單元(Leaky ReLU)
擴展型指數(shù)線性單元(SELU)
SELU:歸一化的特例
權(quán)重初始化+dropout
高斯誤差線性單元(GELU)
代碼:深度神經(jīng)網(wǎng)絡(luò)的超參數(shù)搜索
擴展閱讀:書籍與論文
概述
激活函數(shù)是神經(jīng)網(wǎng)絡(luò)中一個至關(guān)重要的部分,。在這篇長文中,我將全面介紹六種不同的激活函數(shù),,并闡述它們各自的優(yōu)缺點,。我會給出激活函數(shù)的方程和微分方程,還會給出它們的圖示,。本文的目標(biāo)是以簡單的術(shù)語解釋這些方程以及圖,。

我會介紹梯度消失和爆炸問題;對于后者,,我將按照 Nielsen 提出的那個很贊的示例來解釋梯度爆炸的原因,。
最后,我還會提供一些代碼讓你可以自己在 Jupyter Notebook 中運行,。
我會在 MNIST 數(shù)據(jù)集上進行一些小型代碼實驗,,為每個激活函數(shù)都獲得一張損失和準確度圖。
sigmoid 函數(shù)是什么,?
sigmoid 函數(shù)是一個 logistic 函數(shù),,意思就是說:不管輸入是什么,得到的輸出都在 0 到 1 之間,。也就是說,,你輸入的每個神經(jīng)元、節(jié)點或激活都會被縮放為一個介于 0 到 1 之間的值,。
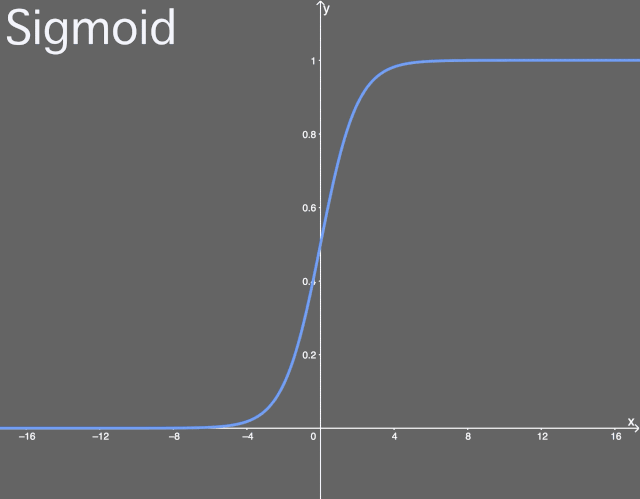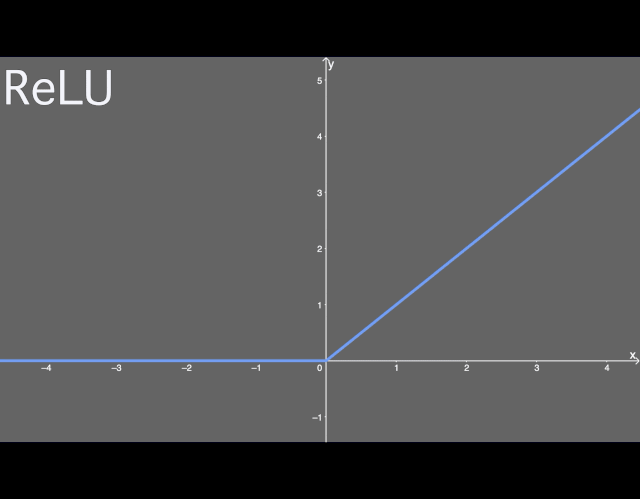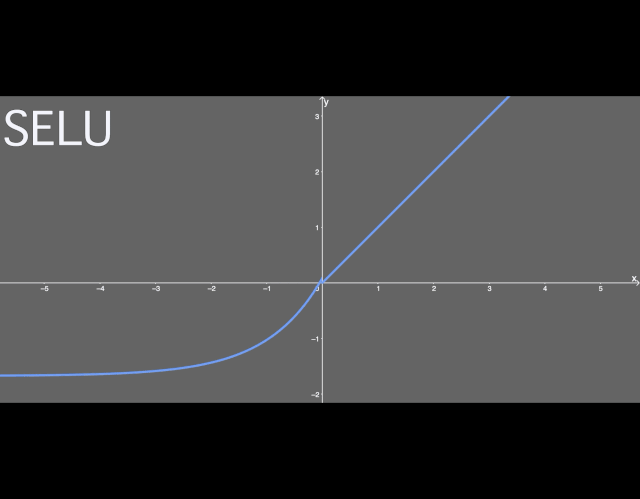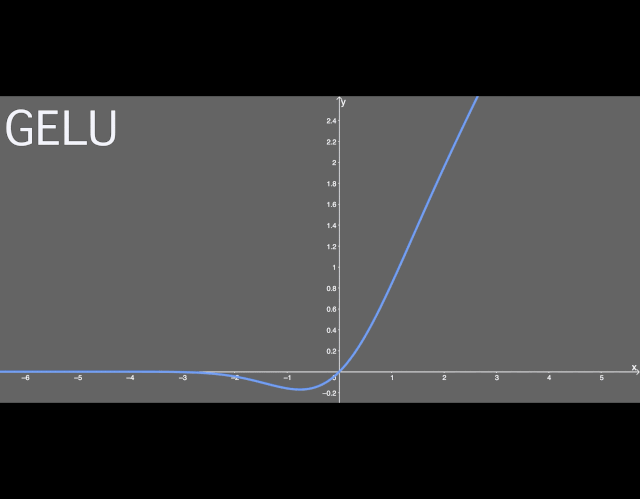
sigmoid 函數(shù)圖示,。
sigmoid 這樣的函數(shù)常被稱為非線性函數(shù),因為我們不能用線性的項來描述它。很多激活函數(shù)都是非線性或者線性和非線性的組合(有可能函數(shù)的一部分是線性的,,但這種情況很少見),。
這基本上沒什么問題,但值恰好為 0 或 1 的時候除外(有時候確實會發(fā)生這種情況),。為什么這會有問題,?
這個問題與反向傳播有關(guān)(有關(guān)反向傳播的介紹請參閱我的前一篇文章)。在反向傳播中,,我們要計算每個權(quán)重的梯度,,即針對每個權(quán)重的小更新。這樣做的目的是優(yōu)化整個網(wǎng)絡(luò)中激活值的輸出,,使其能在輸出層得到更好的結(jié)果,,進而實現(xiàn)對成本函數(shù)的優(yōu)化。
在反向傳播過程中,,我們必須計算每個權(quán)重影響成本函數(shù)(cost function)的比例,,具體做法是計算成本函數(shù)相對于每個權(quán)重的偏導(dǎo)數(shù)。假設(shè)我們不定義單個的權(quán)重,,而是將最后一層 L 中的所有權(quán)重 w 定義為 w^L,,則它們的導(dǎo)數(shù)為:
注意,當(dāng)求偏導(dǎo)數(shù)時,,我們要找到 ?a^L 的方程,,然后僅微分 ?z^L,其余部分保持不變,。我們用撇號「'」來表示任意函數(shù)的導(dǎo)數(shù),。當(dāng)計算中間項 ?a^L/?z^L 的偏導(dǎo)數(shù)時,我們有:
則 sigmoid 函數(shù)的導(dǎo)數(shù)就為:
當(dāng)我們向這個 sigmoid 函數(shù)輸入一個很大的 x 值(正或負)時,,我們得到幾乎為 0 的 y 值——也就是說,,當(dāng)我們輸入 w×a+b 時,我們可能得到一個接近于 0 的值,。

sigmoid 函數(shù)的導(dǎo)數(shù)圖示,。
當(dāng) x 是一個很大的值(正或負)時,我們本質(zhì)上就是用一個幾乎為 0 的值來乘這個偏導(dǎo)數(shù)的其余部分,。
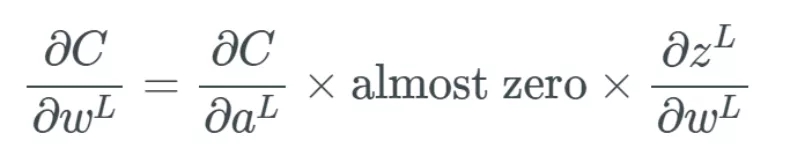
如果有太多的權(quán)重都有這樣很大的值,,那么我們根本就沒法得到可以調(diào)整權(quán)重的網(wǎng)絡(luò),這可是個大問題,。如果我們不調(diào)整這些權(quán)重,,那么網(wǎng)絡(luò)就只有細微的更新,這樣算法就不能隨時間給網(wǎng)絡(luò)帶來多少改善,。對于針對一個權(quán)重的偏導(dǎo)數(shù)的每個計算,,我們都將其放入一個梯度向量中,,而且我們將使用這個梯度向量來更新神經(jīng)網(wǎng)絡(luò)??梢韵胂?,如果該梯度向量的所有值都接近 0,,那么我們根本就無法真正更新任何東西,。

這里描述的就是梯度消失問題。這個問題使得 sigmoid 函數(shù)在神經(jīng)網(wǎng)絡(luò)中并不實用,,我們應(yīng)該使用后面介紹的其它激活函數(shù),。
梯度問題
梯度消失問題
我的前一篇文章說過,如果我們想更新特定的權(quán)重,,則更新規(guī)則為:

但如果偏導(dǎo)數(shù) ?C/?w^(L) 很小,,如同消失了一般,又該如何呢,?這時我們就遇到了梯度消失問題,,其中許多權(quán)重和偏置只能收到非常小的更新。

可以看到,,如果權(quán)重的值為 0.2,,則當(dāng)出現(xiàn)梯度消失問題時,這個值基本不會變化,。因為這個權(quán)重分別連接了第一層和第二層的首個神經(jīng)元,,所以我們可以用的表示方式將其記為

假設(shè)這個權(quán)重的值為 0.2,給定一個學(xué)習(xí)率(具體多少不重要,,這里使用了 0.5),,則新的權(quán)重為:
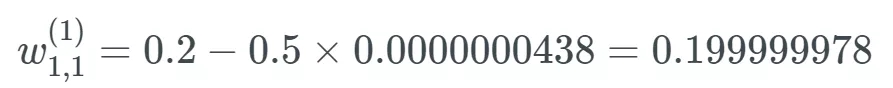
這個權(quán)重原來的值為 0.2,現(xiàn)在更新為了 0.199999978,。很明顯,,這是有問題的:梯度很小,如同消失了一樣,,使得神經(jīng)網(wǎng)絡(luò)中的權(quán)重幾乎沒有更新,。這會導(dǎo)致網(wǎng)絡(luò)中的節(jié)點離其最優(yōu)值相去甚遠。這個問題會嚴重妨礙神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí),。
人們已經(jīng)觀察到,,如果不同層的學(xué)習(xí)速度不同,那么這個問題還會變得更加嚴重,。層以不同的速度學(xué)習(xí),,前面幾層總是會根據(jù)學(xué)習(xí)率而變得更差。
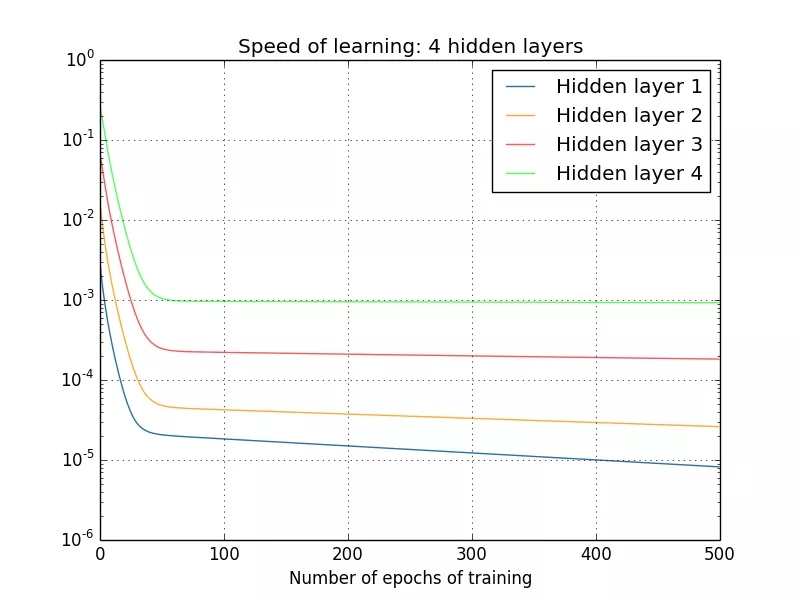
出自 Nielsen 的書《Neural Networks and Deep Learning》,。
在這個示例中,,隱藏層 4 的學(xué)習(xí)速度最快,,因為其成本函數(shù)僅取決于連接到隱藏層 4 的權(quán)重變化。我們看看隱藏層 1,;這里的成本函數(shù)取決于連接隱藏層 1 與隱藏層 2,、3、4 的權(quán)重變化,。如果你看過了我前一篇文章中關(guān)于反向傳播的內(nèi)容,,那么你可能知道網(wǎng)絡(luò)中更前面的層會復(fù)用后面層的計算。
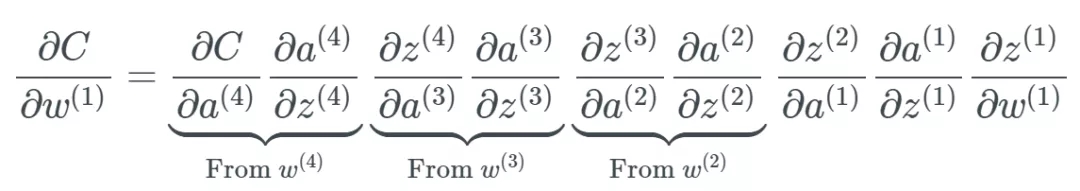
同時,,如前面介紹的那樣,,最后一層僅取決于計算偏導(dǎo)時出現(xiàn)的一組變化:
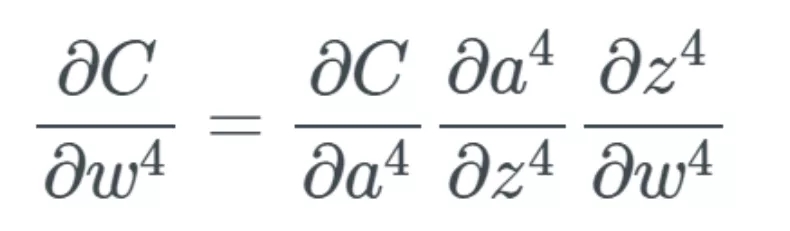
最終,這就是個大問題了,,因為現(xiàn)在權(quán)重層的學(xué)習(xí)速度不同,。這意味著網(wǎng)絡(luò)中更后面的層幾乎肯定會被網(wǎng)絡(luò)中更前面的層受到更多優(yōu)化。
而且問題還在于反向傳播算法不知道應(yīng)該向哪個方向傳遞權(quán)重來優(yōu)化成本函數(shù),。
梯度爆炸問題
梯度爆炸問題本質(zhì)上就是梯度消失問題的反面,。研究表明,這樣的問題是可能出現(xiàn)的,,這時權(quán)重處于「爆炸」?fàn)顟B(tài),,即它們的值快速增長。
我們將遵照以下示例來進行說明:
http://neuralnetworksanddeeplearning.com/chap5.html#what's_causing_the_vanishing_gradient_problem_unstable_gradients_in_deep_neural_nets
注意,,這個示例也可用于展示梯度消失問題,,而我是從更概念的角度選擇了它,以便更輕松地解釋,。
本質(zhì)上講,,當(dāng) 0<w<1 時,我們可能遇到梯度消失問題,;當(dāng) w>1 時,,我們可能遇到梯度爆炸問題。但是,,當(dāng)一個層遇到這個問題時,,必然有更多權(quán)重滿足梯度消失或爆炸的條件。
我們從一個簡單網(wǎng)絡(luò)開始,。這個網(wǎng)絡(luò)有少量權(quán)重,、偏置和激活,而且每一層也只有一個節(jié)點,。

這個網(wǎng)絡(luò)很簡單,。權(quán)重表示為 w_j,偏置為 b_j,,成本函數(shù)為 C,。節(jié)點,、神經(jīng)元或激活表示為圓圈。
Nielsen 使用了物理學(xué)上的常用表示方式 Δ 來描述某個值中的變化(這不同于梯度符號 ?),。舉個例子,,Δb_j 描述的是第 j 個偏置的值變化。
我前一篇文章的核心是我們要衡量與成本函數(shù)有關(guān)的權(quán)重和偏置的變化率,。先不考慮層,,我們看看一個特定的偏置,即第一個偏置 b_1,。然后我們通過下式衡量變化率:

下面式子的論據(jù)和上面的偏導(dǎo)一樣,。即我們?nèi)绾瓮ㄟ^偏置的變化率來衡量成本函數(shù)的變化率?正如剛才介紹的那樣,,Nielsen 使用 Δ 來描述變化,因此我們可以說這個偏導(dǎo)能大致通過 Δ 來替代:

權(quán)重和偏置的變化可以進行如下可視化:
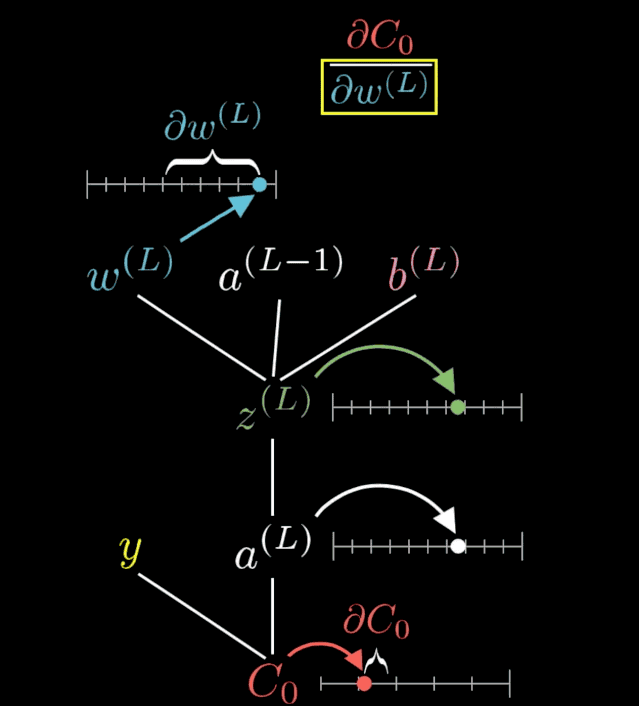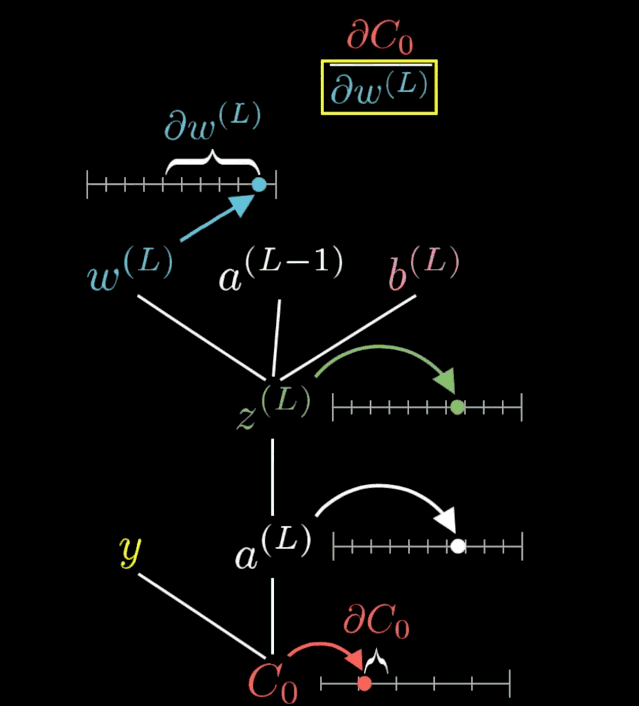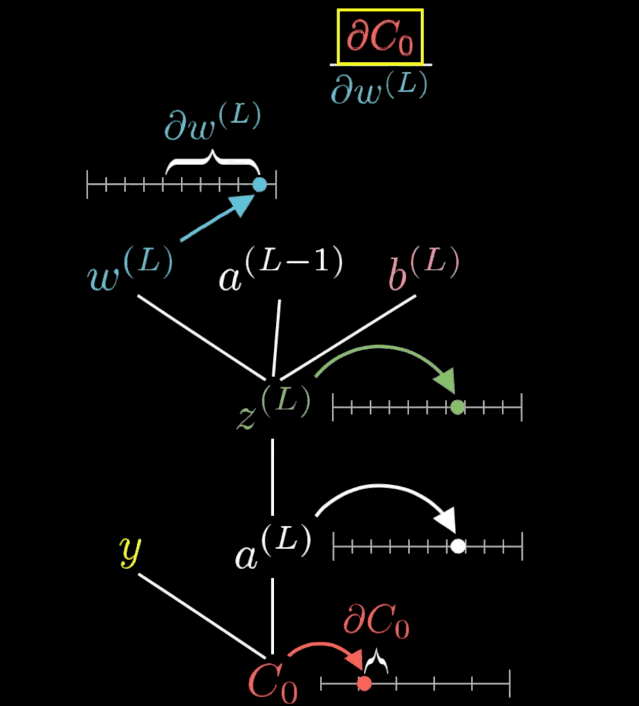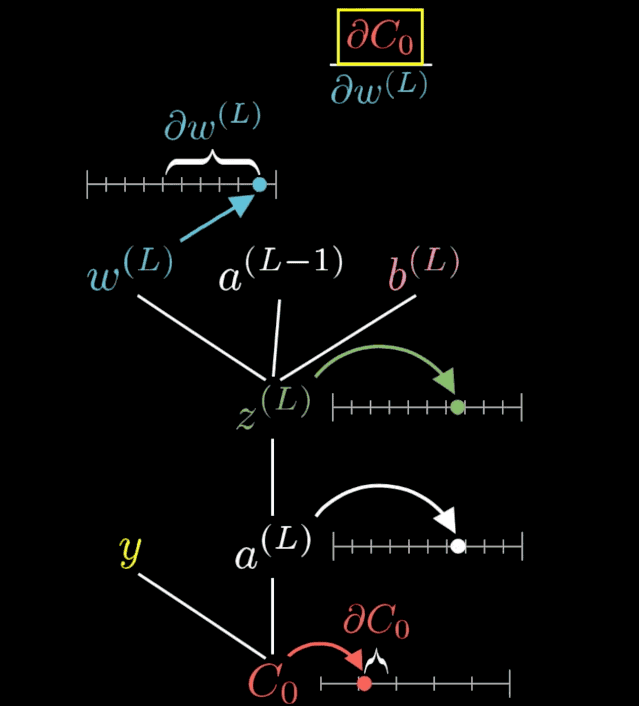
動圖出自 3blue1brown,,視頻地址:https://www.youtube.com/watch?v=tIeHLnjs5U8,。
我們先從網(wǎng)絡(luò)的起點開始,計算第一個偏置 b_1 中的變化將如何影響網(wǎng)絡(luò),。因為我們知道,,在上一篇文章中,第一個偏置 b_1 會饋入第一個激活 a_1,,我們就從這里開始,。我們先回顧一下這個等式:
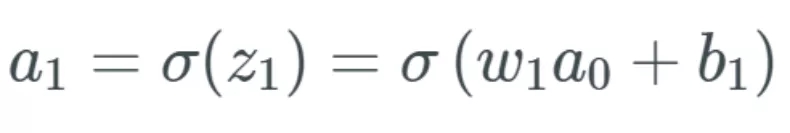
如果 b_1 改變,我們將這個改變量表示為 Δb_1,。因此,,我們注意到當(dāng) b_1 改變時,激活 a_1 也會改變——我們通常將其表示為 ?a_1/?b_1,。
因此,,我們左邊有偏導(dǎo)的表達式,這是 b_1 中與 a_1 相關(guān)的變化,。但我們開始替換左邊的項,,先用 z_1 的 sigmoid 替換 a_1:
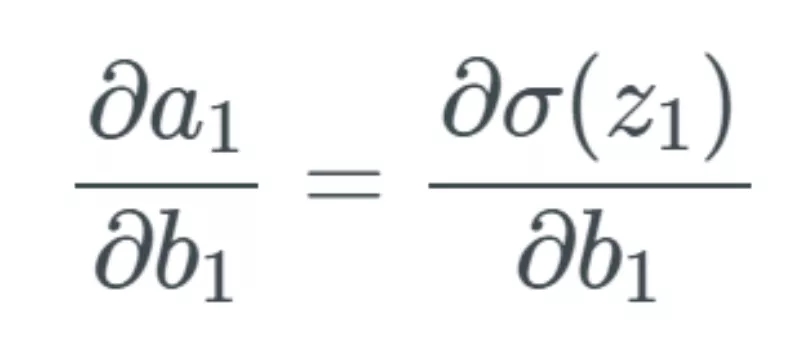
上式表示當(dāng) b_1 變化時,激活值 a_1 中存在某個變化,。我們將這個變化描述為 Δa_1,。
我們將變化 Δa_1 看作是與激活值 a_1 中的變化加上變化 Δb_1 近似一樣。
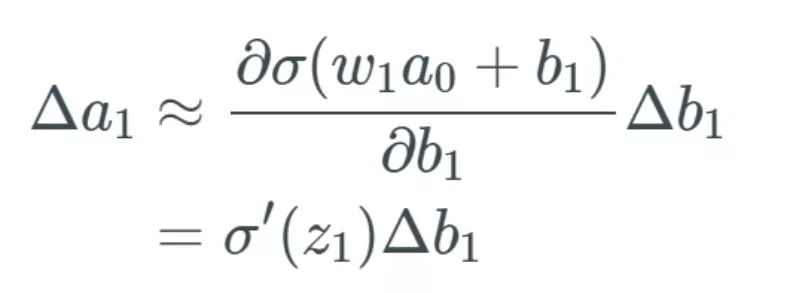
這里我們跳過了一步,,但本質(zhì)上講,,我們只是計算了偏導(dǎo)數(shù),并用偏導(dǎo)的結(jié)果替代了分數(shù)部分,。
a_1 的變化導(dǎo)致 z_2 的變化
所描述的變化 Δa_1 現(xiàn)在會導(dǎo)致下一層的輸入 z_2 出現(xiàn)變化,。如果這看起來很奇怪或者你還不信服,,我建議你閱讀我的前一篇文章。
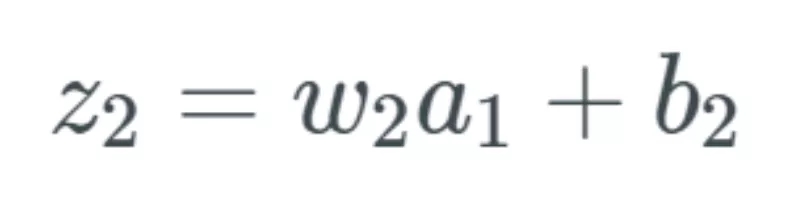
表示方式和前面一樣,,我們將下一個變化記為 Δz_2,。我們又要再次經(jīng)歷前面的過程,只是這次要得到的是 z_2 中的變化:
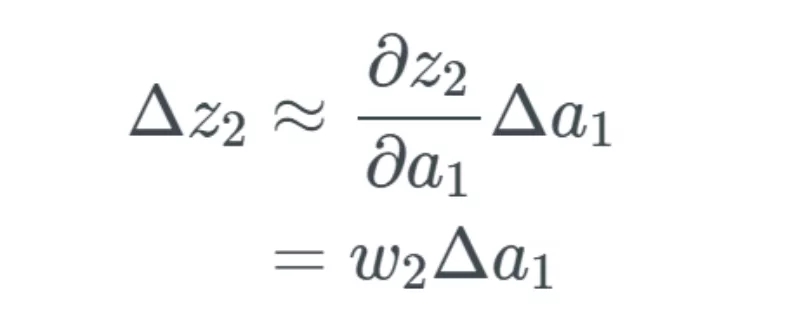
我們可以使用下式替代 Δa_1:

我們只計算這個式子,。希望你清楚地明白到這一步的過程——這與計算 Δa_1 的過程一樣,。
這個過程會不斷重復(fù),直到我們計算完整個網(wǎng)絡(luò),。通過替換 Δa_j 值,,我們得到一個最終函數(shù),其計算的是成本函數(shù)中與整個網(wǎng)絡(luò)(即所有權(quán)重,、偏置和激活)相關(guān)的變化,。
基于此,我們再計算 ?C/?b_1,,得到我們需要的最終式:
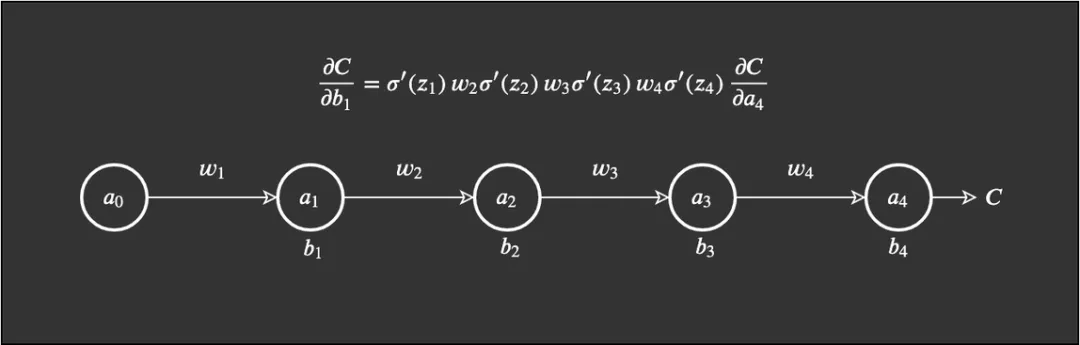
梯度爆炸的極端案例
據(jù)此,,如果所有權(quán)重 w_j 都很大,即如果很多權(quán)重的值大于 1,,我們就會開始乘以較大的值,。舉個例子,所有權(quán)重都有一些非常高的值,,比如 100,,而我們得到一些在 0 到 0.25 之間、 sigmoid 函數(shù)導(dǎo)數(shù)的隨機輸出:
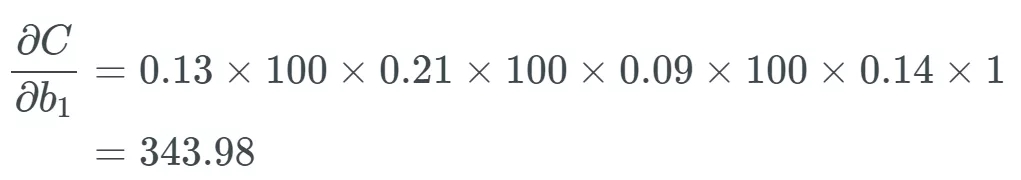
最后一個偏導(dǎo)為,,可以合理地相信這會遠大于 1,,但為了方便示例展示,我們將其設(shè)為 1,。
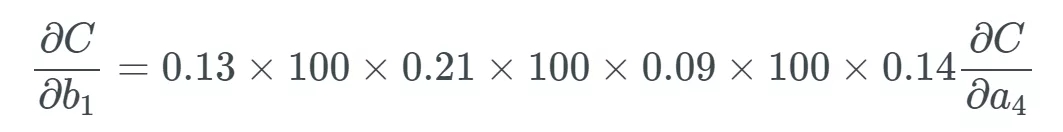
使用這個更新規(guī)則,,如果我們假設(shè) b_1 之前等于 1.56,而學(xué)習(xí)率等于 0.5,。

盡管這是一個極端案例,,但你懂我的意思。權(quán)重和偏置的值可能會爆發(fā)式地增大,,進而導(dǎo)致整個網(wǎng)絡(luò)爆炸,。
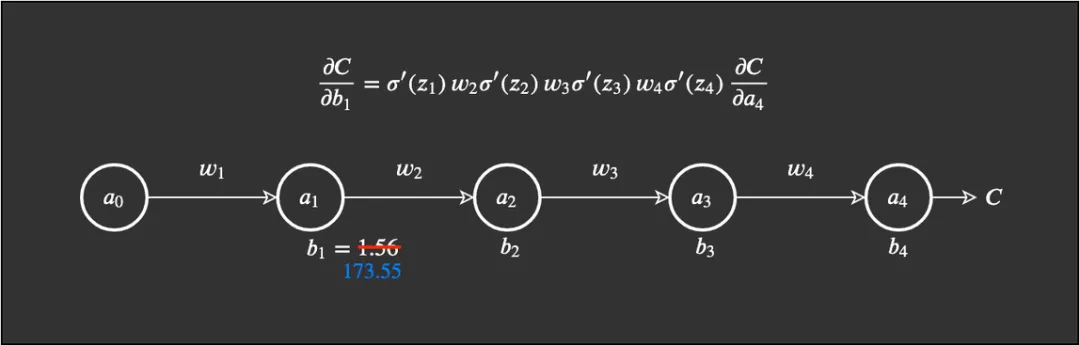
現(xiàn)在花點時間想想網(wǎng)絡(luò)的權(quán)重和偏置以及激活的其它部分,爆炸式地更新它們的值,。這就是我們所說的梯度爆炸問題,。很顯然,這樣的網(wǎng)絡(luò)學(xué)不到什么東西,,因此這會完全毀掉你想要解決的任務(wù),。
避免梯度爆炸:梯度裁剪/規(guī)范
解決梯度爆炸問題的基本思路就是為其設(shè)定一個規(guī)則,。這部分我不會深入進行數(shù)學(xué)解釋,但我會給出這個過程的步驟:
選取一個閾值——如果梯度超過這個值,,則使用梯度裁剪或梯度規(guī)范,;
定義是否使用梯度裁剪或規(guī)范。如果使用梯度裁剪,,你就指定一個閾值,,比如 0.5。如果這個梯度值超過 0.5 或 -0.5,,則要么通過梯度規(guī)范化將其縮放到閾值范圍內(nèi),,要么就將其裁剪到閾值范圍內(nèi)。
但是要注意,,這些梯度方法都不能避免梯度消失問題,。所以我們還將進一步探索解決這個問題的更多方法。通常而言,,如果你在使用循環(huán)神經(jīng)網(wǎng)絡(luò)架構(gòu)(比如 LSTM 或 GRU),,那么你就需要這些方法,因為這種架構(gòu)常出現(xiàn)梯度爆炸的情況,。
整流線性單元(ReLU)
整流線性單元是我們解決梯度消失問題的方法,但這是否會導(dǎo)致其它問題呢,?請往下看,。
ReLU 的公式如下:

ReLU 公式表明:
如果輸入 x 小于 0,則令輸出等于 0,;
如果輸入 x 大于 0,,則令輸出等于輸入。
盡管我們沒法用大多數(shù)工具繪制其圖形,,但你可以這樣用圖解釋 ReLU,。x 值小于零的一切都映射為 0 的 y 值,但 x 值大于零的一切都映射為它本身,。也就是說,,如果我們輸入 x=1,我們得到 y=1,。
ReLU 激活函數(shù)圖示,。
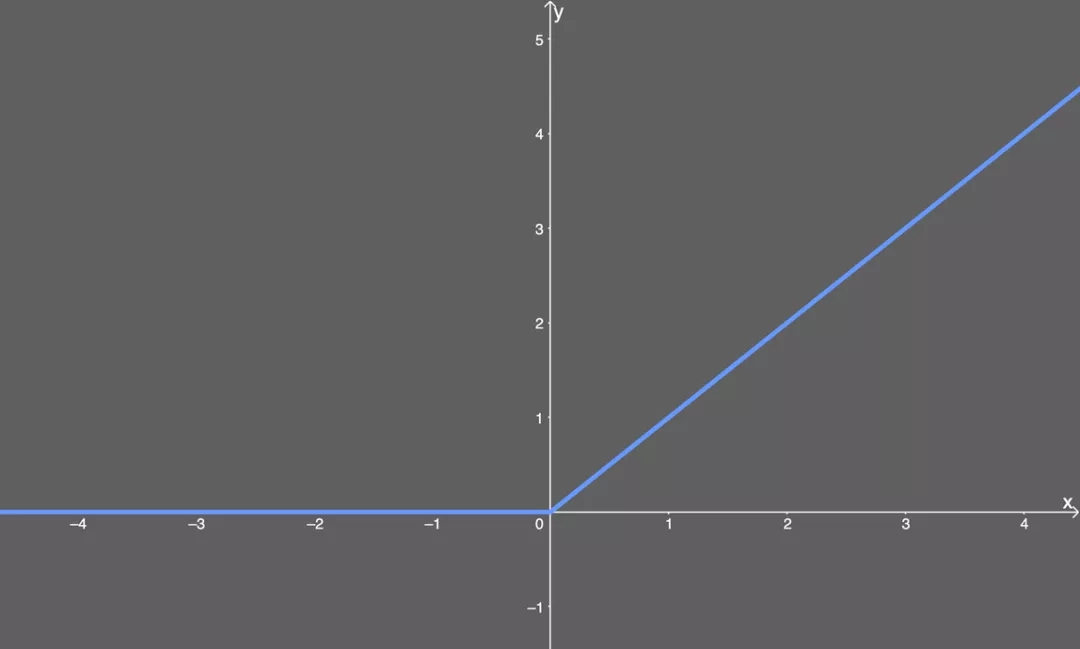
這很好,但這與梯度消失問題有什么關(guān)系,?首先,,我們必須得到其微分方程:
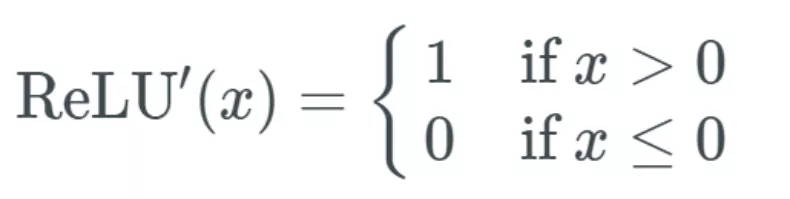
其意思是:
如果輸入 x 大于 0,則輸出等于 1,;
如果輸入小于或等于 0,,則輸出變?yōu)?0,。
用下圖表示:
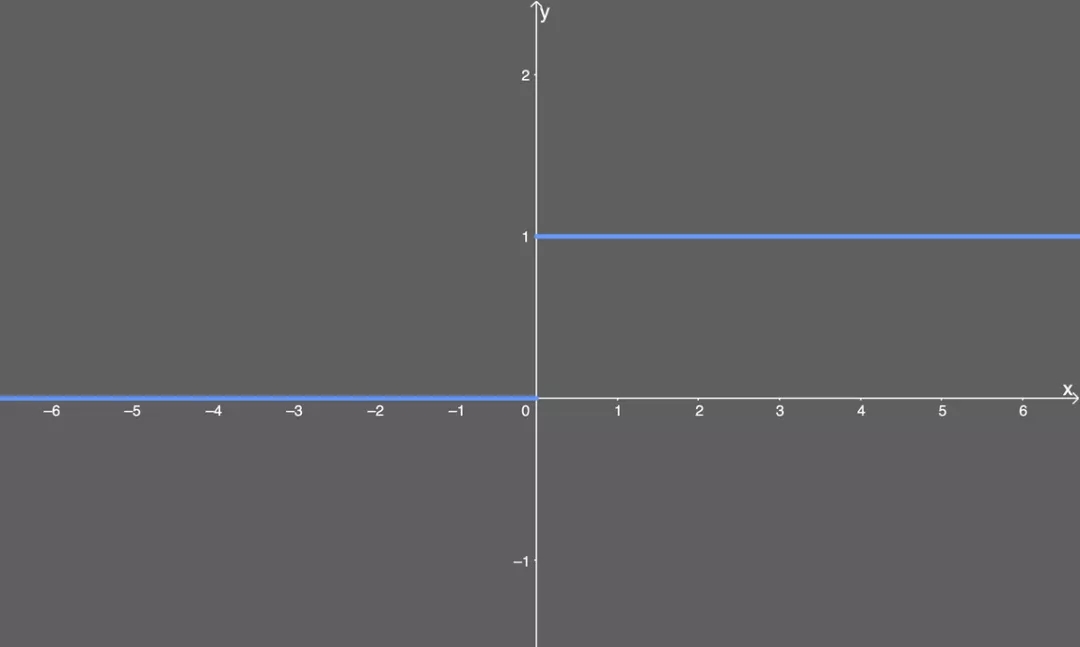
已微分的 ReLU。
現(xiàn)在我們得到了答案:當(dāng)使用 ReLU 激活函數(shù)時,,我們不會得到非常小的值(比如前面 sigmoid 函數(shù)的 0.0000000438),。相反,它要么是 0(導(dǎo)致某些梯度不返回任何東西),,要么是 1,。
但這又催生出另一個問題:死亡 ReLU 問題。
如果在計算梯度時有太多值都低于 0 會怎樣呢,?我們會得到相當(dāng)多不會更新的權(quán)重和偏置,,因為其更新的量為 0。要了解這個過程的實際表現(xiàn),,我們反向地看看前面梯度爆炸的示例,。
我們在這個等式中將 ReLU 記為 R,我們只需要將每個 sigmoid σ 替換成 R:
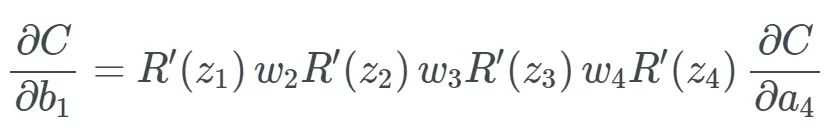
現(xiàn)在,,假如說這個微分后的 ReLU 的一個隨機輸入 z 小于 0——則這個函數(shù)會導(dǎo)致偏置「死亡」,。假設(shè)是 R'(z_3)=0:
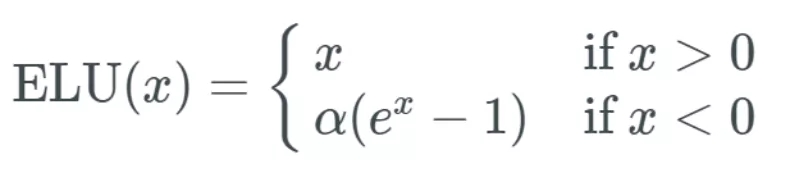
反過來,當(dāng)我們得到 R'(z_3)=0 時,,與其它值相乘自然也只能得到 0,,這會導(dǎo)致這個偏置死亡。我們知道一個偏置的新值是該偏置減去學(xué)習(xí)率減去梯度,,這意味著我們得到的更新為 0,。

死亡 ReLU:優(yōu)勢和缺點
當(dāng)我們將 ReLU 函數(shù)引入神經(jīng)網(wǎng)絡(luò)時,我們也引入了很大的稀疏性,。那么稀疏性這個術(shù)語究竟是什么意思,?
稀疏:數(shù)量少,通常分散在很大的區(qū)域,。在神經(jīng)網(wǎng)絡(luò)中,,這意味著激活的矩陣含有許多 0。這種稀疏性能讓我們得到什么,?當(dāng)某個比例(比如 50%)的激活飽和時,,我們就稱這個神經(jīng)網(wǎng)絡(luò)是稀疏的。這能提升時間和空間復(fù)雜度方面的效率——常數(shù)值(通常)所需空間更少,,計算成本也更低,。
Yoshua Bengio 等人發(fā)現(xiàn) ReLU 這種分量實際上能讓神經(jīng)網(wǎng)絡(luò)表現(xiàn)更好,而且還有前面提到的時間和空間方面的效率,。
論文地址:https://www.utc.fr/~bordesan/dokuwiki/_media/en/glorot10nipsworkshop.pdf
優(yōu)點:
相比于 sigmoid,,由于稀疏性,時間和空間復(fù)雜度更低;不涉及成本更高的指數(shù)運算,;
能避免梯度消失問題,。
缺點:
引入了死亡 ReLU 問題,即網(wǎng)絡(luò)的大部分分量都永遠不會更新,。但這有時候也是一個優(yōu)勢,;
ReLU 不能避免梯度爆炸問題。
指數(shù)線性單元(ELU)
指數(shù)線性單元激活函數(shù)解決了 ReLU 的一些問題,,同時也保留了一些好的方面,。這種激活函數(shù)要選取一個 α 值;常見的取值是在 0.1 到 0.3 之間,。
如果你數(shù)學(xué)不好,,ELU 的公式看起來會有些難以理解:
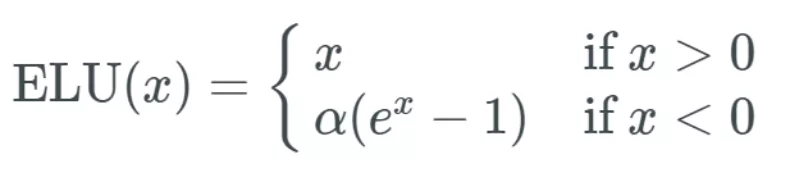
我解釋一下。如果你輸入的 x 值大于 0,,則結(jié)果與 ReLU 一樣——即 y 值等于 x 值,;但如果輸入的 x 值小于 0,則我們會得到一個稍微小于 0 的值,。
所得到的 y 值取決于輸入的 x 值,,但還要兼顧參數(shù) α——你可以根據(jù)需要來調(diào)整這個參數(shù)。更進一步,,我們引入了指數(shù)運算 e^x,,因此 ELU 的計算成本比 ReLU 高。
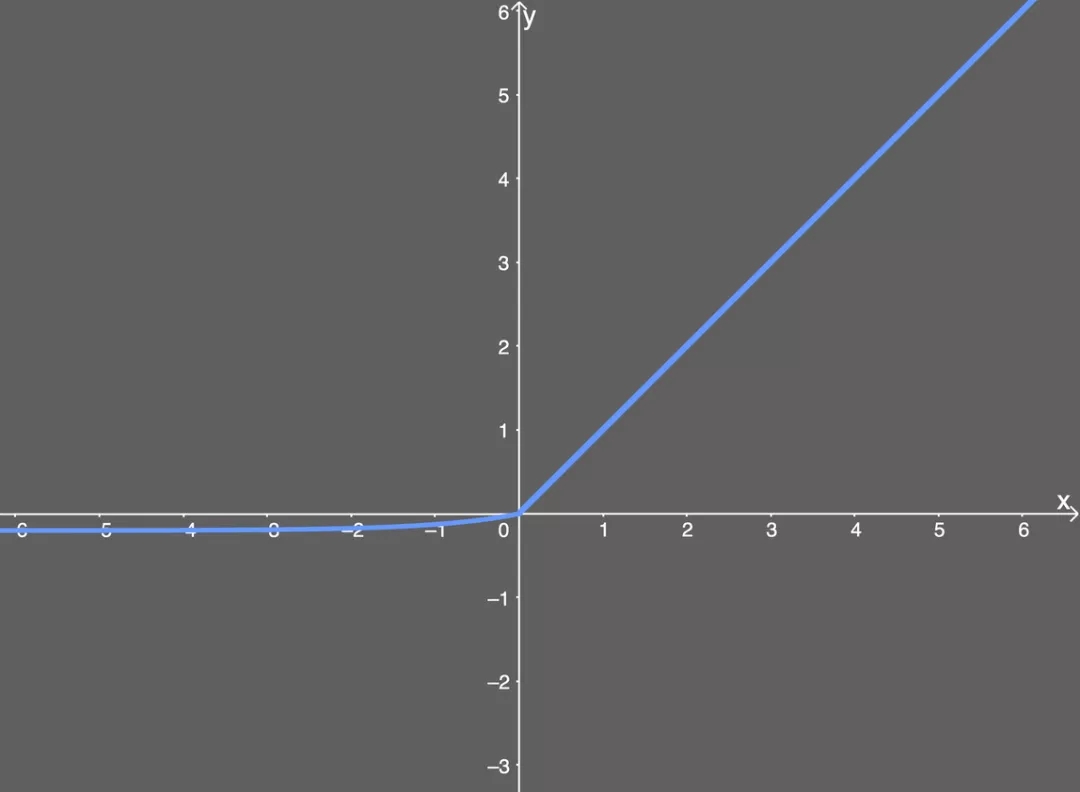
下面繪出了 α 值為 0.2 的 ELU 函數(shù)的圖:
ELU 激活函數(shù)圖示,。
上圖很直觀,,我們應(yīng)該還能很好地應(yīng)對梯度消失問題,因為輸入值沒有映射到非常小的輸出值,。
但 ELU 的導(dǎo)數(shù)又如何呢?這同樣也很重要,。
看起來很簡單,。如果輸入 x 大于 0,則 y 值輸出為 1,;如果輸入 x 小于或等于 0,,則輸出是 ELU 函數(shù)(未微分)加上 α 值。
可繪出圖為:

微分的 ELU 激活函數(shù),。
你可能已經(jīng)注意到,,這里成功避開了死亡 ReLU 問題,同時仍保有 ReLU 激活函數(shù)的一些計算速度增益——也就是說,,網(wǎng)絡(luò)中仍還有一些死亡的分量,。
優(yōu)點:
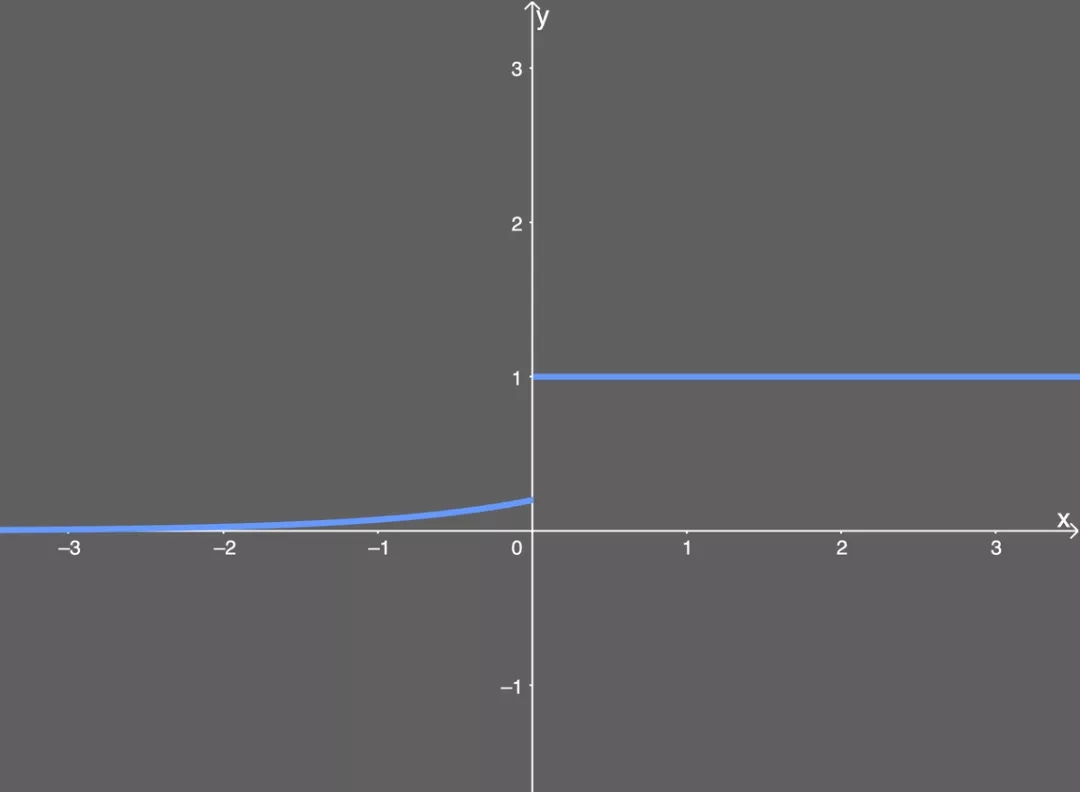
能避免死亡 ReLU 問題;
能得到負值輸出,這能幫助網(wǎng)絡(luò)向正確的方向推動權(quán)重和偏置變化,;
在計算梯度時能得到激活,,而不是讓它們等于 0。
缺點:
由于包含指數(shù)運算,,所以計算時間更長,;
無法避免梯度爆炸問題;
神經(jīng)網(wǎng)絡(luò)不學(xué)習(xí) α 值,。
滲漏型整流線性單元激活函數(shù)(Leaky ReLU)
滲漏型整流線性單元激活函數(shù)也有一個 α 值,,通常取值在 0.1 到 0.3 之間。Leaky ReLU 激活函數(shù)很常用,,但相比于 ELU 它也有一些缺陷,,但也比 ReLU 具有一些優(yōu)勢。
Leaky ReLU 的數(shù)學(xué)形式如下:
因此,,如果輸入 x 大于 0,,則輸出為 x;如果輸入 x 小于或等于 0,,則輸出為 α 乘以輸入,。
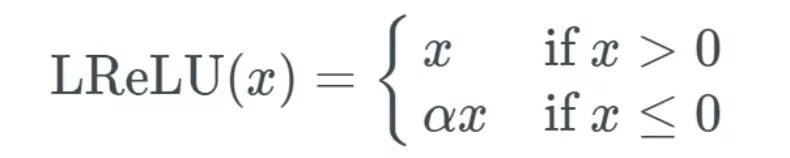
這意味著能夠解決死亡 ReLU 問題,因為梯度的值不再被限定為 0——另外,,這個函數(shù)也能避免梯度消失問題,。盡管梯度爆炸的問題依然存在,但后面的代碼部分會介紹如何解決,。
下面給出了 Leaky ReLU 的圖示,,其中假設(shè) α 值為 0.2:
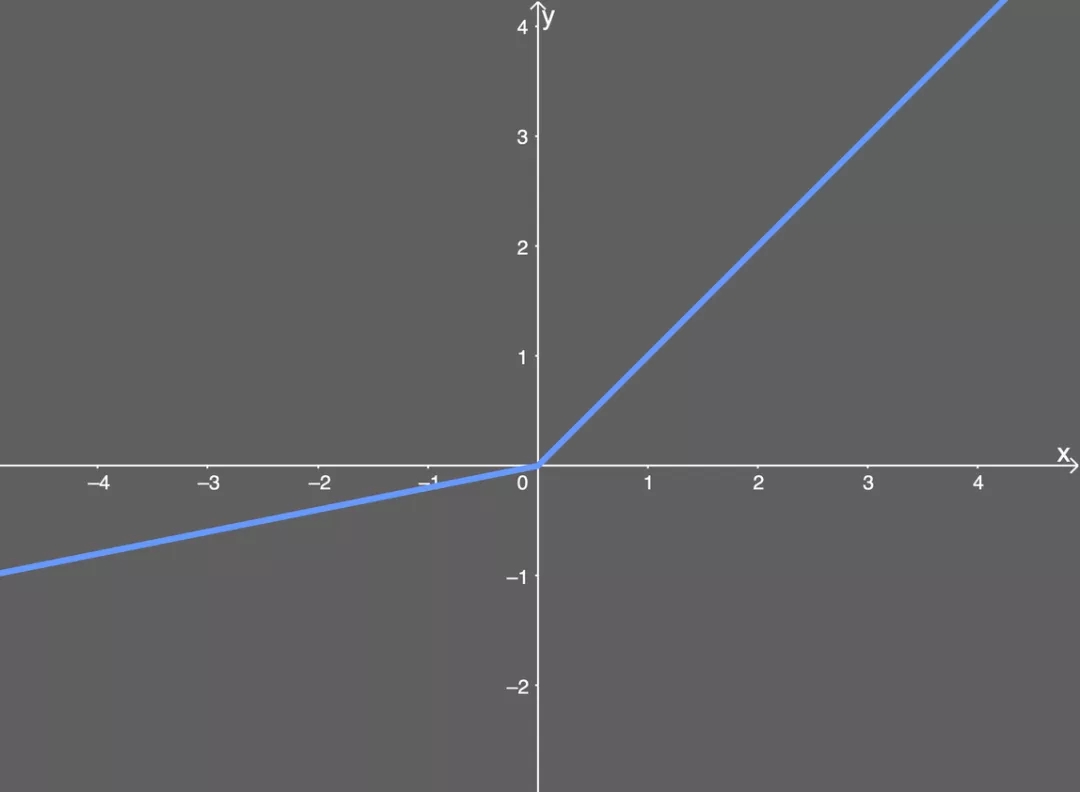
Leaky ReLU 圖示。
和在公式中看到的一樣,,如果 x 值大于 0,,則任意 x 值都映射為同樣的 y 值;但如果 x 值小于 0,,則會多一個系數(shù) 0.2,。也就是說,如果輸入值 x 為 -5,,則映射的輸出值為 -1,。
因為 Leaky ReLU 函數(shù)是兩個線性部分組合起來的,所以它的導(dǎo)數(shù)很簡單:

第一部分線性是當(dāng) x 大于 0 時,,輸出為 1,;而當(dāng)輸入小于 0 時,輸出就為 α 值,,這里我們選擇的是 0.2,。
微分的 Leaky ReLU 圖示,。

從上圖中也能明顯地看出來,輸入 x 大于或小于 0,,微分的 Leaky ReLU 各為一個常量,。
優(yōu)點:
類似 ELU,Leaky ReLU 也能避免死亡 ReLU 問題,,因為其在計算導(dǎo)數(shù)時允許較小的梯度,;
由于不包含指數(shù)運算,所以計算速度比 ELU 快,。
缺點:
無法避免梯度爆炸問題,;
神經(jīng)網(wǎng)絡(luò)不學(xué)習(xí) α 值;
在微分時,,兩部分都是線性的,;而 ELU 的一部分是線性的,一部分是非線性的,。
擴展型指數(shù)線性單元激活函數(shù)(SELU)
擴展型指數(shù)線性單元激活函數(shù)比較新,,介紹它的論文包含長達 90 頁的附錄(包括定理和證明等)。當(dāng)實際應(yīng)用這個激活函數(shù)時,,必須使用 lecun_normal 進行權(quán)重初始化,。如果希望應(yīng)用 dropout,則應(yīng)當(dāng)使用 AlphaDropout,。后面的代碼部分會更詳細地介紹,。
論文作者已經(jīng)計算出了公式的兩個值:α 和 λ;如下所示:

可以看到,,它們的小數(shù)點后還有很多位,,這是為了絕對精度。而且它們是預(yù)先確定的,,也就是說我們不必擔(dān)心如何為這個激活函數(shù)選取合適的 α 值,。
說實話,這個公式看起來和其它公式或多或少有些類似,。所有新的激活函數(shù)看起來就像是其它已有的激活函數(shù)的組合,。
SELU 的公式如下:

也就是說,如果輸入值 x 大于 0,,則輸出值為 x 乘以 λ;如果輸入值 x 小于 0,,則會得到一個奇異函數(shù)——它隨 x 增大而增大并趨近于 x 為 0 時的值 0.0848,。本質(zhì)上看,當(dāng) x 小于 0 時,,先用 α 乘以 x 值的指數(shù),,再減去 α,然后乘以 λ 值。
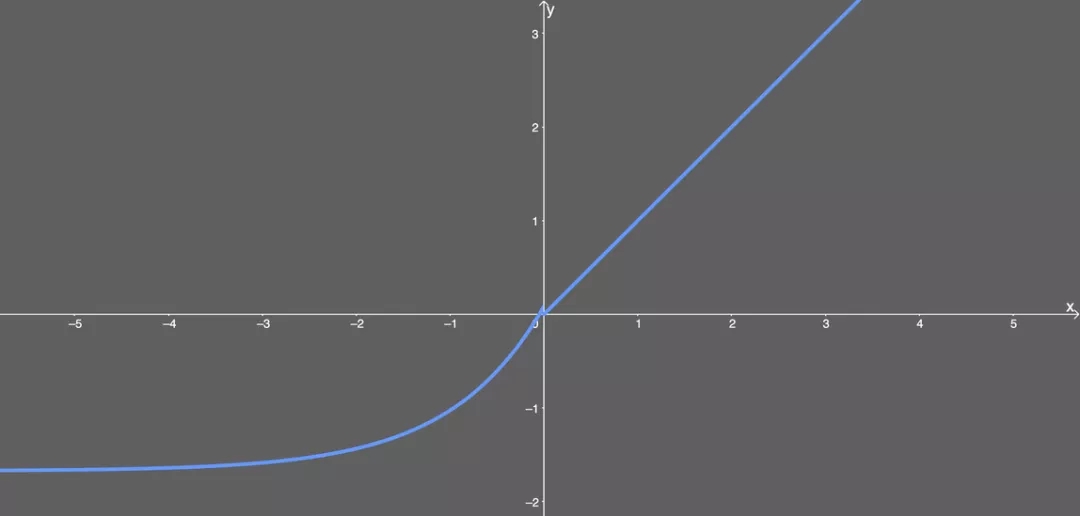
SELU 函數(shù)圖示,。
SELU 的特例
SELU 激活能夠?qū)ι窠?jīng)網(wǎng)絡(luò)進行自歸一化(self-normalizing),。這是什么意思?
首先,,我們先看看什么是歸一化(normalization),。簡單來說,歸一化首先是減去均值,,然后除以標(biāo)準差,。因此,經(jīng)過歸一化之后,,網(wǎng)絡(luò)的組件(權(quán)重,、偏置和激活)的均值為 0,標(biāo)準差為 1,。而這正是 SELU 激活函數(shù)的輸出值,。
均值為 0 且標(biāo)準差為 1 又如何呢?在初始化函數(shù)為 lecun_normal 的假設(shè)下,,網(wǎng)絡(luò)參數(shù)會被初始化一個正態(tài)分布(或高斯分布),,然后在 SELU 的情況下,網(wǎng)絡(luò)會在論文中描述的范圍內(nèi)完全地歸一化,。本質(zhì)上看,,當(dāng)乘或加這樣的網(wǎng)絡(luò)分量時,網(wǎng)絡(luò)仍被視為符合高斯分布,。我們就稱之為歸一化,。反過來,這又意味著整個網(wǎng)絡(luò)及其最后一層的輸出也是歸一化的,。
均值 μ 為 0 且標(biāo)準差 σ 為 1 的正態(tài)分布看起來是怎樣的,?
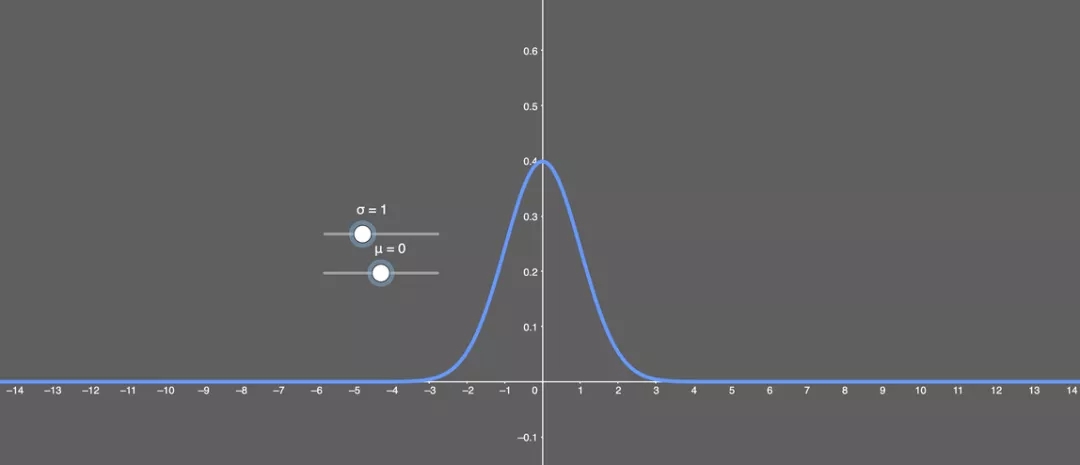
SELU 的輸出是歸一化的,這可稱為內(nèi)部歸一化(internal normalization),,因此事實上其所有輸出都是均值為 0 且標(biāo)準差為 1,。這不同于外部歸一化(external normalization)——會用到批歸一化或其它方法。
很好,,也就是說所有分量都會被歸一化,。但這是如何做到的?
簡單解釋一下,,當(dāng)輸入小于 0 時,,方差減小,;當(dāng)輸入大于 0 時,,方差增大——而標(biāo)準差是方差的平方根,,這樣我們就使得標(biāo)準差為 1。
我們通過梯度得到零均值,。我們需要一些正值和負值才能讓均值為 0,。我的上一篇文章介紹過,梯度可以調(diào)整神經(jīng)網(wǎng)絡(luò)的權(quán)重和偏置,,因此我們需要這些梯度輸出一些負值和正值,,這樣才能控制住均值。
均值 μ 和方差 ν 的主要作用是使我們有某個域 Ω,,讓我們總是能將均值和方差映射到預(yù)定義的區(qū)間內(nèi),。這些區(qū)間定義如下:
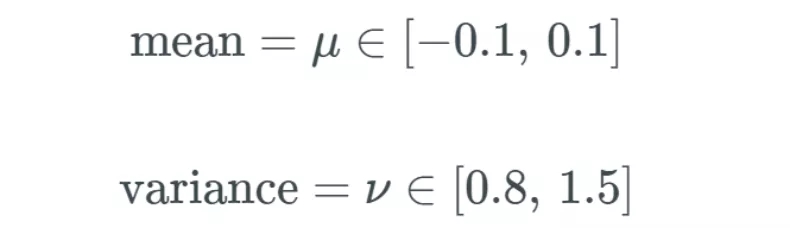
∈ 符號表示均值和方差在這些預(yù)定義的區(qū)間之內(nèi)。反過來,,這又能避免網(wǎng)絡(luò)出現(xiàn)梯度消失和爆炸問題,。
下面引述一段論文的解釋,說明了他們得到這個激活函數(shù)的方式,,我認為這很重要:
SELU 允許構(gòu)建一個映射 g,,其性質(zhì)能夠?qū)崿F(xiàn) SNN(自歸一化神經(jīng)網(wǎng)絡(luò))。SNN 不能通過(擴展型)修正線性單元(ReLU),、sigmoid 單元,、tanh 單元和 Leaky ReLU 實現(xiàn)。這個激活函數(shù)需要有:(1)負值和正值,,以便控制均值,;(2)飽和區(qū)域(導(dǎo)數(shù)趨近于零),以便抑制更低層中較大的方差,;(3)大于 1 的斜率,,以便在更低層中的方差過小時增大方差;(4)連續(xù)曲線,。后者能確保一個固定點,,其中方差抑制可通過方差增大來獲得均衡。我們能通過乘上指數(shù)線性單元(ELU)來滿足激活函數(shù)的這些性質(zhì),,而且 λ>1 能夠確保正值凈輸入的斜率大于 1,。
我們再看看 SELU 的微分函數(shù):
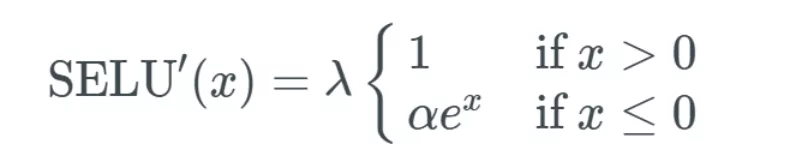
很好,不太復(fù)雜,,我們可以簡單地解釋一下,。如果 x 大于 0,則輸出值為 λ,;如果 x 小于 0,,則輸出為 α 乘以 x 的指數(shù)再乘 λ。
其圖形如下所示,,看起來很特別:
微分的 SELU 函數(shù),。
注意 SELU 函數(shù)也需要 lecun_normal 進行權(quán)重初始化;而且如果你想使用 dropout,,你也必須使用名為 Alpha Dropout 的特殊版本,。
優(yōu)點:
內(nèi)部歸一化的速度比外部歸一化快,這意味著網(wǎng)絡(luò)能更快收斂,;
不可能出現(xiàn)梯度消失或爆炸問題,,見 SELU 論文附錄的定理 2 和 3。
缺點:
這個激活函數(shù)相對較新——需要更多論文比較性地探索其在 CNN 和 RNN 等架構(gòu)中應(yīng)用,。
這里有一篇使用 SELU 的 CNN 論文:https://arxiv.org/pdf/1905.01338.pdf
GELU
高斯誤差線性單元激活函數(shù)在最近的 Transformer 模型(谷歌的 BERT 和 OpenAI 的 GPT-2)中得到了應(yīng)用,。GELU 的論文來自 2016 年,但直到最近才引起關(guān)注,。
這種激活函數(shù)的形式為:
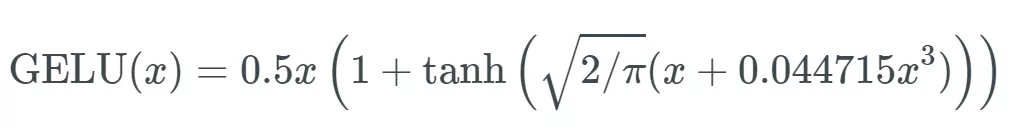
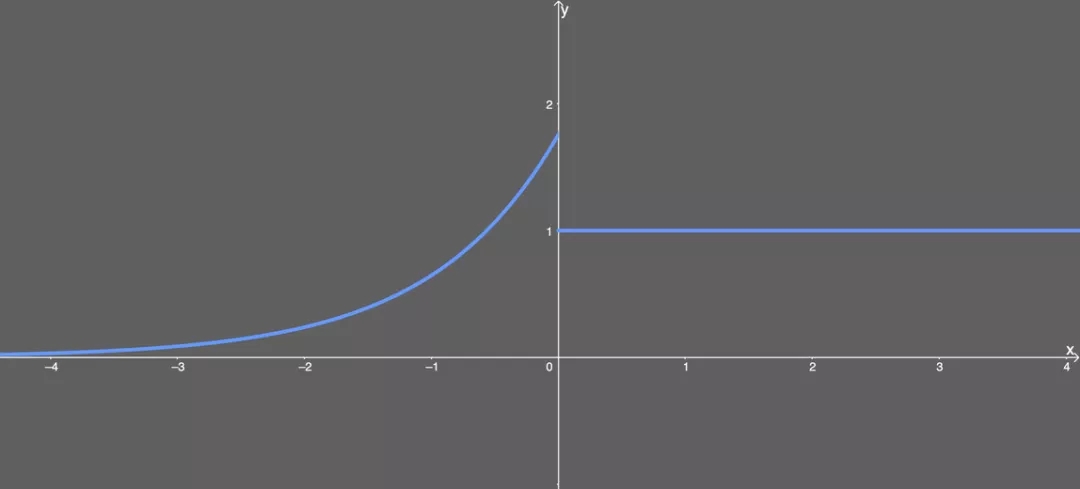
看得出來,,這就是某些函數(shù)(比如雙曲正切函數(shù) tanh)與近似數(shù)值的組合。沒什么過多可說的,。有意思的是這個函數(shù)的圖形:

GELU 激活函數(shù),。
可以看出,當(dāng) x 大于 0 時,,輸出為 x,;但 x=0 到 x=1 的區(qū)間除外,這時曲線更偏向于 y 軸,。
我沒能找到該函數(shù)的導(dǎo)數(shù),,所以我使用了 WolframAlpha 來微分這個函數(shù)。結(jié)果如下:

和前面一樣,,這也是雙曲函數(shù)的另一種組合形式,。但它的圖形看起來很有意思:

微分的 GELU 激活函數(shù)。
優(yōu)點:
似乎是 NLP 領(lǐng)域的當(dāng)前最佳,;尤其在 Transformer 模型中表現(xiàn)最好,;
能避免梯度消失問題。
缺點:
盡管是 2016 年提出的,,但在實際應(yīng)用中還是一個相當(dāng)新穎的激活函數(shù),。
用于深度神經(jīng)網(wǎng)絡(luò)的代碼
假如說你想要嘗試所有這些激活函數(shù),以便了解哪種最適合,,你該怎么做,?通常我們會執(zhí)行超參數(shù)優(yōu)化——這可以使用 scikit-learn 的 GridSearchCV 函數(shù)實現(xiàn)。但是我們想要進行比較,,所以我們的想法是選取一些超參數(shù)并讓它們保持恒定,,同時修改激活函數(shù)。
說明一下我這里要做的事情:
使用本文提及的激活函數(shù)訓(xùn)練同樣的神經(jīng)網(wǎng)絡(luò)模型,;
使用每個激活函數(shù)的歷史記錄,,繪制損失和準確度隨 epoch 的變化圖,。
本代碼也發(fā)布在了 GitHub 上,并且支持 colab,,以便你能夠快速運行,。地址:https://github.com/casperbh96/Activation-Functions-Search
我更偏好使用 Keras 的高級 API,所以這會用 Keras 來完成,。
首先導(dǎo)入我們所需的一切,。注意這里使用了 4 個庫:tensorflow、numpy,、matplotlib,、 keras。
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from keras.datasets import mnist
from keras.utils.np_utils import to_categorical
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten, Conv2D, MaxPooling2D, Activation, LeakyReLU
from keras.layers.noise import AlphaDropout
from keras.utils.generic_utils import get_custom_objects
from keras import backend as K
from keras.optimizers import Adam
現(xiàn)在加載我們運行實驗所需的數(shù)據(jù)集,;這里選擇了 MNIST 數(shù)據(jù)集,。我們可以直接從 Keras 導(dǎo)入它。
(x_train, y_train), (x_test, y_test) = mnist.load_data()
很好,,但我們想對數(shù)據(jù)進行一些預(yù)處理,,比如歸一化。我們需要通過很多函數(shù)來做這件事,,主要是調(diào)整圖像大?。?reshape)并除以最大的 RGB 值 255(/= 255)。最后,,我們通過 to_categorical() 對數(shù)據(jù)進行 one-hot 編碼,。
def preprocess_mnist(x_train, y_train, x_test, y_test):
# Normalizing all images of 28x28 pixels
x_train = x_train.reshape(x_train.shape[0], 28, 28, 1)
x_test = x_test.reshape(x_test.shape[0], 28, 28, 1)
input_shape = (28, 28, 1)
# Float values for division
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
# Normalizing the RGB codes by dividing it to the max RGB value
x_train /= 255
x_test /= 255
# Categorical y values
y_train = to_categorical(y_train)
y_test= to_categorical(y_test)
return x_train, y_train, x_test, y_test, input_shape
x_train, y_train, x_test, y_test, input_shape = preprocess_mnist(x_train, y_train, x_test, y_test)
現(xiàn)在我們已經(jīng)完成了數(shù)據(jù)預(yù)處理,可以構(gòu)建模型以及定義 Keras 運行所需的參數(shù)了,。首先從卷積神經(jīng)網(wǎng)絡(luò)模型本身開始,。SELU 激活函數(shù)是一個特殊情況,我們需要使用核初始化器 'lecun_normal' 和特殊形式的 dropout AlphaDropout(),,其它一切都保持常規(guī)設(shè)定,。
def build_cnn(activation,
dropout_rate,
optimizer):
model = Sequential()if(activation == 'selu'):
model.add(Conv2D(32, kernel_size=(3, 3),
activation=activation,
input_shape=input_shape,
kernel_initializer='lecun_normal'))
model.add(Conv2D(64, (3, 3), activation=activation,
kernel_initializer='lecun_normal'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(AlphaDropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation=activation,
kernel_initializer='lecun_normal'))
model.add(AlphaDropout(0.5))
model.add(Dense(10, activation='softmax'))else:
model.add(Conv2D(32, kernel_size=(3, 3),
activation=activation,
input_shape=input_shape))
model.add(Conv2D(64, (3, 3), activation=activation))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation=activation))
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax'))
model.compile(
loss='binary_crossentropy',
optimizer=optimizer,
metrics=['accuracy'])return model
使用 GELU 函數(shù)有個小問題;Keras 中目前還沒有這個函數(shù),。幸好我們能輕松地向 Keras 添加新的激活函數(shù),。
# Add the GELU function to Keras
def gelu(x):
return 0.5 * x * (1 + tf.tanh(tf.sqrt(2 / np.pi) * (x + 0.044715 * tf.pow(x, 3))))
get_custom_objects().update({'gelu': Activation(gelu)})
# Add leaky-relu so we can use it as a string
get_custom_objects().update({'leaky-relu': Activation(LeakyReLU(alpha=0.2))})
act_func = ['sigmoid', 'relu', 'elu', 'leaky-relu', 'selu', 'gelu']
現(xiàn)在我們可以使用 act_func 數(shù)組中定義的不同激活函數(shù)訓(xùn)練模型了。我們會在每個激活函數(shù)上運行一個簡單的 for 循環(huán),,并將結(jié)果添加到一個數(shù)組:
result = []for activation in act_func:print('\nTraining with -->{0}<-- activation function\n'.format(activation))
model = build_cnn(activation=activation,
dropout_rate=0.2,
optimizer=Adam(clipvalue=0.5))
history = model.fit(x_train, y_train,
validation_split=0.20,
batch_size=128, # 128 is faster, but less accurate. 16/32 recommended
epochs=100,
verbose=1,
validation_data=(x_test, y_test))
result.append(history)
K.clear_session()del model
print(result)
基于此,,我們可以為每個激活函數(shù)繪制從 model.fit() 得到的歷史圖,然后看看損失和準確度結(jié)果的變化情況,。
現(xiàn)在我們可以為數(shù)據(jù)繪圖了,,我用 matplotlib 寫了一小段代碼:
new_act_arr = act_func[1:]
new_results = result[1:]def plot_act_func_results(results, activation_functions = []):
plt.figure(figsize=(10,10))
plt.style.use('dark_background')# Plot validation accuracy valuesfor act_func in results:
plt.plot(act_func.history['val_acc'])
plt.title('Model accuracy')
plt.ylabel('Test Accuracy')
plt.xlabel('Epoch')
plt.legend(activation_functions)
plt.show()# Plot validation loss values
plt.figure(figsize=(10,10))for act_func in results:
plt.plot(act_func.history['val_loss'])
plt.title('Model loss')
plt.ylabel('Test Loss')
plt.xlabel('Epoch')
plt.legend(activation_functions)
plt.show()
plot_act_func_results(new_results, new_act_arr)
這會得到如下圖表:


