0 引言

    無(wú)線傳感器網(wǎng)絡(luò)(Wireless Sensor Networks，WSNs)是一種分布式傳感網(wǎng)絡(luò),。WSNs中的傳感器通過(guò)無(wú)線方式通信,，可以與互聯(lián)網(wǎng)進(jìn)行有線或無(wú)線方式的連接進(jìn)而形成一個(gè)多跳的自組織網(wǎng)絡(luò)系統(tǒng)^[1],。由于其密集型和隨機(jī)分布等特點(diǎn)，被廣泛應(yīng)用于環(huán)境監(jiān)測(cè),、醫(yī)療護(hù)理,、目標(biāo)跟蹤及交通控制等領(lǐng)域^[2-4]。由于傳統(tǒng)傳感器節(jié)點(diǎn)部署的隨機(jī)性和盲目性,，使傳感器對(duì)目標(biāo)區(qū)域不能進(jìn)行有效合理的監(jiān)測(cè),，因此采用合理的傳感器部署方案成為WSNs應(yīng)用中首先要考慮的問(wèn)題。

    傳感器網(wǎng)絡(luò)優(yōu)化部署是一個(gè)多目標(biāo)優(yōu)化問(wèn)題,，一個(gè)水質(zhì)監(jiān)測(cè)系統(tǒng)要實(shí)現(xiàn)好的監(jiān)測(cè)效果需要對(duì)水質(zhì)傳感器進(jìn)行合理的部署,。目前，國(guó)內(nèi)外許多學(xué)者對(duì)WSNs的覆蓋部署進(jìn)行了深入的研究,，其問(wèn)題的關(guān)鍵是針對(duì)不同的水域情況,，通過(guò)采用適當(dāng)?shù)膬?yōu)化策略對(duì)特定區(qū)域的傳感器節(jié)點(diǎn)進(jìn)行部署，在保證傳感器覆蓋率最大化的條件下,，盡可能少地使用傳感器,，達(dá)到資源的有效利用。隨著群智能優(yōu)化算法的興起,，其越來(lái)越多地成為研究者關(guān)注的焦點(diǎn),。文獻(xiàn)[5]-[6]用果蠅算法和魚(yú)群算法對(duì)傳感器節(jié)點(diǎn)進(jìn)行優(yōu)化布局，并取得了不錯(cuò)的效果,；文獻(xiàn)[7]提出了采用加權(quán)因子調(diào)整的粒子群算法對(duì)傳感器節(jié)點(diǎn)進(jìn)行自適應(yīng)部署，但算法中參數(shù)值的設(shè)定需根據(jù)經(jīng)驗(yàn)值進(jìn)行設(shè)定,；文獻(xiàn)[8]采用混沌粒子群算法覆蓋優(yōu)化無(wú)線傳感器網(wǎng)絡(luò),，該算法的尋優(yōu)速度較快，但其仍舊沒(méi)有擺脫粒子群算法易陷入局部極值點(diǎn)的缺點(diǎn),；文獻(xiàn)[9]提出了基于改進(jìn)的蟻群算法優(yōu)化網(wǎng)絡(luò)節(jié)點(diǎn),，該方法局部搜索能力強(qiáng)，但搜索速度較慢,；文獻(xiàn)[10]提出了把萊維飛行和粒子群相結(jié)合的算法來(lái)優(yōu)化傳感器節(jié)點(diǎn),，該算法利用萊維飛行搜索的遍歷性大大提高了網(wǎng)絡(luò)的覆蓋率，克服了傳統(tǒng)粒子群算法容易陷入局部最優(yōu)的缺點(diǎn),；文獻(xiàn)[11]提出分布式布谷鳥(niǎo)算法在無(wú)線傳感器網(wǎng)絡(luò)布局優(yōu)化中的應(yīng)用,，證明了分布式布谷鳥(niǎo)算法在優(yōu)化時(shí)間上要強(qiáng)于粒子群算法，但優(yōu)化精度不高,；文獻(xiàn)[12]提出了一種可變參數(shù)的改進(jìn)CS算法,，提高了收斂的速度；文獻(xiàn)[13]提出了動(dòng)態(tài)適應(yīng)布谷鳥(niǎo)算法,，對(duì)布谷鳥(niǎo)的發(fā)現(xiàn)概率和搜索步長(zhǎng)進(jìn)行動(dòng)態(tài)調(diào)整,，使得算法的收斂速度和精度都得到了一定的改善,。

    本文布谷鳥(niǎo)算法中用布谷鳥(niǎo)個(gè)體作為單個(gè)傳感器，模擬雛鳥(niǎo)不被寄主發(fā)現(xiàn)的過(guò)程,，將無(wú)線傳感器網(wǎng)絡(luò)中覆蓋率作為優(yōu)化目標(biāo),，布谷鳥(niǎo)優(yōu)勝劣汰的過(guò)程是一個(gè)不斷迭代，用好的可行解取代較差可行解的過(guò)程,，因此,，在這個(gè)過(guò)程中可以引入梯度下降求局部最優(yōu)解的方法。本文通過(guò)采用動(dòng)量梯度下降法,、均方根算法,、Adam優(yōu)化算法等深度學(xué)習(xí)中常用的優(yōu)化算法的思想，通過(guò)更新節(jié)點(diǎn)的位置快速計(jì)算每次迭代的最優(yōu)解,，能夠有效提高問(wèn)題的優(yōu)化效率,。

1 水質(zhì)傳感器網(wǎng)絡(luò)覆蓋模型

    在水質(zhì)傳感器網(wǎng)絡(luò)覆蓋中，通常通過(guò)增加傳感器個(gè)數(shù)以提高覆蓋率,。然而傳感器節(jié)點(diǎn)個(gè)數(shù)過(guò)多,，會(huì)產(chǎn)生大量冗余節(jié)點(diǎn)，造成數(shù)據(jù)傳輸沖突,，影響網(wǎng)絡(luò)穩(wěn)定性,，且造成資源浪費(fèi)。因此,，在水質(zhì)傳感器網(wǎng)絡(luò)布局階段,，節(jié)點(diǎn)數(shù)目和網(wǎng)絡(luò)覆蓋率需要同時(shí)考慮。

    本文在監(jiān)測(cè)水域的二維平面內(nèi),，運(yùn)用布谷鳥(niǎo)算法對(duì)節(jié)點(diǎn)自行進(jìn)行布置,，以實(shí)現(xiàn)對(duì)固定區(qū)域內(nèi)最大覆蓋率為目標(biāo)，在保證監(jiān)測(cè)數(shù)據(jù)有效的前提條件下,，使傳感器資源得到進(jìn)一步的利用,。假設(shè)每個(gè)傳感器都有相同的通信半徑和感知半徑^[14]，設(shè)s={s₁,，s₂,，s₃，…,，s_n}是一組無(wú)線傳感器集合,，(x_i，y_i)為集合中任意一個(gè)無(wú)線傳感器節(jié)點(diǎn)si的坐標(biāo),，(x_j,，y_j)為監(jiān)測(cè)區(qū)域中任意一點(diǎn)p_j的坐標(biāo)，則節(jié)點(diǎn)s_i到點(diǎn)p_j的歐氏距離定義為：

2 算法設(shè)計(jì)

    布谷鳥(niǎo)搜索(Cuckoo Search，CS)算法是由英國(guó)學(xué)者Yang于2009年受布谷鳥(niǎo)巢寄生育雛行為的啟發(fā)提出的一種新型的群智能優(yōu)化算法,。CS算法通過(guò)模擬布谷鳥(niǎo)巢寄生育雛行為,，結(jié)合鳥(niǎo)類(lèi)、果蠅等的Lévy飛行機(jī)制進(jìn)行尋優(yōu)操作,，能夠快速有效地找到問(wèn)題的最優(yōu)解,。CS算法的關(guān)鍵參數(shù)僅為外來(lái)鳥(niǎo)蛋被發(fā)現(xiàn)的概率和種群數(shù)目，整個(gè)算法操作簡(jiǎn)單,、易于實(shí)現(xiàn),。CS算法利用Lévy飛行進(jìn)行全局搜索，具有良好的全局尋優(yōu)能力,。

    為了模擬布谷鳥(niǎo)尋窩的方式,，需要設(shè)定一下3種理性的狀態(tài)：

    (1)每只布谷鳥(niǎo)每次隨機(jī)選擇一個(gè)巢并且產(chǎn)生一個(gè)卵；

    (2)在隨機(jī)選擇的一組寄生巢中,，最好的寄生巢將會(huì)被保留到下一代,；

    (3)可利用的寄生巢數(shù)量是固定的，寄生巢的主人能發(fā)現(xiàn)一個(gè)外來(lái)鳥(niǎo)蛋的概率為P_a,。

    布谷鳥(niǎo)算法中使用D維向量X=[X₁,，X₂，…,，X_D]表示每一個(gè)布谷鳥(niǎo),，結(jié)合了全局搜索的隨機(jī)游走和局部的隨機(jī)游走，其中,，全局搜索的隨機(jī)游走如式(5)所示：

其中,，r是縮放因子，是(0,，1)區(qū)間內(nèi)的隨機(jī)數(shù),；X_g，i,，X_g，k表示g代的兩個(gè)隨機(jī)數(shù),。CS算法流程如下：

    (1)初始化種群,，用每一個(gè)D維向量代表一個(gè)巢穴，同時(shí)計(jì)算出每個(gè)個(gè)體的適應(yīng)度,。

    (2)更新每個(gè)巢穴,，按照式(9)產(chǎn)生新的解，產(chǎn)生的新解比原來(lái)的解好,，則用新解替代舊解,。

    (3)對(duì)每個(gè)巢穴，任選其他兩個(gè)不一樣的巢穴,，對(duì)D維向量中的每個(gè)元素按照式(11)進(jìn)行組合產(chǎn)生新解,，產(chǎn)生的新解比原來(lái)的解好,，則用新解替代舊解。

    (4)記錄整個(gè)過(guò)程中的最優(yōu)解,，得到的最優(yōu)解不滿足設(shè)定的條件時(shí)返回步驟（2),，直到滿足條件或達(dá)到最大迭代次數(shù)則返回最優(yōu)解。

    在布谷鳥(niǎo)算法中影響布谷鳥(niǎo)尋優(yōu)效率的是Lévy飛行步長(zhǎng)控制量的選擇和淘汰概率,，本文基于深度學(xué)習(xí)優(yōu)化算法的思想來(lái)更新其參數(shù),。

3 基于深度學(xué)習(xí)的優(yōu)化算法更新Lévy飛行步長(zhǎng)

    在深度學(xué)習(xí)中，為解決目標(biāo)函數(shù)的最小值,，常用梯度下降法進(jìn)行優(yōu)化,，其基本思想是在每次迭代中，對(duì)每個(gè)變量,，按照目標(biāo)函數(shù)在該變量梯度的相反方向,，更新對(duì)應(yīng)的參數(shù)值，如式(12)所示：

其中,，J(θ)表示損失函數(shù),，η表示學(xué)習(xí)率，其決定了在沿著讓目標(biāo)函數(shù)下降最大的方向上,，下降的步長(zhǎng)有多大,。

    本文根據(jù)動(dòng)量梯度下降法(Gradient Descent with Momentum)、均方根算法(Root Mean Square prop)和Adam優(yōu)化算法(Adam Optimization Algorithm)來(lái)更新布谷鳥(niǎo)算法中Lévy飛行的步長(zhǎng),。

3.1 動(dòng)量梯度下降法

    動(dòng)量梯度下降法的基本思想是計(jì)算梯度的指數(shù)加權(quán)平均數(shù),，并利用該梯度更新權(quán)重，如式(13)所示：

式中,，V_dw是速度更新的大小,，β₁是權(quán)重，V_t-1是t-1時(shí)刻的速度,，V_t是當(dāng)前時(shí)刻速度的大小,，η是動(dòng)量梯度下降中的學(xué)習(xí)率。

    布谷鳥(niǎo)算法中Lévy飛行步長(zhǎng)更新采用動(dòng)量梯度下降法的思想,，即每次步長(zhǎng)的更新由前一步的步長(zhǎng)變化和當(dāng)前階段的步長(zhǎng)變化共同來(lái)決定,，如式（14）所示：

其中，Δl是步長(zhǎng)更新的大小,，Δl_t-1是前一個(gè)時(shí)刻步長(zhǎng)的更新,，η是步長(zhǎng)更新的學(xué)習(xí)率。

3.2 均方根算法

    均方根算法的基本思想是在梯度下降中,，想緩解縱軸方向的學(xué)習(xí)率,，然后加速橫軸方向的學(xué)習(xí)率，則采用式(15)所示的微分平方的加權(quán)平均數(shù)，使下降速度變快,。

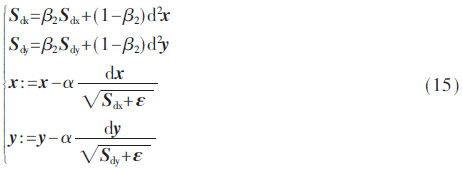
其中,，S_dx為x方向上的速度變化，S_dy為 y方向上的速度變化,，β₂是均方根中的權(quán)重,，α是均方根算法中的學(xué)習(xí)率，ε是一個(gè)防止分母為零的十分小的正向量矩陣,。通過(guò)改變S_dx和S_dy的大小來(lái)改變其在某一方向上的尋優(yōu)速度,。

    本文布谷鳥(niǎo)算法中Lévy飛行步長(zhǎng)更新采用均方根算法的思想，如式(16)所示：

其中,，S_dxy表示循環(huán)中每個(gè)個(gè)體到種群最優(yōu)位置距離的平均值,，X_g是尋優(yōu)中的每個(gè)個(gè)體位置，X_best是種群的最優(yōu)位置,。 

3.3 Adam優(yōu)化算法

    Adam優(yōu)化算法基本上是將動(dòng)量梯度下降法和均方根算法結(jié)合在一起,，且要加上修正偏差。本文布谷鳥(niǎo)算法中Lévy飛行步長(zhǎng)更新采用Adam優(yōu)化算法的思想,，如式(17)所示：

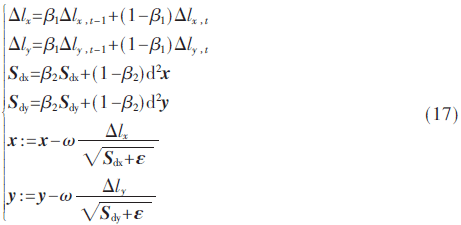
式中,，ω為Adam中的學(xué)習(xí)率。由式(17)可以看出在Adam優(yōu)化算法中采用了動(dòng)量梯度下降法的優(yōu)點(diǎn),，使得在尋優(yōu)過(guò)程中可以跳出局部最優(yōu)解,，同時(shí)也吸收了均方根算法的優(yōu)點(diǎn)，加快了在尋優(yōu)方向上的搜尋步長(zhǎng),，減少了不利的擾動(dòng)對(duì)尋優(yōu)過(guò)程造成的影響,。

4 更新淘汰概率P_a

    在梯度下降法尋找最優(yōu)值的過(guò)程中，因?yàn)樵胍舻拇嬖?，隨著迭代次數(shù)的增加,，結(jié)果會(huì)在最優(yōu)解的附近擺動(dòng)，不會(huì)精確地收斂,，此時(shí)的學(xué)習(xí)率是個(gè)固定值,，因此需要隨著迭代次數(shù)的增加慢慢減少學(xué)習(xí)率。

    在本文布谷鳥(niǎo)算法的改進(jìn)中淘汰概率P_a利用梯度下降的思想,，隨迭代次數(shù)的變化如式(18)所示：

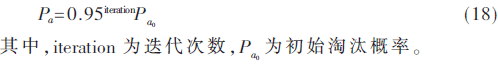
5 仿真結(jié)果

5.1 實(shí)驗(yàn)設(shè)計(jì)

    本文采用基于深度學(xué)習(xí)的優(yōu)化方法改進(jìn)布谷鳥(niǎo)算法對(duì)傳感器節(jié)點(diǎn)在監(jiān)測(cè)區(qū)域內(nèi)進(jìn)行網(wǎng)絡(luò)覆蓋率的最優(yōu)部署,，在100 m×100 m的水域內(nèi)，以2 m為邊長(zhǎng)劃分網(wǎng)格計(jì)算覆蓋率,。設(shè)定傳感器半徑為10 m，最大迭代次數(shù)為1 000,，初始淘汰概率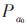設(shè)為0.25,，β₁設(shè)置大小為0.1，β₂設(shè)置大小為1，ε設(shè)為10^-4,，在本文算法中步長(zhǎng)控制量以及淘汰概率P_a隨迭代次數(shù)變化,。迭代計(jì)算中，當(dāng)?shù)螖?shù)大于最大迭代次數(shù)時(shí)跳出循環(huán),，則計(jì)算停止,，保存最優(yōu)結(jié)果退出布谷鳥(niǎo)更新過(guò)程。

5.2 實(shí)驗(yàn)結(jié)果與分析

    實(shí)驗(yàn)中隨機(jī)生成30個(gè)傳感器節(jié)點(diǎn),，圖1為原始的傳感器隨機(jī)分布圖,，X、Y為二維平面的橫縱坐標(biāo),。由圖1可以看出,，原始的傳感器分布比較雜亂，在隨機(jī)分配傳感器的條件下,，其覆蓋率比較低,只有59.64%,，實(shí)際工作中無(wú)法達(dá)到預(yù)期的監(jiān)測(cè)結(jié)果。

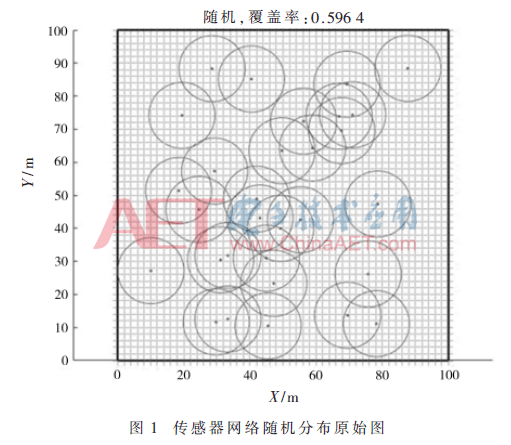
    圖2為在隨機(jī)分布傳感器節(jié)點(diǎn)的條件下,，節(jié)點(diǎn)通過(guò)基于Adam算法改進(jìn)的布谷鳥(niǎo)算法Adam-CS迭代更新之后的最優(yōu)位置分布圖,，在此分布條件下傳感器的覆蓋率達(dá)到最優(yōu)。從圖2中可以看出,，優(yōu)化后的傳感器節(jié)點(diǎn)分布比較均勻,，傳感器的重合度降低，覆蓋率達(dá)到86.48%,，進(jìn)而使得水質(zhì)傳感器節(jié)點(diǎn)部署得到優(yōu)化,，可有效提高傳感器網(wǎng)絡(luò)的監(jiān)測(cè)性能。

    圖3為原始布谷鳥(niǎo)算法（CS）,、基于動(dòng)量梯度下降法改進(jìn)的布谷鳥(niǎo)算法（Momentum-CS）,、基于均方根算法改進(jìn)的布谷鳥(niǎo)算法（RMSprop-CS）以及Adam-CS 4種方法的實(shí)驗(yàn)對(duì)比圖。在相同的區(qū)域面積部署相同數(shù)量及大小的傳感器節(jié)點(diǎn),?？紤]到隨機(jī)部署的不確定性對(duì)實(shí)驗(yàn)結(jié)果的影響，對(duì)4種方法各進(jìn)行了10次實(shí)驗(yàn),，對(duì)實(shí)驗(yàn)結(jié)果做均值處理,。由圖3可知，在相同的初始條件下,，Adam-CS算法可以更有效地提高網(wǎng)絡(luò)的部署效果,。隨著迭代次數(shù)的增加，4條曲線趨于平衡,，規(guī)定每增加30次迭代次數(shù)覆蓋率增長(zhǎng)少于0.05%的情況下為曲線達(dá)到的平衡狀態(tài),，則4種方法的結(jié)果如表1所示,。可見(jiàn),，Adam-CS算法可以利用更少的迭代次數(shù)實(shí)現(xiàn)更好的部署效果,。

6 結(jié)論

    本文基于深度學(xué)習(xí)的優(yōu)化方法改進(jìn)布谷鳥(niǎo)算法，以水質(zhì)傳感器網(wǎng)絡(luò)覆蓋率達(dá)到最優(yōu)為目標(biāo),，對(duì)傳感器節(jié)點(diǎn)進(jìn)行優(yōu)化部署,。在充分利用布谷鳥(niǎo)算法優(yōu)點(diǎn)的基礎(chǔ)上，對(duì)布谷鳥(niǎo)算法中的步長(zhǎng)控制量和淘汰概率利用深度學(xué)習(xí)的優(yōu)化方法進(jìn)行調(diào)整,，大大提高了算法的尋優(yōu)性能,。仿真結(jié)果表明，改進(jìn)后的算法能高效地搜索全局空間,，獲得更加精確的結(jié)果,，實(shí)現(xiàn)了深度學(xué)習(xí)方法和群智能優(yōu)化算法的結(jié)合，同時(shí)把改進(jìn)的算法應(yīng)用在水質(zhì)傳感器網(wǎng)絡(luò)的布局優(yōu)化中,，在水環(huán)境監(jiān)測(cè)中有一定的實(shí)踐意義,。

參考文獻(xiàn)

[1] 毛鶯池，陳力軍,，陳道蓄.無(wú)線傳感器網(wǎng)絡(luò)覆蓋控制技術(shù)研究[J].計(jì)算機(jī)科學(xué),，2007，34(3)：20-22.

[2] PUCCINELLI D,，HAENGGI M.Wireless sensor networks:applications and challenges of ubiquitous sensing[J].Circuits & Systems Magazine IEEE,，2005，5(3)：19-31.

[3] 徐凱,，張秋菊,，李克修，等.基于ZigBee的水產(chǎn)養(yǎng)殖無(wú)線監(jiān)控系統(tǒng)設(shè)計(jì)[J].電子技術(shù)應(yīng)用,，2012,，38(4)：67-69.

[4] 李建勇，李洋,，劉雪梅.基于ZigBee的糧庫(kù)環(huán)境監(jiān)控系統(tǒng)設(shè)計(jì)[J].電子技術(shù)應(yīng)用,，2016，42(1)：65-67.

[5] 霍慧慧,，李國(guó)勇.改進(jìn)的離散果蠅優(yōu)化算法在WSNs覆蓋中的應(yīng)用[J].傳感器與微系統(tǒng),，2016，35(2)：157-160.

[6] 何旭,，彭珍瑞,，董海棠，等.加權(quán)質(zhì)心魚(yú)群算法在WSNs節(jié)點(diǎn)優(yōu)化布置中的應(yīng)用[J].傳感器與微系統(tǒng),，2018,，37(10)：157-160.

[7] 余幸運(yùn),，孫茜，王小藝,，等.基于粒子群優(yōu)化算法的水質(zhì)傳感器優(yōu)化部署研究[J].傳感器與微系統(tǒng)，2016,，35(12)：30-32.

[8] 劉維亭,，范洲遠(yuǎn).基于混沌粒子群算法的無(wú)線傳感器網(wǎng)絡(luò)覆蓋優(yōu)化[J].計(jì)算機(jī)應(yīng)用，2011,，31(2)：338-340.

[9] 彭麗英.改進(jìn)的蟻群算法網(wǎng)絡(luò)節(jié)點(diǎn)覆蓋優(yōu)化研究[J].計(jì)算機(jī)仿真,，2011，28(9)：151-153.

[10] 盧玲,，謝佳華.萊維飛行的粒子群優(yōu)化算法在WSNs覆蓋增強(qiáng)中的應(yīng)用[J].傳感器與微系統(tǒng),，2015，34(11)：157-160.

[11] 劉小壘,，張小松.分布式布谷鳥(niǎo)算法在無(wú)線傳感器網(wǎng)絡(luò)布局優(yōu)化中的應(yīng)用[J].計(jì)算機(jī)應(yīng)用研究,，2018，35(7)：2063-2065.

[12] 王稼磊,，張會(huì)紅,，汪鵬君，等.基于參數(shù)自適應(yīng)布谷鳥(niǎo)算法的RM電路面積優(yōu)化[J].計(jì)算機(jī)應(yīng)用研究,，2018,，35(9)：135-137，141.

[13] 明波,，黃強(qiáng),，王義民，等.基于改進(jìn)布谷鳥(niǎo)算法的梯級(jí)水庫(kù)優(yōu)化調(diào)度研究[J].水利學(xué)報(bào),，2015,，46(3)：341-349.

[14] 劉偉，胡安林.無(wú)線傳感器網(wǎng)絡(luò)覆蓋率與節(jié)能性研究[J].電子技術(shù)應(yīng)用,，2016,，42(6)：98-100.

作者信息:

申志平，孫  茜,，王小藝,，許繼平，張慧妍,，王  立

（北京工商大學(xué) 計(jì)算機(jī)與信息工程學(xué)院,，北京100048）