放大電路的噪聲性能受到輸入電阻和反饋電阻 Johnson 噪聲(熱噪聲)的影響,。大多數(shù)人似乎都知道電阻會(huì)帶來(lái)噪聲,,但對(duì)于電阻產(chǎn)生噪聲的細(xì)節(jié)卻是一頭霧水。在討論運(yùn)放的噪聲前,,我們先做個(gè)小小的復(fù)習(xí):
電阻的戴維寧噪聲模型由噪聲電壓源和純電阻構(gòu)成,,如圖 1 所示。
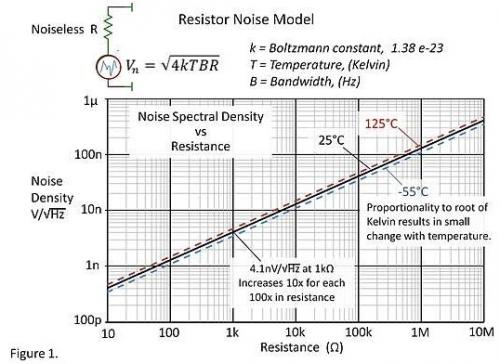
噪聲電壓大小與電阻阻值,,帶寬和溫度(開(kāi)爾文)的平方根成比例關(guān)系,。我們通常會(huì)量化其每 1Hz 帶寬內(nèi)的噪聲,也就是其頻譜密度,。電阻噪聲在理論上是一種“白噪聲”,,即噪聲大小在帶寬內(nèi)是均等的,在每個(gè)相同帶寬內(nèi)的噪聲都是相同的,。
總噪聲等于每個(gè)噪聲的平方和再開(kāi)平方,。我們常常提到的頻譜密度的單位是 V/。對(duì)于 1Hz 帶寬,,這個(gè)數(shù)值就等于噪聲大小,。對(duì)于白噪聲,頻譜密度與帶寬開(kāi)方后的數(shù)值相乘,,可以計(jì)算出帶寬內(nèi)總白噪聲的大小,。為了測(cè)量和量化總噪聲,,需要限制帶寬。如果不知道截止頻率,,就不知道應(yīng)該積分到多寬的頻帶,。
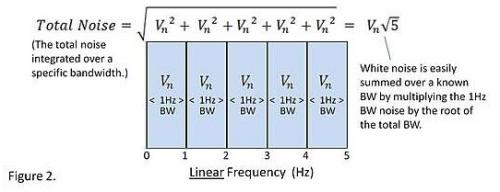
我們都知道頻譜圖是以頻率的對(duì)數(shù)為 x 軸的伯德圖。在伯德圖上,,同樣寬度右側(cè)的帶寬比左側(cè)要大得多,。從總噪聲來(lái)看,伯德圖的右側(cè)或許比左側(cè)更重要,。
電阻噪聲服從高斯分布,,高斯分布是描述振幅分布的概率密度函數(shù)。服從高斯分布是因?yàn)殡娮柙肼暿怯纱罅康男〉碾S機(jī)事件產(chǎn)生的,。中央極限定理解釋了它是如何形成高斯分布的,。交流噪聲的均方根電壓幅值等于高斯分布在±1σ范圍內(nèi)分布的振幅。
對(duì)于均方根電壓為 1V 的噪聲,,瞬時(shí)電壓在±1V 范圍內(nèi)的概率為 68%(±1σ),。人們常常認(rèn)為白噪聲和高斯分布之間有某種關(guān)聯(lián),事實(shí)上它們沒(méi)有關(guān)聯(lián),。比如,,濾波電阻的噪聲,不是白噪聲但仍然服從高斯分布,。二進(jìn)制噪聲不服從高斯分布,,但卻是白噪聲。電阻噪聲既是白噪聲也同時(shí)服從高斯分布,。
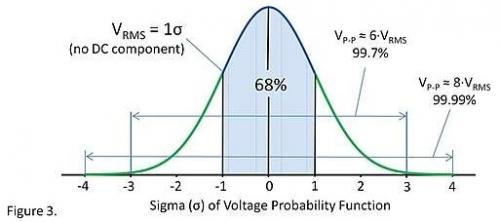
純理論研究者會(huì)認(rèn)為高斯噪聲并沒(méi)有定義峰峰值,,而它是無(wú)窮的。這是對(duì)的,,高斯分布曲線兩側(cè)是無(wú)限伸展的,,因此任何電壓峰值都是有可能的。實(shí)際中,,很少有電壓尖峰超過(guò)±3 倍的均方根電壓值,。許多人用 6 倍的均方根電壓值來(lái)近似峰峰值的大小。為了留有足夠的裕度,,甚至可以用 8 倍的均方根電壓值來(lái)近似峰峰值的大小,。
一個(gè)有趣的問(wèn)題是,兩個(gè)電阻串聯(lián)的噪聲之和等于這兩個(gè)電阻和的噪聲,。相似的,,兩個(gè)電阻并聯(lián)的噪聲之和等于這兩個(gè)電阻并聯(lián)后電阻的噪聲。如果不是這樣,,那么在串聯(lián)或者并聯(lián)電阻時(shí)就會(huì)出問(wèn)題,。還好它確實(shí)是這樣的,。
一個(gè)高阻值電阻不會(huì)因?yàn)樽陨碓肼曤妷憾a(chǎn)生電弧和火花。電阻的寄生電容并聯(lián)在電阻兩端,,將限制其帶寬和端電壓。相似的,,你可以想象絕緣體上產(chǎn)生的高噪聲電壓也會(huì)被其寄生電容和周?chē)膶?dǎo)體分流,。
一個(gè)有趣的測(cè)驗(yàn):對(duì)于一個(gè)開(kāi)路電阻,并聯(lián)一個(gè) 0.5pF 電容,,它的總噪聲是多少,?

